W kuźni i w bibliotece

31 października 2010
Marek Penszko

Po wycieczce w Pieniny postanowiłem wrócić na chwilę do kuźni Hefajstosa z przedpoprzedniego wpisu. Było w nim zadanie – niezbyt trudne, więc zdziwiły mnie jego nienajlepsze rozwiązania, zawarte w komentarzach paru łamiblogowych tuzów. Być może to efekt jakiejś „zmyłki” w treści zadania, której nie dostrzegam.
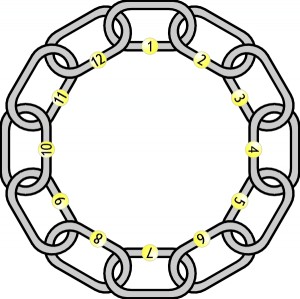
Przypomnę: należało rozciąć jak najmniej spośród 12 ponumerowanych ogniw łańcucha, tworzącego obrożę (pierścień)

tak, by po ich ponownym wpleceniu, ale w innych miejscach – powstała obroża, w której suma numerów na każdej parze połączonych ze sobą ogniw byłaby liczbą pierwszą.

Dziwne jest to, że kilka osób proponowało rozciąć aż cztery ogniwa: 2, 4, 8 i 10. Po tej operacji pierścień rozpada się na osiem kawałków:
(11-12-1) (-2-) (3) (-4-) (5-6-7) (-8-) (9) (-10-).
Nietrudno zrobić z nich „pierwszą” obrożę – rozwiązanie sprowadzi się wówczas na przykład do zamiany miejscami 2 z 10 i 4 z 8.

Szkopuł w tym, że ogniwa numer 2 rozcinać nie warto i nie należy – choćby dlatego, że jego umiejscowienie spełnia warunek „pierwszości”. Natomiast trzeba i wystarczy rozciąć po jednym ogniwie z każdej z trzech sąsiednich par, sumy numerów których nie są liczbą pierwszą, czyli
(4-5) (7-8) (10-11)
Jak się z tym uporać, podała w komentarzu Anka.
Po rozcięciu ogniw 4, 8 i 10 pierścień rozpada się na sześć części:
(11-12-1-2-3) (-4-) (5-6-7) (-8-) (9) (-10-),
z których można sklecić pierwszą „pierwszą” obrożę:
~1-2-3-4-9-10-7-6-5-8-11-12~
Jest też druga możliwość – rozcięcie ogniw 5, 7, 11; wówczas powstaną kawałki:
(12-1-2-3-4) (-5-) (6) (-7-) (8-9-10) (-11-)
a z nich pierścień:
~1-2-3-4-7-10-9-8-5-6-11-12~
Fragmenty wytłuszczone w obu rozwiązaniach można odwrócić.

Warto zwrócić uwagę, że rozcinane były albo tylko ogniwa o numerach parzystych albo nieparzystych. Dlaczego rozcięcie jednego nieparzystego i dwóch nieparzystych (lub odwrotnie) nie będzie skuteczne, czyli „pierwszej” obroży nie uda się wówczas zrobić – to temat do zgłębienia dla dociekliwych.
Wszystkich „pierwszych” pierścieni, które można utworzyć z liczb od 1 do 12 jest całkiem sporo – 512.

Przenieśmy się teraz z kuźni do biblioteki, pozostając jednak w temacie.
Na półce stoi osiem tomów Encyklopedii Łamigłówek, ale w kolejności niezgodnej z ich numeracją:

Trzeba je ustawić we właściwym porządku – od 1 do 8 (od lewej do prawej) – wykonując minimalną liczbę ruchów-przestawień. Każdy ruch polega na wyjęciu jednego tomu, przesunięciu kilku stojących na półce i wsunięciu wyjętego w nowe miejsce.
Ile ruchów wystarczy (i jakich), by tomy zostały ustawione jak należy?

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.