Tapa tip-top

11 lutego 2010
Marek Penszko

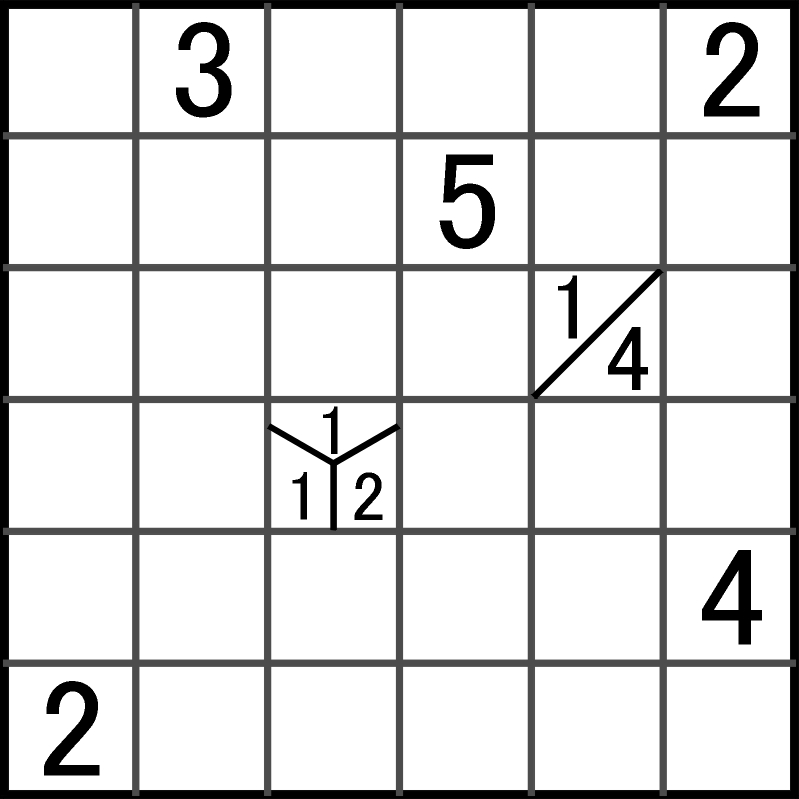
Turcy lansują tapę – łamigłówkę, rzec by można, narodową (TaPa = Turkish Puzzle). Oto przykład:

Część pustych pól należy zaczernić (w praktyce jakoś oznaczyć, np. kółkiem) tak, aby czarne pola tworzyły spójny obszar, czyli jeden wielokąt. Obszar ten nie może obejmować kwadratów 2×2 pola. Suma cyfr w danym polu oznacza, ile kratek, otaczających to pole, należy zaczernić. Jeśli cyfra jest jedna, to zaczernione pola powinny tworzyć jedną spójną grupę. Jeśli cyfr jest więcej, to spójnych grup powinno być tyle, co cyfr i mogą się one stykać tylko rogami; każda cyfra oznacza liczbę pól w innej grupie.
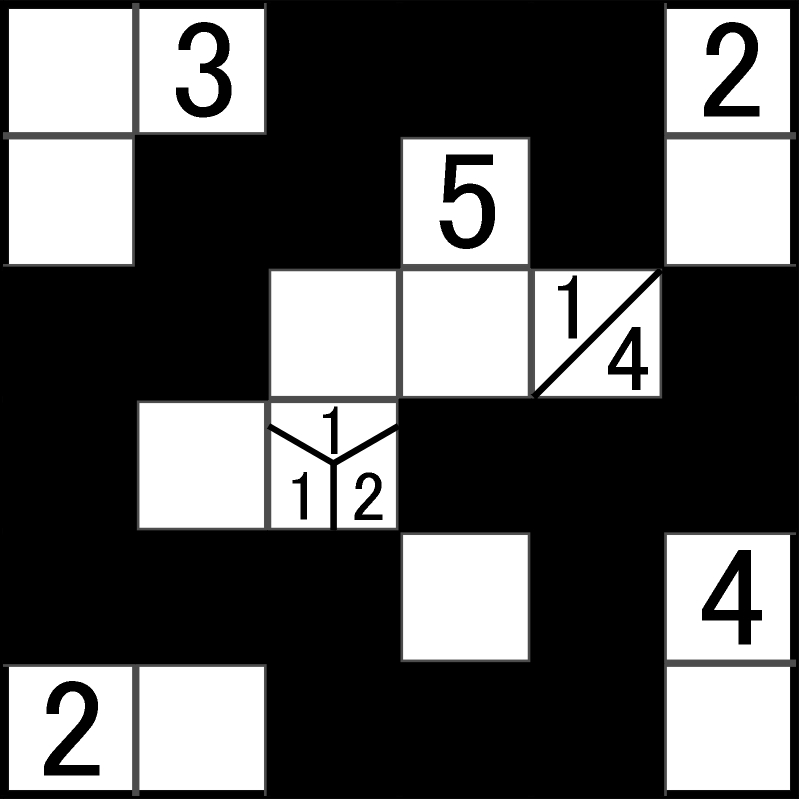
I rozwiązanie przykładu:

Turecka łamigłówka zasługuje na popularyzację. Jest pomysłowa, dość oryginalna i silna logicznie – taka w japońskim stylu, choć z tych bardziej wyrafinowanych, czyli raczej dla koneserów. Instrukcja obsługi może być w pierwszej chwili niejasna, ale przykładowy rysunek powinien rozwiać wątpliwości.

Choć tapa ma dopiero rok, obrasta już w odmiany i krzyżuje się z innymi łamigłówkami. Spora część tapowej rodzinki przedefilowała 6 lutego w ramach internetowego turnieju Tapa Variations Contest I. Niektóre okazy to zabawa zdecydowanie dla „nałogowców”. Osobiście chętniej rozparcelowałbym tapę. Inaczej mówiąc, od wymyślnych odmian wolę jej bardziej relaksowych protoplastów, którymi są przede wszystkim saper i nurikabe. W przypadku sapera przodkiem w linii prostej mogłaby być odmiana, którą nazywam zaporami minowymi, a która po raz pierwszy pojawiła się na mistrzostwach świata w Brnie w 2001 roku jako Worms, czyli robaki.

W odróżnieniu od tapy w rozwiązaniu powinny pojawić się trzy odrębne, spójne obszary – każdy w kształcie grubej linii łamanej (jak to robak) złożonej z 12 pól. W związku z tym wykluczone są nie tylko kwadraty 2×2, ale także rozgałęzienia linii-robaków; ponadto linie te nie tylko nie mogą się stykać, ale także żadna nie powinna dotykać samej siebie – nawet rogiem.
Przyznam się na koniec, że „utapiłem” robaki. W oryginale nie było pól z więcej niż jedną cyfrą, zastąpiłem więc jedną cyfrę dwoma lub trzema tam, gdzie mi robaki na to pozwoliły. Kto chciałby mieć większy zgryz, ten może robaki „odtapić”, czyli każdą grupkę małych cyfr zastąpić ich sumą. A gdyby byli Państwo tak mili i zechcieli pochwalić się rozwiązaniem, to interesowałoby mnie, ile razy robaki się zginają.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3 dni.