Równaj skok

8 lutego 2010
Marek Penszko

Dwa wpisy temu zamieściłem w konkursie dwa zadania szachowe z konikami polnymi. Ponieważ lubię „zakręcać” warunki konkursu związane z nagrodą, więc wymyśliłem, że przypadnie ona temu, kto nadeśle n-ty w kolejności komentarz z rozwiązaniem (rozwiązaniami), gdzie n jest sumą cyfr występujących w rozwiązaniach. Tymczasem z powodu mojej nieuwagi pojawił się feler – pierwsze zadanie (dwuchodówka) ma dwa rozwiązania, w których występują różne cyfry. A zatem n-te komentarze są dwa – dziesiąty (6 + 4) i dwunasty (8 + 4). Na szczęście hojny fundator wybawił mnie z kłopotliwej sytuacji, dorzucając drugą nagrodę, czyli grę Hive (Rój). Zabawne jest to, że autor dziesiątego komentarza (Andy) nadesłał rozwiązanie, które – gdyby było jedynym – wskazywałoby na autora dwunastego komentarza jako laureata, a w przypadku autora dwunastego komentarza (zuka) sytuacja jest dokładnie odwrotna. Obu komentatorów-laureatów proszę o kontakt (m.penszko@polityka.pl), czyli podanie adresów w celu przesłania nagród.

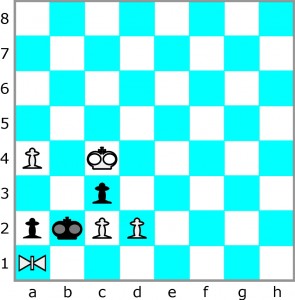
Konik polny ma kilku naśladowców. Najciekawszym i najczęściej pojawiającym się w bajkowych  zadaniach jest równoskoczek. Figura ta „działa” wzdłuż każdej linii prostej wyznaczonej przez dowolne dwa pola – A i B, a ściślej przez ich środki. A zatem nie tylko – mówiąc nieco po staroświecku – wertykalnie, horyzontalnie i diagonalnie, jak w przypadku hetmana, ale również na ukos pod innymi kątami. Ruch równoskoczkiem można wykonać tylko wówczas, gdy znajduje się na polu A, zaś na polu B stoi jakakolwiek inna bierka dowolnego koloru, a ponadto puste są pola między A i B oraz za B w odległości takiej, jaka jest między A i B. Ruch polega na przeskoczeniu przez B i stanięciu na polu C oddalonym od B o taki sam dystans, jaki jest między A i B. Inaczej mówiąc, A i C położone są symetrycznie względem B. Jeśli na C stoi bierka przeciwnika, zostaje zbita. W poniższym przykładzie równoskoczek (symbol – R; na diagramie znak przypominający kokardkę) ma pięć możliwości skoku z a1:

– na a3 przez a2,
– na c3 przez b2 (zbicie pionka),
– na e3 przez c2,
– na g3 przez d2,
– na e7 przez c4.
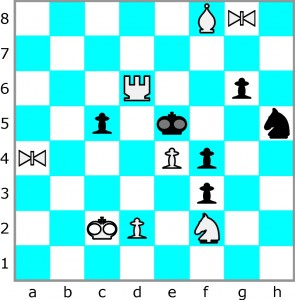
Kolej na dwuchodówkę z równoskoczkiem, a nawet dwoma. W rozwiązaniu wystarczy podać pierwszy ruch białych.

Zadanie jest trudne ze względu na tzw. złudy, czyli ruchy pozornie skuteczne, na które czarne mają ripostę, ale nie jest ona łatwa do znalezienia. Mam nawet wątpliwości, czy ktoś je rozwiąże (to nie prowokacja:)).
Dodatkowo zagadka mini: co wspólnego ma równoskoczek z gońcem?

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3 dni.