Wierzę w wieżę
Nasz Mistrz łamania głowy, Jan Mrozowski, podzielił się ze mną pewnym pomysłem zadania. Wpadł nań, myszkując w Łamiblogu, a ściślej, rozwiązując jedną z łamigłówek. Którą konkretnie, Mistrz nie podał, ale podejrzewam, że zamieszczoną we wpisie Armia Zera, bo jego dziełko jest podobne, czyli stanowi wariację na tematy wieżowe.
Zanim ów pomysł przedstawię (jeszcze nie tym razem), zacznę od wspomnianych tematów z wariacjami, których źródłem są rozważania dotyczące obchodzenia wieżą szachownicy – trasą wiodącą przez wszystkie pola, przez każde dokładnie raz.
Tras istnieje multum, a ich wyznaczanie jest trywialne, więc rozważania byłyby mało ciekawe, gdyby nie propozycja rzucania wieży kłód pod nogi.
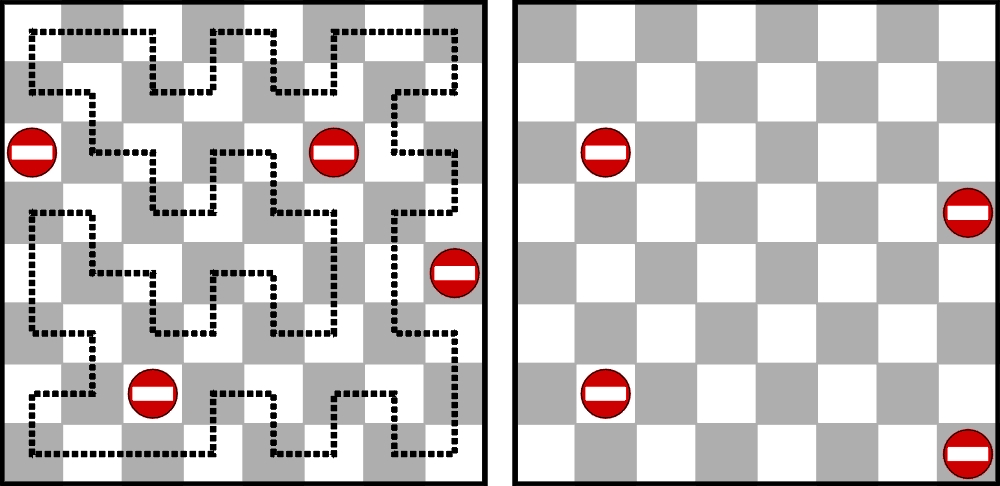
Na przykład: ile co najmniej pól szachownicy należy zablokować, czyli jakby usunąć z planszy, aby przez wszystkie pozostałe biegła tylko jedna trasa okrężna, czyli zamknięta? Okazuje się, że wystarczy skasować 4 pola. Znanych jest 15 całkowicie różnych sposobów rozmieszczenia blokad. Jeden z nich (z lewej) pochodzi z książki Łamigłówki. Podróże w krainę matematyki rekreacyjnej. W drugim unikalna trasa czeka na wyznaczenie.
Na pierwszy rzut oka może się wydawać, że duży obszar bez blokad umożliwia obejście 60 pól na wiele sposobów. W trakcie rozwiązywania szybko jednak okazuje się to złudnym wrażeniem.
Nietrudno dowieść, że każda z czterech blokad musi pojawić się w innej z narożnych ćwiartek (4×4) szachownicy; ponadto w centralnym kwadracie 4×4 nie może występować więcej niż jedna blokada. Jeśli te warunki nie będą spełnione, wówczas, aby zamknięta trasa była unikalna, trzeba wprowadzić dodatkowy warunek ograniczający jej przebieg. Oto łamigłówka z takim ekstra warunkiem.
Długość każdego fragmentu trasy między dwoma kolejnymi kropkami powinna być taka sama.
Na ilu polach umieszczony jest nakaz jazdy prosto, czyli trasa nie załamuje się (na trasie na rysunku z książki takich pól jest 8)?
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3 dni.

Komentarze
Zadanie 1. 9 pól
Zadanie 2. 18 pól
Dodanie kropek bardzo ułatwia rozwiązanie. Wystarczy wyliczyć odległości między kolejnymi kropkami (4 pola) i trasa wyskakuje prawie automatycznie. Zadania fajne, tylko mogłyby być trochę trudniejsze. Może ukryć jedno z pól z zakazem ? To tylko sugestia, nie wiem jak to by było w praktyce. Może ujawniać tylko niektóre pola z nakazem jazdy prosto i dwa (trzy) pola z zakazem wjazdu.
Wg mnie zadanie ma 2 rozwiązania – środek możemy połączyć na dwa sposoby (łącząc lewe/prawe i dolne/górne), a potem na lewą stronę mamy 2 możliwości.
Dzisiejsze lamiglowki nie byly super skomplikowane, moze dlatego ze nie wymagaly prawie zadnego liczenia (oprocz 60/12;)). Rozwiazania mozna zobaczyc tutaj:
http://pokazywarka.pl/ctec4c/
W drugiej lamiglowce nakaz jazdy prosto wystepuje na 26 polach.
Nakaz jazdy prosto występuje na 26 polach (5 poziomo i 21 pionowo).
Zadanie prościutkie. Wystarczy zauważyć, że od kropki do kropki przechodzimy w 5 krokach. Wynika to z tego, że wszystkich pól na trasie jest 60 a kropek mamy 12 i Długość każdego fragmentu trasy między dwoma kolejnymi kropkami powinna być taka sama.
Pozdrawiam
Witam.
Nakaz jazdy prosto umieszczony jest na 26 polach (34 pola to zakręty).
Witam
Ta druga trasa (z dodatkowym warunkiem) nie jest zbyt trudna. Znalazłem ją w pamięci (bez rysowania, jedząc śniadanie w biurze) i jeśli się nie pomyliłem w zliczaniu punktów bez zakrętu to jest ich 5. Wieczorem może podam samą trasę tylko musze wymyslić jak ją zaprezentować.
Tej pierwszej w samej pamięci nie zrobię. Ale już sobie zaczynam rysować.
pozdrawiam
peha
Pierwsza trasa składa się z 50 odcinków z długą na 8 pól prostą wzdłuż lewej krawędzi szachownicy.
pozdrawiam
peha
26 znaków
pzdr
Gdybym znalazł się w krainie absurdu, to bym powiedział, że zadanie ma 67108864 rozwiązania.
http://img69.imageshack.us/i/80893040.jpg/
Ale wizja 2 rozwiązań mnie przeraża…
Jak dobrze policzylem to 26 (około 10 minut zabawy).
Jazda prosto na 25 polach, ale to jest mało ciekawe. O wiele ciekawsze dla mnie jest stwierdzenie Psyho o możliwych 2 rozwiązaniach. Przez to stwierdzenie podchodziłem do tego prostego zadanka kilka razy i nie widzę drugiego rozwiązania – czekam na rozwiązania znalezione przez Psyho.
Po prostu i po prostym (rozwiazywaniu) – 26.
Stawiam kaktusa na dloni przeciw 2 rozwiazaniom Psyho.
Panie Marku, czy moglby Pan wczesniej uwolnic pelny komentarz Psyho, jesli sa w nim opisane dwa rozwiazania?
a
Andy:
OK, uwolnię jutro w samo południe.
m
Z ciekawości zrobiłem jeszcze raz – musiałem się walnąć i chyba nawet wiem gdzie (w lewym górnym rogu), aczkolwiek średnio pamiętam co napisałem 🙂
No w każdym razie teraz wychodzi mi jedno 🙂 Zakładam że w zadaniu w międzyczasie nic się nie zmieniło 🙂
Na drugiej planszy jest 10 takich pól, na trzeciej 26.
Na drugiej planszy droga prowadzi, zaczynając od lewego górnego rogu nast. 1p,1d,1p,1g,1p,1d,1p,1g,1p,1d,1p,1g,1p,2d,1l,1d,1l,1g,1l,1d,1l,1g,1l,1d,1l,2d,1p,1g,1p,1d,1p,1g,1p,1d,1p,1g,1l,2d,1l,1d,1l,1g,1l,1d,1l,1g,1l,1d,2l,7g.
Na trzeciej:1p,6d,1p,2g,1p,2g,1l,2g,1p,1d,1p,1g,1p,1d,1p,1g,1p,2d,2l,1d,1l,2d,1p,1d,1p,3g,1p,4d,3l,1g,1l,1d,3l,7g.
A jaka jest najmniejsza ilość blokad na planszy 9×9?
Michał:
na 9×9 potrzeba 7 blokad, aby trasa zamknięta była unikalna.
mp
Panie Marku,
wymienił Pan warunki jakie muszą być spełnione, aby po postawieniu 4 blokad było jedno rozwiązanie. Może warto dodać, że aby było choć jedno rozwiązanie, to koniecznym warunkiem jest postawienie blokad na dwóch białych i dwóch czarnych polach. Przy każdym innym ustawieniu zadanie nie ma żadnego rozwiązania.
Oczywiście wszystko to tyczy się kwadratowej szachownicy 8×8.
Pozdrawiam
Oczywiście Jazzie, można dodać.
A dlaczego tak być musi, drogie dzieci? Kto dowiedzie?
mp
łamana przechodzi na szachownicy kolejno z jednego koloru na drugi na zmianę. przy parzystej długości łamanej liczba pól jednego i drugiego koloru musi byc taka sama, proszę Pana:)
pozdr
Pafcio, piątka z plusem.
Koniec lekcji.
Następna jutro.
mp
Te 15 znanych rozmieszczeń blokad nie dawało mi spokoju. Takich rozmieszczeń jest co najmniej 24.
X0000000–X0000000–X0000000–X0000000
00000X00–000000X0–00000000–00000000
00000000–00000000–000000X0–000000X0
00000000–00000000–00000000–00000000
00000000–0000000X–00000000–00000000
00000000–00000000–000000X0–00000000
00000X00–00X00000–00000000–00000X00
00X00000–00000000–00X00000–00X00000
X000X000–X000X000–X000X000–X000X000
00000000–00000000–00000000–00000000
00000000–00000000–00000000–00000000
00000000–00000000–00000000–00000000
00000000–00000000–00000000–00000000
X0000000–00X00000–000000X0–000000X0
00000000–00000000–0X000000–00000000
0000X000–0000X000–00000000–X0000000
00X00000–000X0000–000X0000–000X0000
00000000–000000X0–000000X0–000000X0
000000X0–00000000–00000000–00000000
00000000–00000000–00000000–00000000
00000000–00000000–00000000–00000000
00000000–0X000000–00000X00–00000000
0X000X00–000000X0–00000000–00X000X0
00000000–00000000–000X0000–00000000
00X00000–00X00000–00X00000–00X00000
00000X00–00000X00–00000X00–00000X00
00000000–00000000–00000000–00000000
00000000–00000000–00000000–00000000
00000000–00000000–00000000–00000000
X0000000–00X00000–000000X0–00000000
00000000–00000000–0X000000–0X000X00
0000X000–0000X000–00000000–00000000
00X00000–00X00000–00X00000–00X00000
000000X0–00000000–00000000–00000000
00000000–000000X0–000000X0–000000X0
00000000–00000000–00000000–00000000
X000000X–00000000–00000000–00000000
00000000–X0000000–00X00000–000000X0
00000000–00000000–00000000–0X000000
00000000–0000X000–0000X000–00000000
X000X000–X000X000–X0000000–X0000000
00000000–00000000–00000X00–00000X00
00000000–00000000–00000000–00000000
00000000–00000000–00000000–00000000
00000000–00000000–00000000–00000000
00000000–00000000–000000X0–00000000
0X000X00–00000X00–00000000–0X000000
00000000–X0000000–00X00000–0000X000
Dwa rozmieszczenia pokazane we wpisie też tu są, w dwóch ostatnich rzędach ( trochę obrócone).
Antyp:
Podziwiam 🙂
Posprawdzam 🙁
Pozdrawiam 🙂
mp
Można zobaczyć jak wyglądają wszystkie trasy
http://pokazywarka.pl/ldes80/
Porównam z tym, co
Poodkrywali
Poprzedni
Poszukiwacze 🙂
mp
Antypie, tak na pierwszy rzut oka: w ostatnim diagramie w drugim rzędzie można poprowadzić więcej niż jedną trasę.
Niestety, nie mam teraz czasu, by „trasować” wszystkie.
mp
Ja zawsze mam dużo czasu, ale niestety bardzo rzadko potrafię go mądrze wykorzystać.
Wytyczyłem wszystkie trasy do rozwiązań Antypa i dwa przykłady:
(2,5) (numer wiersza, numer kolumny), (3,5) są niejednoznaczne.
Siedziałem nad programem, który znajduje te układy 5 dni. Sprawdzałem wszystko ręcznie i jak widać z poprzednich komentarzy, gdzieś się walnąłem. Najgorsze jest to, że nie mogę znaleźć błędu, który w programie ewidentnie jest. Z tego wynika, że poprawnych układów może być więcej. Może ktoś się pokusi aby je znaleźć. Mnie to przerasta.
Antypie, uległem pokusie i sprawdziłem wszystkie, przedstawione przez Ciebie rozwiązania. Moim zdaniem każdy przedstawiony diagram jest unikalny i ma dokładnie jedno rozwiązanie.
Moim zdaniem można ogłosić, że „znanych jest 24 całkowicie różnych sposobów rozmieszczenia blokad”. Nie próbowałem szukać innych rozwiązań. Myślę, że gdyby takie były, to byś je przedstawił.
Pozdrawiam
Jazzie, Antyp w pokazywarce przedstawił 24 rozwiązania. Sprawdź diagram umieszczony w 2 wierszu i 5 kolumnie oraz diagram z 3 wiersza i 5 kolumny.
nie miałem sił:) na sprawdzenie wszystkich, ale (2,5) i (3,5) moim zdaniem ma unikalne rozwiązanie
pozdr
W rozwiązaniach w pokazywarce jest błąd. Te dwa wskazane przez Andrzeja i Marka są faktycznie złe. Wszystko poprawnie jest pokazane w pierwszym komentarzu. Licząc po kolei od góry w pierwszym komentarzu, powinny to być układy 7 i 15 (są błędnie pokazane w pokazywarce, przesunięte X-y). Dlatego wszyscy mieli rację tylko Pan Marek i Andrzej opierali się na danych z pokazywarki, a pozostali na pierwotnym komentarzu. Przepraszam za zamieszanie.
Przyznam, że czegoś nie rozumiem. U mnie, przedstawione przez Antypa 24 rozwiązania (każde rozwiązanie to diagram 8×8), ułożone są w sześciu wierszach i czterech kolumnach. Wiersze rozdzielone są odstępami a kolumny myślnikami. Zatem proszę o wyjaśnienie, gdzie jest piąta kolumna, o której mówi Andrzej?
Pozdrawiam
Jazzie, uwagi Andrzeja dotyczą układu diagramów w pokazywarce. Namiary na nią podał Antyp ca 10 komentarzy wcześniej.
mp
Dziękuję. Teraz już wiem o co tu chodzi. Nigdy nie korzystałem z przeglądarki. Spróbuję poznać jej możliwości – może się przydać.
Pozdrawiam