Plątokąty

1 października 2009
Marek Penszko

Zadania, w których głównym motywem są sumy i sumowanie, sprowadzają się często do układu k prostych równań z n niewiadomymi, gdzie n > k (zwykle znacznie większe), a rozwiązań należy szukać wśród liczb całkowitych. Szkielet łamigłówki stanowią więc mało rozrywkowe i niezbyt zachęcające równania diofantyczne, natomiast tym, co ją uatrakcyjnia, jest zwykle „opakowanie”. Z drugiej jednak strony możliwość sprowadzenia zadania do układu równań nie musi oznaczać, że taki zabieg jest konieczny, aby je rozwiązać. Z reguły należy więc szukać sposobu lub punktu zaczepienia, pozwalającego ominąć żmudne próby rachunkowe, które nie bardzo pasują do łamigłówek. Nietrudno o to w prezentowanych poprzednio krzewach liczbowych i kapsułkach. Możliwe jest także w przypadku plątokątów, które spopularyzowali przed 13 laty Holendrzy, umieszczając je w programie mistrzostw świata.

 

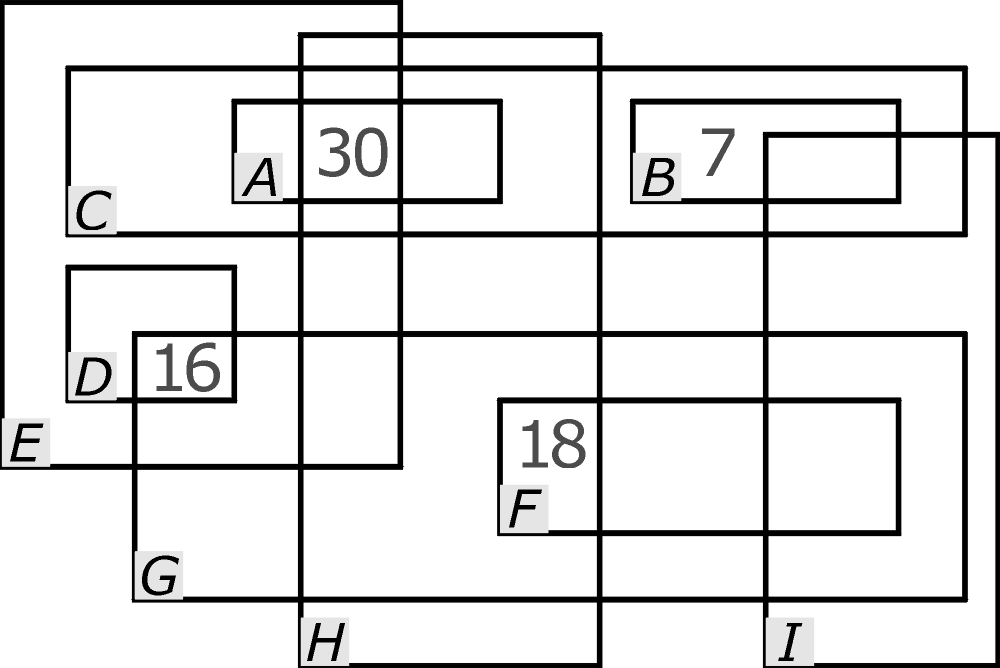
Każdemu prostokątowi przyporządkowana jest inna z liczb od 1 do 9. Liczby na rysunku oznaczają sumy wartości wszystkich prostokątów nakładających się na siebie w miejscu, gdzie umieszczona jest dana liczba. Jaka jest wartość każdego prostokąta?

Kilka lat później na turnieju w USA pojawiły się nieco inne plątokąty. Tak jak poprzednie, są również w pewnym stopniu testem spostrzegawczości, czyli warto poszukać miejsca, od którego najlepiej zacząć je rozgryzać.

 

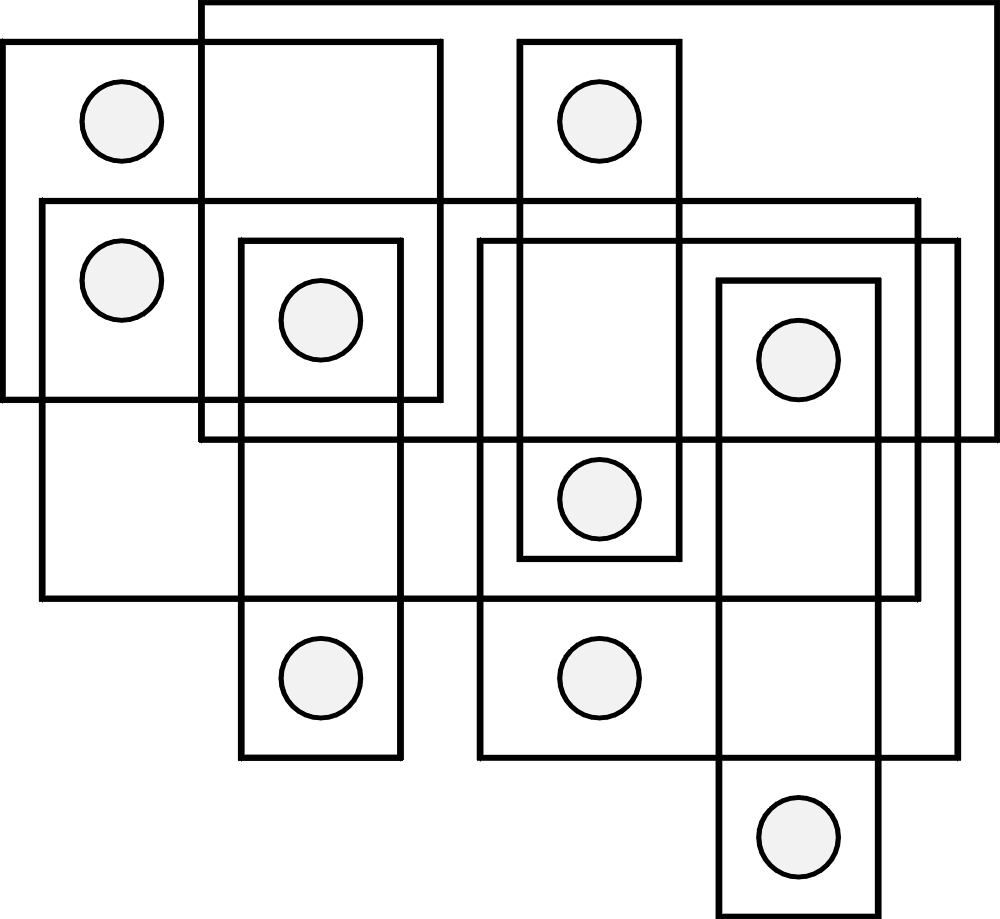
Do kółek należy wpisać dziewięć różnych liczb – od 1 do 9. Suma liczb w każdym prostokącie powinna być jednakowa.