Pustota kratek
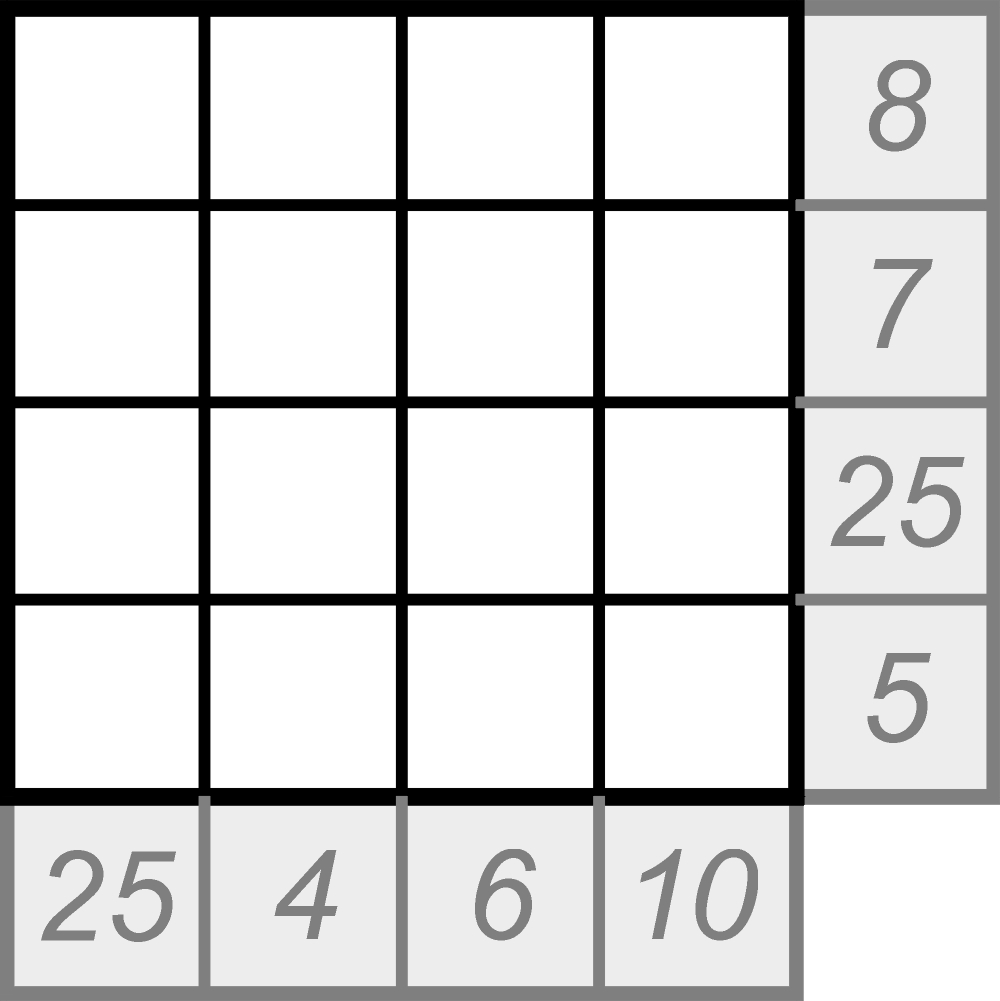
Jeśli w diagramie krzyżówki lub sudoku pozostaje choć jedno puste pole, to wiadomo, że jeszcze nie koniec, czyli jesteśmy w trakcie rozwiązywania. Zasada i nawyk wypełniania w podobnych zadaniach literami albo cyframi wszystkich kratek są tak silne, że pomysł, aby ograniczyć wpisywanie do niektórych kratek, można uznać za niemal obrazoburczy, niejako sprzeczny z naturą. Nie wiadomo, kto pierwszy na to wpadł. Oto przykładowe zadanie z takim „wybrykiem natury”, na pierwszy rzut oka przypominające survo z poprzedniego wpisu:
Każda liczba przy brzegu jest sumą liczb w kratkach w danym rzędzie lub kolumnie. Byłoby zatem survo, gdyby nie to, że suma sum (45) jest o wiele za mała, by dało się wcisnąć do wszystkich kratek liczby od 1 do 16. Jest natomiast dokładnie równa sumie liczb od 1 do 9 – i właśnie takie liczby powinny znaleźć się diagramie. Problem tylko w tym, która w której kratce. Problem tym większy – w porównaniu z survo – że siedem pól musi pozostać pustych, czyli jakby do wpisania jest dodatkowo siedem zer.
Im mniej liczb do ulokowania w diagramie i im większy diagram, tym trudniej ułożyć zgrabne zadanie z jednym rozwiązaniem. Aby było łatwiej, warto wspomóc się warunkiem dodatkowym. Przy obmyślaniu tego warunku inspiracją okazała się pewna gra typu papier-ołówek.
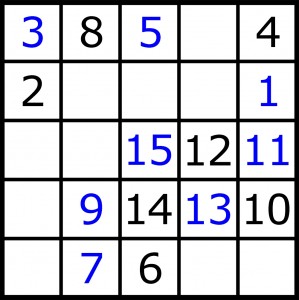
W polach kwadratu n x n (n>4) dwaj gracze umieszczają na przemian kolejne liczby naturalne. Każda następna powinna być wpisana w tym samym rzędzie lub kolumnie co poprzednia, a między nimi nie może być mniejszej liczby. Zwycięża, kto umieści ostatnią liczbę, czyli wpisanie następnej zgodnie z regułami nie będzie już możliwe. Poniżej przebieg przykładowej rozgrywki.
Po wpisaniu piętnastki „parzysty” poddał się (łatwo sprawdzić, że nie ma szans na zwycięstwo).
Czy gdyby przy brzegu diagramu wypisać sumy liczb znajdujących się w rzędach i kolumnach, można by jednoznacznie odtworzyć przebieg partii?
Kto spróbuje, ten potwierdzi, że jednoznacznie się nie da i nie będzie łatwo. Rozwiązywanie takich zadań ściśle na logikę jest zwykle żmudne i długotrwałe, czyli rozrywkowe inaczej. Aby było rozrywkowo normalniej, przydaje się intuicja, a ściślej zakładanie tego, co wydaje się najbardziej prawdopodobne. Na przykład, że do drugiej kolumny ładnie pasuje trójka kolejnych liczb – 7, 8, 9.
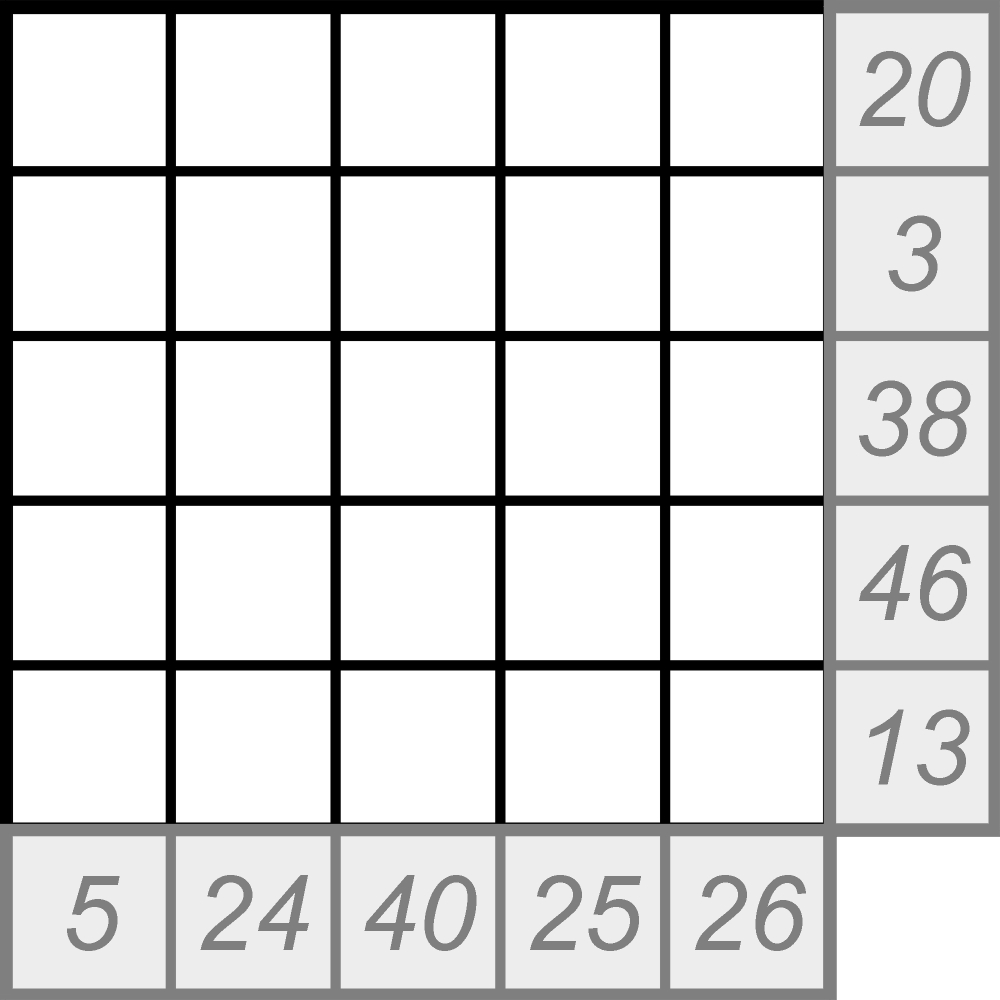
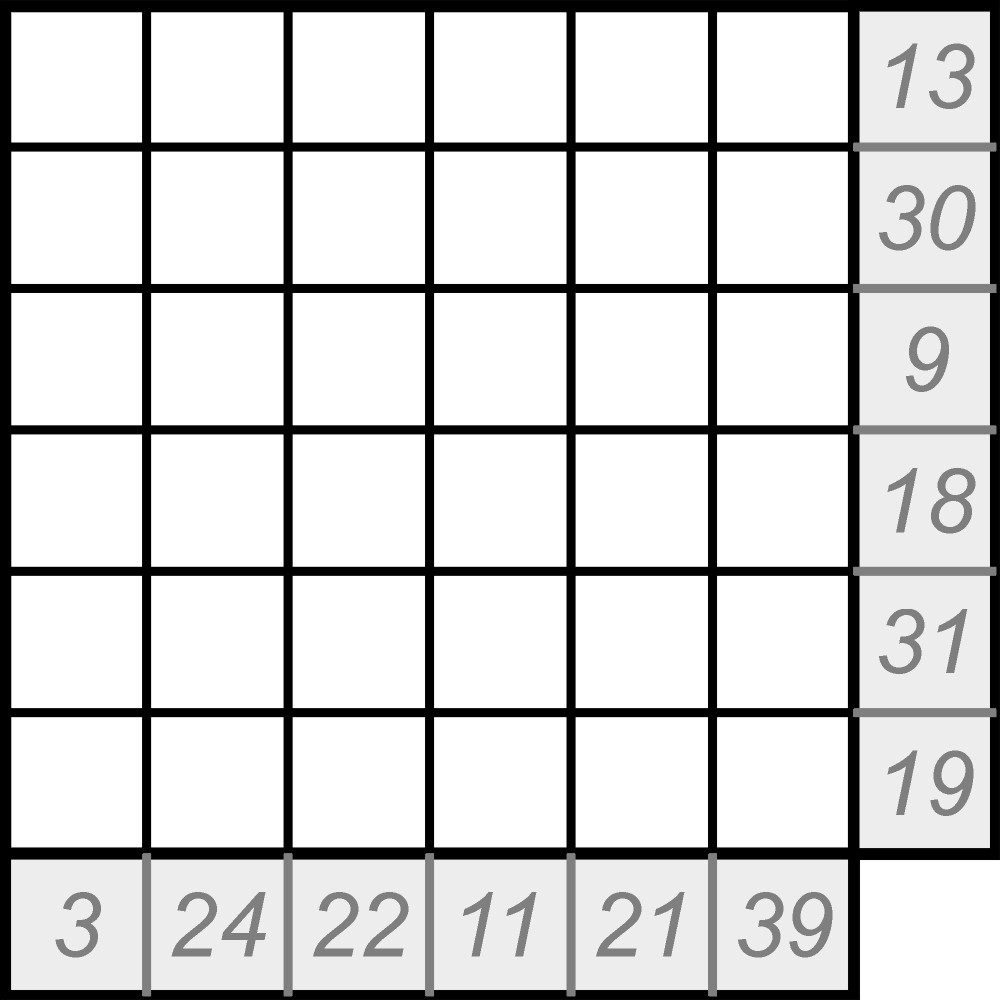
Takie częściowo „intuicyjne” zadania trafiają się nawet na łamigłówkowych mistrzostwach świata. Oto zapis innej partii opisanej wyżej gry – w postaci umieszczonych przy brzegach sum liczb w rzędach i kolumnach.
Diagram jest większy, ale – tak jak poprzednio – ostatnią umieszczoną w nim liczbą była piętnastka, którą wpisał nieopatrznie „nieparzysty” i natychmiast poddał się. Zadanie polega na odtworzeniu przebiegu partii, czyli rozmieszczenia wszystkich liczb, uwzględniając warunek dodatkowy: w każdym rzędzie (kolumnie) występują dwie lub trzy liczby – nie mniej i nie więcej.
Z tym zadaniem zmagali się uczestnicy 9. mistrzostw świata (Nowy Jork, 2000). Nie było lekko.

Komentarze
1.
8000
6010
9457
2003
A co do zadania ostatniego:
\7\6\\
1\15\\14
\\4 5\\
2\3\\13
\8\\11 12
\9\\10\
[mam nadzieję, że zrozumiałe]
Tego absolutnie nie jestem pewien – bo nie wydaje mi się, bym zrozumiał w całości zasady ;). Robiłem od końca przy dość dużym założeniu pt. 39=12+13+14.
Jest OK!
mp
Witam
Pierwszy przykład jest prosty. Wystarczy sprawdzić pary czterech cyfr o sumie 25 z jedną cyfrą wspólną. I później się samo rozwiązuje.
8,_,_,_
6,_,1,_
9,4,5,7
2,_,_,3
Natomiast to z mistrzostw z 2000 jest czasochłonne ale do rozwiązania. Chociaż na zawodach raczej bym z nim nie zdążył 😉
_,7,__,8,__,__
1,_,15,_,__,__
_,_,_4,5,__,__
2,_,_3,_,__,13
_,8,__,_,11,12
_,9,__,_,10,__
Pozdrawiam
peha
korekta rozwiązania
_,7,__,6,__,__
1,_,15,_,__,14
_,_,_4,5,__,__
2,_,_3,_,__,13
_,8,__,_,11,12
_,9,__,_,10,__
1.
8 X X X
6 X 1 X
9 4 5 7
2 X X 3
2. Na diagramie można spostrzec, że przełożenie dwóch par liczb (3,2) i (4,1) daje drugie rozwiązanie. Czyli, w tym przypadku umieszczenie przy brzegu diagramu sum liczb nie daje gwarancji jednoznaczności rozwiązania.
3.
X 7 X 6 X X
1 X 15 X X 14
X X 4 5 X X
2 X 3 X X 13
X 8 X X 11 12
X 9 X X 10 X
Wydaje mi się, że „nieparzysty”, gdzie by nie postawił piętnastkę, to i tak był już na straconej pozycji.
Kiedy przeczytałem dodatkowy warunek zadania, a ściślej mówiąc, jego część – „… nie mniej i nie więcej”, to od razu stanął mi przed oczami następujący obraz: http://www.youtube.com/watch?v=wKB9sEtDJOs&NR=1 (końcówka filmu).
Na początku zadanie wydawało mi sie typu „zgadnij i sprawdz” jedyne co pewno to to, że pierwsza kolumna ma ‚1’ i ‚2’, ale po dłuższej analizie udało się logicznie zadanie rozwiązać. Samo rozwiązywanie zajęło ze dwie minuty, ale wpatrywanie sie i wyciąganie wniosków z sum zajęło znacznie więcej czasu:) a to mi sie bardzo spodobało. choc juz po dobrym początku reszta zadania sama sie rozwiązuje. A oto moje rozwiązanie:
__,_7,__,_6,__,__
_1,__,15,__,__,14
__,__,_4,_5,__,__
_2,__,_3,__,__,13
__,_8,__,__,11,12
__,_9,__,__,10,__
Określenie typu zadań logicznych „zgadnij i sprawdź” – zabawne.
mp