Armia Zera
Cel uświęca środki. To a propos gry karcianej wydanej niedawno w Wielkiej Brytanii. Celem jest rozbudzenie popytu, a środkiem towarzysząca grze łamigłówka, za najlepsze rozwiązanie której zaoferowano 1000 funtów. Kwota nieoszałamiająca, zwłaszcza w porównaniu z dwoma milionami dolarów za ułożenie Eternity 2, ale wydawca też nie gigant – nowo powstała mała firma.
84 karty z obrazkami fantazyjnych wojowników przypominają modną przed laty wśród dzieciaków karciankę Pokemon. Do tego osiem kart określających rodzaj działań (atak lub obrona) i dwie kostki oraz opis reguł gry w… wojnę – nie całkiem losową i nie bardzo prostą, ale jednak adresowaną do dzieci lub mało wybrednych graczy. Tacy raczej nie rozwiążą łamigłówki za 1000 funtów, która, co by nie mówić, wygląda dość kusząco. Głównie dlatego, że jest jakoś ukryta wśród kart, więc przed rozwiązywaniem trzeba ją znaleźć. Nie jest to proste, bo o tym, czego się szuka, wiadomo niewiele. Z podpowiedzi wynika, że łamigłówkę tworzą jakieś układy kart oraz że jest ona 12- lub 13-częściowa, a każda z tych części jest sama w sobie łamigłówką. Podobno wystarczy mieć smykałkę do logiki i łamania szyfrów, aby uporać się z całością – do końca kwietnia przyszłego roku. Niestety, aby zainkasować nagrodę trzeba być obywatelem Zjednoczonego Królestwa. Zresztą dziesięciu funtów (tyle kosztuje karcianka) i tak bym w brytyjską Armię nie zainwestował, ale jednak bardzo jestem ciekaw rozwiązania.
Zwróciłem uwagę na Armię Zera przy okazji prezentowania indugadek, bo przypuszczałem, że związana z tą grą łamigłówka także ma charakter indukcyjny. Tymczasem okazało się, że to mieszanka – trochę indukcji, trochę dedukcji, a najwięcej intuicji i zgadywanki.
Natomiast znacznie bardziej indukcyjne propozycje zadań otrzymałem ostatnio od paru stałych gości Łamiblogu. Bardzo dziękuję za rozrywkę na deszczowe dni. Przynajmniej jedno z tych zadań, autorstwa Wiąza, wydało mi się warte zaprezentowania na blogu – właśnie w formie indugadki. Jest dość oryginalne, ciekawe i niezbyt trudne. A zatem najpierw przykład, na podstawie którego proszę ustalić zasady zabawy, a potem zwykła łamigłówka.
PS Osobę, która jako pierwsza uporała się z zadaniem kółkowo-krzyżykowym (z wpisu Orzeszek?), czyli Andy’ego, proszę o wybranie nagrody – gry Set!, 6. bierze lub Hive albo książki Łamigłówki. Podróże w krainę matematyki rekreacyjnej – oraz o podanie adresu, pod który ma być wysłana – jako komentarza do niniejszego wpisu (nie będzie ujawniony).

Komentarze
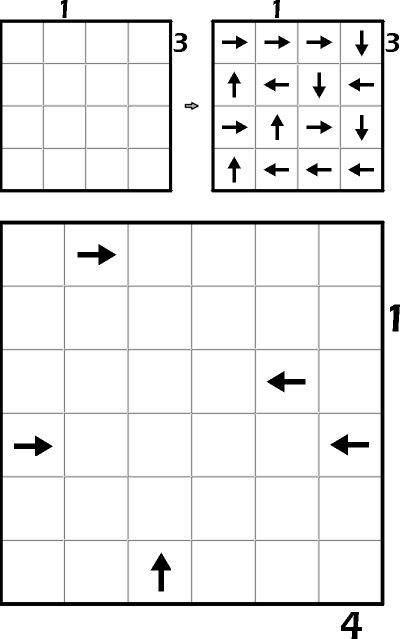
1) Strzalki tworza jeden zamkniety cykl.
2) Cyfra na brzegu oznacza ilosc strzalek, ktore „wskazuja” na miejsce tejze cyfry
D – dół, L – lewo, Prawo, Góra
PPPDPD
GDLPGD
GLGDLD
PPGDGL
GDLPPD
GLGLLL
Witam
zasady:
Liczby obok diagramu oznaczaja liczbę wskazujących je strzałek.
„Droga” wyznaczana przez strzałki powinna utworzyć zamkniętą, nieprzecinającą się pętlę, przechodzącą przez wszystkie pola diagramu.
rozwiązanie:
PPPDPD
GDLPGD
GLGDLD
PPGDGL
GDLPPD
GLGLLL
gdzie:
P – strzałka w prawo
L – strzałka w lewo
G – strzałka w górę
D – strzałka w dół
Pozdrawiam
peha
Cyfry na brzegach planszy mówią ile strzałek jest skierowanych w ich stronę w danym rzędzie lub kolumnie. Tor jaki wyznaczają strzałki musi tworzyć zamknięty obwód.
legenda:
p – strzałka skierowana w prawo
l – strzałka skierowana w lewo
g – strzałka skierowana w górę
d – strzałka skierowana w dół
Rozwiązanie:
pppdpd
gdlpgd
glgdld
ppgdgl
gdlppd
glglll
W diagramie należy umieścić strzałki (po jednej w każdej kratce) skierowane w górę, dół, prawo lub lewo. Zaczynając z dowolnego pola kierując się kolejno na sąsiednie pole wskazane przez strzałkę przejdziemy przez wszystkie pola diagramu i wrócimy do punktu startu. Liczby na zewnątrz diagramu wskazują ile strzałek w rzędzie/kolumnie wskazuje na tę liczbę.
Rozwiązanie: P-prawo, L-lewo, G-góra, D-dół.
PPPDPD
GDLPGD
GLGDLD
PPGDGL
GDLPPD
GLGLLL
„Jest dość oryginalne, ciekawe i niezbyt trudne.” – bardzo trafnie opisane zadanie.
A jego zasady? Należy zrobić „węża” (pętlę) wewnątrz planszy tak, aby wszystkie pola zostały zajęte. Strzałki wskazują kierunek ruchu miedzy polami, a liczby podpowiadają, ile strzałek w odpowiednim rzędzie lub kolumnie jest skierowanych w stronę tej liczby.
Rozwiązanie: (P- w prawo, G-do góry, itd…)
PPPDPD
GDLPGD
GLGDLD
PPGDGL
GDLPPD
GLGLLL
Ujawnionych strzałek jest w sam raz. Gdyby było mniej, to rozwiązań byłoby więcej
P P P D P D
G D L P G D
G L G D L D
P P G D G L
G D L P P D
G L G L L L
Litery zamiast strzałek wskazujących w Prawo, Lewo, Górę, Dół.
a
Niezłe strzałki tworzą jedną pętlę, liczby na bokach mówią ile strzałek pokazuje na tą liczbę.
strzałki tworzą jedną pętlę, liczby na bokach mówią ile strzałek pokazuje na tą liczbę.
P P P D P D
G D L P G D
G L G D L D
P P G D G L
G D L P P D
G L G L L L
EEESES
NSWENS
NWNSWS
EENSNW
NSWEES
NWNWWW
N – strzałka do góry
S – strzałka w dół
W – strzałka w lewo
E – strzałka w prawo
Strzałki muszą utworzyć pętlę. A liczby poza diagramem mówią ile strzałek wskazuje w tym kierunku.
pppdpd
gdlpgd
glgdld
ppgdgl
gdlppd
glglll
Jeśli się nie mylę, to liczby oznaczają, ile jest strzałek „wymierzonych w ich stronę”, czyli ile w danym wierszu lub kolumnie strzałek skierowanych jest w prawo, w lewo, w górę lub w dół, zależnie od tego, gdzie jest umieszczona liczba. Poza tym, idąc „po strzałkach” powinniśmy obejść wszystkie pola.