Wieczność trwa
Zakończył się pierwszy, trwający 1,5 roku etap układankowej zabawy Eternity 2, w której do wygrania były 2 miliony dolarów. I są nadal, bo do przełomu 2008/2009 nikt nie nadesłał prawidłowego rozwiązania.
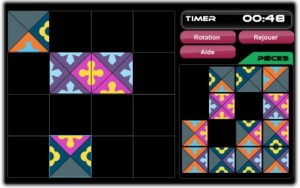
Krótko przypomnę: chodzi o ułożenie dużego kwadratu 16×16 z 256 małych kwadratowych płytek tak, aby brzegi stykających się płytek (takich miejsc jest 480) były wszędzie dopasowane jak należy – na obu powinien być taki sam wzór (kolor i kształt).
Organizator, brytyjski oddział firmy zabawkarskiej Tomy (to wy?), zagrał na nosie wszystkim, którzy potraktowali konkurs zbyt poważnie, przyznając „nagrodę pocieszenia” – 10 tysięcy dolarów – za… błędne rozwiązanie. I słusznie, łamigłówka nie jest dla garstki zakręconych programistów tylko dla rzeszy naiwnych klientów, którzy mają dużo czasu do stracenia i na których trzeba zarobić. Służą temu także cztery łamigłówki pomocnicze (początkowo były tylko dwie). Po uporaniu się z każdą (jedna kosztuje około 20 funtów) można spodziewać się podpowiedzi od organizatora, czyli wskazania położenia jednej płytki w rozwiązaniu. W sumie podpowiedzi można mieć pięć, bo jedna, przeznaczona dla wszystkich, znajduje się w głównej instrukcji. Warto pamiętać, że Eternity 2 jest dziełem tęgich matematycznych głów, których właściciele zarobią tym więcej, im dłużej układanka pozostanie niezłamana. Jasne, że musieli się bardzo starać, aby tak było do końca Wieczności. Nawet po uwzględnieniu wszystkich podpowiedzi liczba kwadratów możliwych do ułożenia jest kosmiczna – składa się z 546 cyfr. Dla porównania, liczba atomów tworzących część wszechświata, którą możemy obserwować ciężko uzbrojonymi zmysłami, to „tylko” 80 cyfr.
Organizatorzy postanowili nagrodzić wspomnianą kwotą jedną z osób, które zdecydowały się pochwalić, niejako poza konkursem, swoim osiągnięciem. Wybrano oczywiście tę, która była najbliżej celu. Padło na panią Annę Karlsson z Lundu. Szwedce nie pasowały w ułożonym kwadracie krawędzie w 13 miejscach. Teraz niejeden rozwiązujący, który miał lepiej, śle protesty do organizatorów, bo skąd mógł wiedzieć, jaka niespodzianka go ominie. Chwyt marketingowy zapewne okaże się skuteczny i można się spodziewać, że w drugim etapie (do końca br., ewentualny trzeci i ostatni etap przypadnie na rok 2010) sypnie rozwiązaniami bliższymi ideału, choć wcale nie ma pewności, że organizatorzy ponownie będą mieli gest. Formalnej zmiany w regulaminie, dotyczącej „nagrody pocieszenia”, nie wprowadzono. Nowicjusze, którzy nabrali smaku na Wieczność, mogą potrenować na stronie firmowej na 1/16 oryginalnej planszy.
W sumie na płytkach są 23 wzory krawędziowe, z czego jeden (szary) oznacza brzeg układanego kwadratu. Wiadomo więc, które 4 płytki należy umieścić w rogach, a które 56 na skrajach. W szaleństwie rozmieszczenia pozostałych 22 wzorów nie ma jednak żadnej metody poza tym, że każdy występuje parzystą liczbę razy. Wiele osób, które zdecydowało się na zakup Eternity II, zniechęca już przy pierwszym kontakcie wielkość planszy oraz liczba płytek. „Monstrualne” rozmiary dobrze oddaje rozwiązanie, które pojawiło się w Internecie jeszcze w 2007 roku jako prawidłowe.
Była to oczywiście mistyfikacja. Jej autor zamierzał zapewne zniechęcić konkurencję.
Wracając do wybrakowanego rozwiązania pani Karlsson, w informacji podanej oficjalnie przez firmę Tomy mowa jest o 13 niedopasowanych krawędziach. Czy można stąd wywnioskować, ile płytek pozostało nieułożonych, czyli ile co najmniej należałoby ich usunąć z pełnego kwadratu, aby wszystkie pozostałe krawędzie do siebie pasowały? Na pewno nie więcej niż 13 i nie mniej niż 4. Konkretną liczbę nie sposób ustalić, ale czy dałoby się określić, jaka jest najbardziej prawdopodobna?



Komentarze
Nie czytałem nawet instrukcji do Eternity, ale tak się zastanawiam czy to pewne, że szara krawędź oznacza brzeg kwadratu? Czy na przykład te narożniki nie mogą być w środku? Jest to jasno określone?
I jeszcze odnośnie rozwiązania Szwedki. Jedno z pytań brzmiało: „Czy można stąd wywnioskować, ile płytek pozostało nieułożonych”. Wydaje mi się, że jeśli przynajmniej jeden klocek jest ułożony źle (a jest ich co najmniej 4) możemy z prawdopodobieństwem ponad 0,99 stwierdzić, że co najmniej 254 klocki są źle ułożone (jeśli pewne są te dwa które są podpowiedziami z małych Eternity). A to, że pasują do siebie nie oznacza, że są na swoich miejscach. No jeszcze można narożniki zgadnąć w zależności czy zachodzi warunek z mojego pytania powyżej.
Orgu, ponieważ znani eternitolodzy nie zabierają głosu, więc poczułem się wywołany do tablicy.
Szarość na brzegu jest pewna – tak stoi w instrukcji.
Pytając o to, ile płytek Szwedka (najprawdopodobniej) ułożyła źle, miałem na myśli wyłącznie jej wybrakowane rozwiązanie, bez odnoszenia się do jakiegoś poprawnego wzorca. Inaczej mówiąc: płytka leży źle wtedy, jeśli wzór na przynajmniej jednym jej brzegu nie pasuje do wzoru na brzegu sąsiedniej płytki.
Przy okazji ciekawostka: organizatorzy znają oczywiście poprawne rozwiązanie, ale wcale nie ma pewności, czy nie znają takich rozwiązań kilku lub więcej, a ponadto twierdzą, że różnych poprawnych rozwiązań mogą być krocie, jak w przypadku Eternity 1.
Pozdrav
mp
Określenie najbardziej prawdopodobnej liczby nie pasujących płytek w rozwiązaniu Szwedki byłoby proste, gdyby dało się sprowadzić do następującego zadania.
W zbiorze cyfr od 1 do 4 każda cyfra występuje wielokrotnie i wyciagnięcie każdej jest tak samo prawdopodobne. Ze zbioru tego wyciągamy kolejno po jednej cyfrze. Wyciągnięcie jakiej liczby cyfr, których suma będzie równa 13, jest najbardziej prawdopodobne?
W takim przypadku odpowiedzią jest 7.
Jednak w przypadku Eternity sprawa jest bardziej skomplikowana i zależy od wielu innych czynników, także subiektywnych związanych ze sposobem układania płytek, więc prawdopodobieństwo można szacować raczej na wyczucie, niż w wyniku obliczeń.
a