Same wtręty

1 lipca 2009
Marek Penszko

Od krzyżowania słów do krzyżowania liczb droga krótka, więc tym drugim zaczęto się zabawiać tuż po spopularyzowaniu krzyżówek w połowie lat 20. ubiegłego wieku. Początkowo była to kalka zabawy słownej, czyli każdą liczbę odgadywano na podstawie jednego objaśnienia. Dopiero z czasem autorzy zauważyli, że splatanie liczb może być – inaczej niż słów – jakby podwójne, czyli nie tylko w diagramie, ale także w objaśnieniach. Dzięki temu zestaw objaśnień upodabnia się do układu równań – te same niewiadome występują w różnych objaśnieniach-równaniach. Krzyżówki liczbowe w takiej postaci gościły w poprzednich wpisach. Są moim zdaniem ciekawsze, ale dla porównania warto posmakować tej pierwszej formy – w stylu retro, która dziś czasem także się pojawia. Przypomina zresztą kakuro, jednak nie jest tak sztampowa, bo „podpowiedzi” nie są w niej ograniczone do sum cyfr.

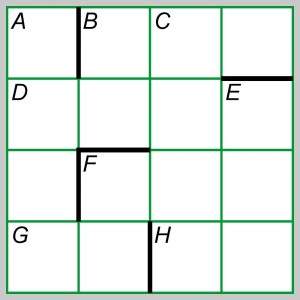
W krzyżówce zamieszczonej we wpisie „Nie tylko kakuro” wśród objaśnień był jeden wtręt w starym stylu (G pionowo – iloczyn dwu liczb pierwszych), na co słusznie, jako na zbędny dodatek, zwrócił uwagę w komentarzu Robert_C. W poniższym zadaniu wszystkie objaśnienia są takimi „wtrętami”.

Poziomo:
B) sześcian
D) wielokrotność jedenastu
F) kwadrat liczby pierwszej
G) liczba nieparzysta
H) suma pięciu kolejnych liczb całkowitych.
Pionowo:
A) każda następna cyfra jest o jeden mniejsza od poprzedniej
B) potęga
C) każda następna cyfra jest o jeden większa od poprzedniej
E) iloczyn trzech kolejnych liczb całkowitych
F) kwadrat.

Zabawa jest konkursowa. Termin nadsyłania rozwiązań – jako komentarzy do tego wpisu (komentarze z rozwiązaniami nie będą przed upływem terminu ujawniane) – 3 doby od pojawienia się wpisu. Nagrodę (gra 6. bierze! lub książka Łamigłówki. Podróże w krainę matematyki rekreacyjnej) wybierze osoba, która nadeśle N-te rozwiązanie. N jest liczbą dzielników sumy wszystkich szesnastu cyfr występujących w rozwiązaniu. Jako rozwiązanie wystarczy podać N.