Prosto z Prościejowa

12 lutego 2009
Marek Penszko

Jedni rozwiązują sudoku dla relaksu lub zabicia czasu, inni wyczynowo. To tak, jak w sporcie, który jest rekreacyjny lub kwalifikowany. Nie dotyczy to oczywiście wszystkich konkurencji. Nikt np. dla zabicia czasu nie rzuca młotem. Nie tylko czas mógłby paść ofiarą.

Niedzielnych rozwiązywaczy siermiężnego sudoku jest u nas jeszcze chyba sporo, skoro tytułów pisemek w większości nim zadrukowanych nadal nie brakuje, doliczyłem się aż dziewięciu – miesięczników lub „rzadszych”. Wyczynowców gustujących w mniej lub bardziej zakręconych, nieschematycznych odmianach znalazłoby się może parę setek. Bardzo wybrednego smakosza, który próbuje tylko tego, czego dotąd nie konsumował i co wygląda interesująco – znam jednego, bardzo osobiście.
Coraz rzadziej trafiam na coś zachęcającego do konsumpcji, ale na Czechów zawsze mogę liczyć. W styczniu zorganizowali duży turniej interentowy Sudokucup z udziałem niemal całej czołówki światowej. Z najlepszych zabrakło tylko aktualnego mistrza świata Thomasa Snydera i Jakuba Ondrouška. Impreza była starannie przygotowana (m. in. instrukcje w pięciu językach, także po polsku). Zwyciężył, jakżeby inaczej, nasz kandydat na mistrza świata Jan Mrozowski. Większość zadań była trudna, rodzaje mniej lub bardziej znane, ale smakowitego kąska nie zabrakło – przypomina trochę KenKen.

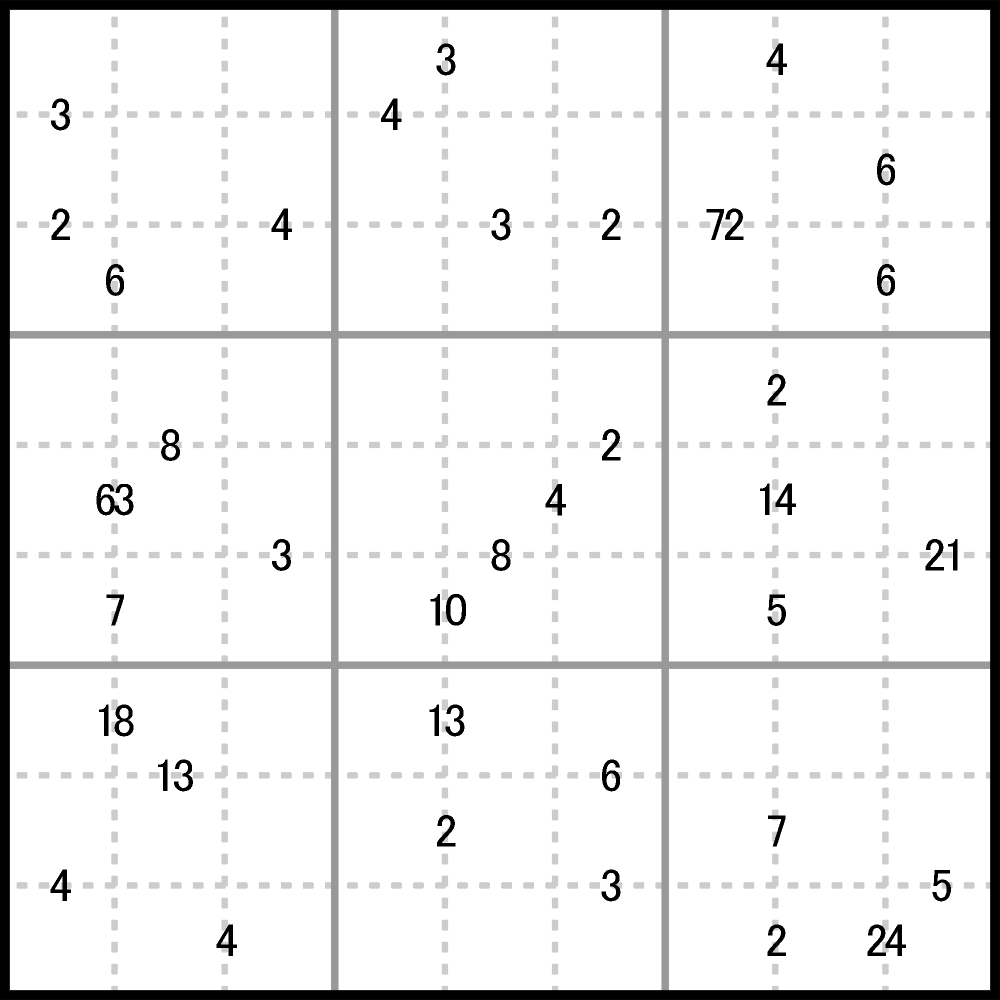
Mathdoku

W każdym sektorze (3×3) ujawniono cztery wyniki różnych działań (+, -, *, /) – zawsze na parze liczb, między którymi znajduje się wynik.

Poza tym u naszych sąsiadów trwa cykl turniejów Grand Prix (jego ukoronowaniem będą mistrzostwa w Brnie 29 marca; organizatorzy serdecznie zapraszają sudokowiczów z Polski). W jednym z nich, w Ostrawie, miałem przyjemność uczestniczyć, a najciekawsze zadania zaprezentowałem onegdaj w Łamiblogu tu i tu. 7 lutego odbył się kolejny – w Prościejowie, uroczym miasteczku na Morawach. Wśród zadań także znalazło się jedno urzekające oryginalnością pomysłu. Rozwiązywanie jest przyjemne, bo dzięki kółkom i krzyżykom można posmakować dodatkowych uroków wędrówki ścieżką logicznego wnioskowania.

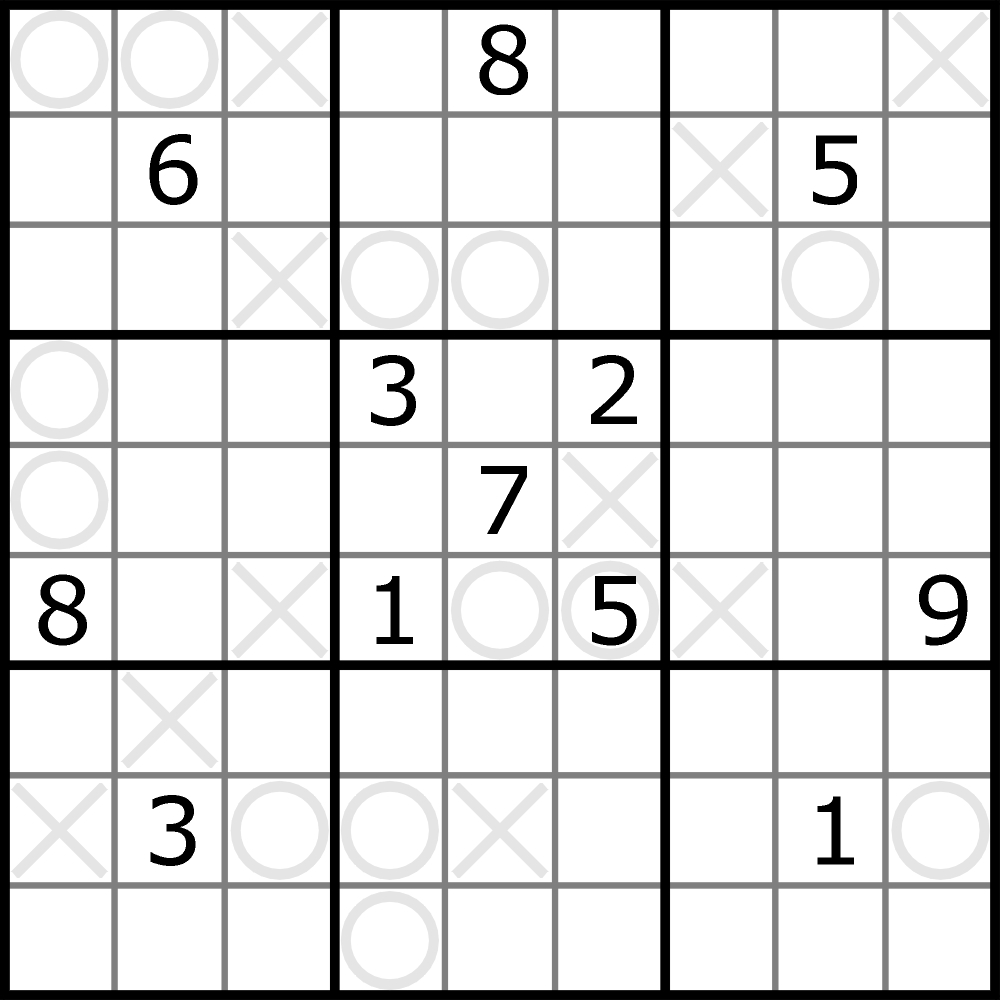
Po sąsiedzku

Krzyżyk jest w polu z cyfrą równą liczbie różnych cyfr znajdujących się w polach stykających się z polem z krzyżykiem  tylko rogiem.
Kółko jest w polu z cyfrą równą liczbie różnych cyfr znajdujących się we wszystkich polach stykających się z polem kółkiem.

Oczywiście w obu zadaniach obowiązują także zasady klasycznego sudoku.