Kwadratowy kwadrat
Klasyczna definicja kwadratu magicznego jest mniej więcej taka: kwadrat podzielony na n^2 jednakowych, kwadratowych kratek, w które wpisano liczby naturalne od 1 do n^2 tak, że ich sumy w rzędach, kolumnach i na przekątnych są jednakowe. Już jednak w XVI wieku definicję tę, gwoli wzbogacenia i uatrakcyjnienia zabawy, modyfikowano, udostępniając kratki dowolnym liczbom, a nie tylko kolejnym, pod warunkiem, że były one oczywiście różne i wyróżniały się jakąś szczególną własnością.
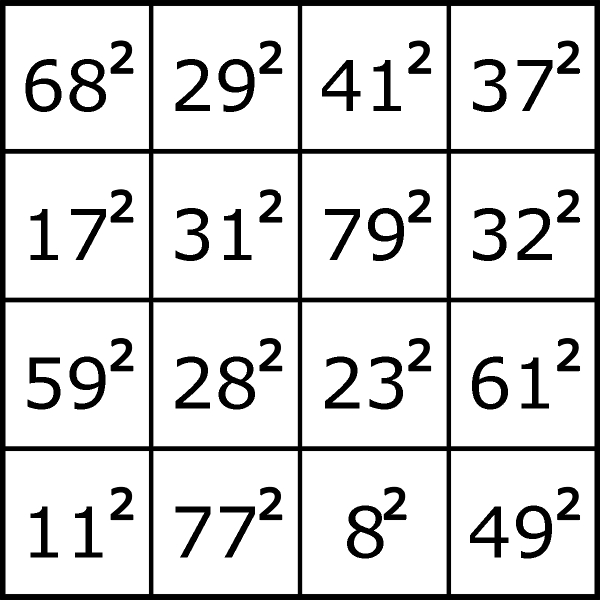
W roku 1770 Leonhard Euler (ten sam, któremu bywa przypisywane „odkrycie” sudoku) ułożył pierwszy kwadrat magiczny z kwadratami (drugimi potęgami), złożony z 16 kratek (4×4), z sumą magiczną 8515.
Euler lubił się chwalić takimi cudeńkami w listach do innych matematyków, dzięki czemu wiele z nich przetrwało – powyższy kwadrat zachował się w korespondencji do Lagrange’a. Warto zwrócić uwagę, że obfituje on w kwadraty liczb pierwszych. Prawdopodobnie ma to związek ze sposobem, jaki stosował Euler, aby stworzyć to kuriozum.
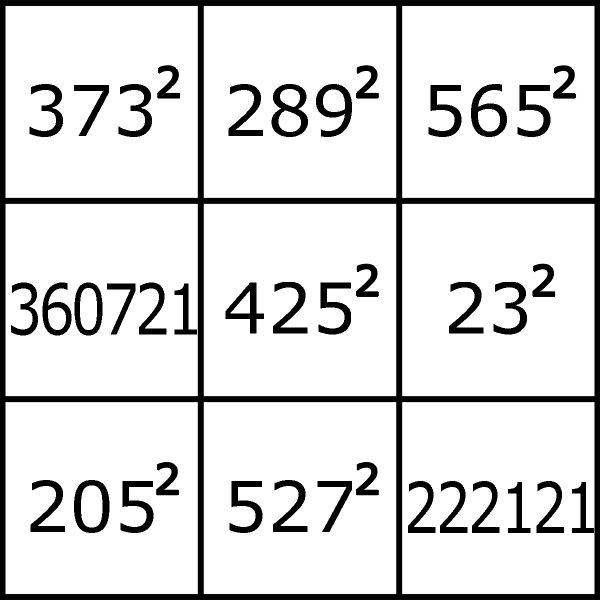
Natomiast próby ułożenia „kwadratowego” kwadratu magicznego 3×3 spełzły na niczym i „spełzają” do dziś. Ufundowana przed 12 laty przez Martina Gardnera nagroda (100 dolarów) dla tego, kto ułoży taki kwadrat albo udowodni, że jest to niemożliwe, pozostaje nietknięta wraz z rosnącym procentem. Trzy lata temu francuski matematyk Christian Boyer dorzucił 100 euro i butelkę szampana, na pozór łagodząc wymagania: wystarczy, aby kwadratami było tylko siedem liczb – jednak kwadrat powinien być całkiem inny niż poniższy (jak dotąd jedyny znany, w którym tylko dwie liczby nie są kwadratami ), czyli z dokładnością do różnych rodzajów przekształceń. Suma magiczna wynosi w tym przypadku 541875.
Jedno jest pewne: jeśli komuś uda się zainkasować 100 dolarów Gardnera za ułożenie kwadratu, a przy okazji 100 euro i szampana Boyera, to liczby w kratkach będą – w przeciwieństwie do nagród – gigantyczne.
Zanim staną Państwo w szranki, proponuję wprawkę, w której kwadrat 3×3 jest półmagiczny (bez magii na przekątnych) oraz kwadratowy, ale inaczej.
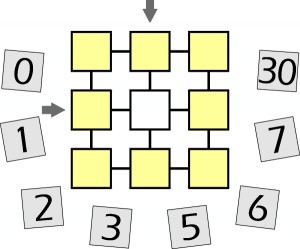
Osiem płytek z liczbami należy umieścić na żółtych polach tak, aby:
– sumy trzech liczb w każdym z czterech rzędów były różnymi kwadratami;
– po wpisaniu w środkowe pole odpowiedniej liczby (jakiej?), sumy liczb w dwóch rzędach wskazanych strzałkami także tworzyły kwadraty, ale kolejne (następujące bezpośrednio po sobie w ciągu kwadratów liczb całkowitych dodatnich).

Komentarze
sumy trzech liczb w każdym z czterech rzędów były różnymi kwadratami
Tu, jak rozumiem, jest błąd. Czy ja coś mylę ze względu na późną porę i krótki sen poprzedniej nocy?
Dobry żart.
Rozwiazanie:
5, 30, 1
9,132,3
2, 7, 0
Można obracać, byle nie 9 na 6.
Błędu, niestety, nie ma;).
mp
Pamiętam tego typu łamigłówkę (kwadrat półmagiczny) zamieszczoną na łamach „Wiedzy i Życia”. Wówczas rozwiązanie jej zajęło mi bardzo dużo czasu, a wynik przyszedł z nieoczekiwanej strony. Przez pomyłkę spojrzałem na rysunek odwrotnie niż zwykle i wówczas wszystko stało się jasne.
Pozdrawiam
Panie Marku! Znalazłem kwadrat magiczny 3×3 który zawiera 7 liczb będących kwadratami liczb naturalnych a pozostałe dwie liczby nie są, który różni się od podanego wyżej. Problem Christiana Boyera rozwiązany! To co, napijemy się tego szampana … ? Proszę o kontakt … 🙂
Szczerze mówiąc, nie chce mi się wierzyć. Podejrzewam żart lub jakieś qui pro quo. Ale dobry szampan nie jest zły, więc proszę o szczegóły na m.penszko@polityka.com.pl
m
Szczegóły przesłałem na Pana e-mail
Witam POMOCY
Jak podzielić kwadrat na 5 takich samych części?
4 razy ciach! – na 5 pasków równej szerokości.
mp