Kryptarytm Feynmana
Niejedno zadanie, zaliczane do matematyki rekreacyjnej, poszłoby w zapomnienie albo było znane tylko niewielu miłośnikom takich rozrywek, gdyby nie zainteresowała się nim jakaś wybitna osoba, a to zainteresowanie nie zostało ujawnione na szerszym forum. To trochę jak z wadowickimi (i nie tylko) kremówkami, które przeszły do historii dzięki wspominkom papieża.
Przed trzema laty w wydawnictwie Allen Lane ukazał się obszerny zbiór listów od i do Richarda Feynmana, wybranych i przygotowanych do druku przez jego przybraną córkę Michelle. Wybitny fizyk, noblista, jest szerzej znany także jako autor kilku poczytnych książek – zbiorów wspomnień, anegdot oraz zabawnych komentarzy i refleksji na tematy bliskie nie tylko naukowcom. O jednej z nich wspominałem w Łamiblogu, a Daniel Passent wspaniale ją zrecenzował i skomplementował w En passant. Z korespondencji uczonego również wyłania się obraz osoby niezwykłej, wyrazistej, ciekawej świata, nieco ekstrawaganckiej, o kontrowersyjnych poglądach i równie oryginalnym poczuciu humoru.
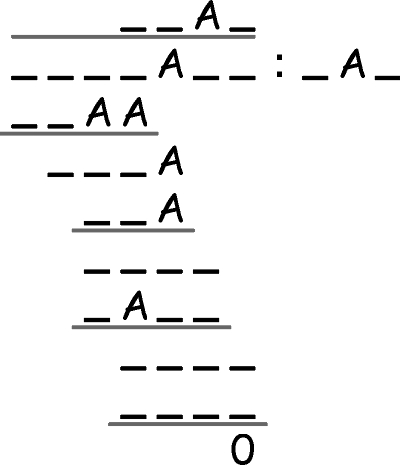
Jak większość umysłów ścisłych, Feynman miał smykałkę do łamigłówek. Wzmianki na ten temat pojawiają się zwłaszcza w listach z czasów studenckich. W jednym z nich, z listopada 1939 roku, adresowanym do matki, syn załącza łamigłówkę przeznaczoną dla ojca. Jest to rodzaj zadania zwany kryptarytmem, przykład wówczas bardzo trudny i pracochłonny (nie było kalkulatorów), a i dziś mogący sprawić sporo kłopotu. Oto jego polski zapis (oryginalny, amerykański na fotokopii listu).
Łatwo się domyślić, o co chodzi. Większość cyfr w zapisie dzielenia zastąpiono kreseczkami, a pozostałe literami A. Wszystkie litery skrywają taką samą cyfrę, która nigdzie nie jest zastąpiona kreską. Należy rozszyfrować kryptarytm. Czy komuś z Państwa starczy cierpliwości i czasu, aby się z tym uporać? A może ktoś poda w skrócie sposób rozwiązywania.
Feynman przyczynił się do rozpowszechnienia tej łamigłówki, ale nie jest ona jego dziełem. Została opublikowana w 1936 roku na łamach American Mathematical Monthly.


Komentarze
Sporo tego rodzaju lamiglowek zamiescil inz. Szczepan Jelenski w swoich dwoch slicznych ksiazkach popularyzujacych Matematyke – Lilavati i Sladami Pitagorasa.
Lilavati to była jedna z moich ulubionych książek z dzieciństwa. Połowę spisanych tam właściwości liczb znałem na pamięć, część została mi w głowie do dziś – a to już ponad dekada minęła 🙂
Po opisie łamigłówki spodziewałem się nie lada trudności w jej rozwiązaniu, albo, mając na uwadze postać autora, jakiegoś żartu.
Z moich podejrzeń wyszły nici. Zadanie okazało się łatwe i bezproblemowe. Wystarczyła kartka, ołówek, gumka do mazania i chwila wolnego czasu, aby uporać się z zadaniem.
Widać, że Feynman był bardzo łaskawy dla swojego ojca.
Sposób rozwiązania?
Można zauważyć w zapisie dzielenia miejsca ułatwiające znalezienie rozwiązania i na nich oprzeć poszukiwania cyfr.
Kluczowymi punktami są:
– pierwsza i trzecia pozycja w najwyższym rzędzie;
– trzy pozycje po znaku dzielenia;
– dwie litery „A” stojące obok siebie w poziomie;
– najniżej położona litera „A”.
3527876:484=7289
podstawą analizy było wyrażenie: * x *A* = **AA
sprowadzało się to do sprawdzenia kilkunastu przypadków,
cała sprawa kilkanascie minut, na spokojnie
Pozdrawiam P.
3527876:484=7289
Najpierw zauważamy,że A-A=0 i że I cyfra w 4-cyfr. odjemnej w II dzieleniu wynosi 1. Następnie ustalamy wartość A. W tym celu badamy iloczyny:
aAb
x c
——
deAA
oraz
aAc
x f
——
ghA
Ustalamy,że b=4, c=7,f=2(4×2=8 lub 4×7=28, ale 7 nie może być bo h nie może być 8)
h=6, a=4(z nast. cząstkowego mnożenia:8xa84=-872)
Ostatnia cyfra ilorazu to 9, bo w ostatnim cząstkowym dzieleniu cyfrą setek może być albo 2 albo 3 , a tylko 9×484=4356 spełnia ten warunek
Jedynie 8 może zastąpić A
może to oczywiste, ale dla mnie jakoś nie za bardzo… dlaczego I cyfra w 4-cyfr. odjemnej w II dzieleniu to 1?
ok, już sama do tego doszłam 🙂