Nielekko, niełatwo, przyjemnie
Główny organizator 17. Mistrzostw Świata, Vladimir Portugalov, specjalizuje się w układaniu zadań „perwersyjnych”. Rozwiązujący je zwykle wystawiają swoją cierpliwość na ciężką próbę, a umysł na przegrzanie. Nazywanie takich zadań łamigłówkami brzmi jakby eufemistycznie, bardziej pasowałoby określenie „łamiłby”. Przygotowując repertuar na Mistrzostwa Vladimir poskromił trochę swoją predylekcję do perwersji. Trochę, bo i tak na żadnych z szesnastu poprzednich mistrzostw poziom trudności nie był tak wysoki, jak tym razem. Wydaje się, że gdyby poprzeczka została podniesiona jeszcze nieco wyżej, to z przyjemności, jaką z definicji powinna być rozrywka umysłowa, niewiele by zostało – byłoby z pewnością umysłowo, ale jeśli rozrywkowo, to dla bardzo nielicznych.
Uczestnicy Mistrzostw wyrażali podobne opinie, a potwierdzeniem nadmiernej trudności zadań są rezultaty – w niektórych rundach najlepsi zgarniali ledwie połowę punktów możliwych do zdobycia. Nikt nie spodziewa się na mistrzostwach rozrywki lekkiej i łatwej, ale przyjemnej i owszem – jeśli nie dla wszystkich, to dla znacznej większości uczestników. Trudność zadań powinna więc być taka, aby nie pozbawiać satysfakcji tych, którym do szczytów daleko. Ciekawe, oryginalne łamigłówki, których w Mińsku nie brakowało, można smakować po zawodach, natomiast w trakcie dla każdego ważniejsze są maleńkie sukcesy. Wyznacznikiem umiejętności powinien być przede wszystkim czas rozwiązywania zadań – umiarkowanie trudnych, atrakcyjnych i różnorodnych; twarde i bardzo twarde orzechy mogą stanowić tylko przyprawę dla najtęższych głów. Warto pamiętać, że za szumną nazwą „Mistrzostwa Świata” kryje się nie tylko ostra walka kilku czy kilkunastu tytanów intelektu; zdecydowana większość startujących zjawia się także dlatego, że mają wielką ochotę, czas oraz po prostu ich na to stać – i to właśnie dzięki nim impeza ma sens i jaką taką rangę. Mam nadzieję, że organizatorzy kolejnych mistrzostw zadbają o to, aby zadowolenie z mini-sukcesów towarzyszyło jak największej liczbie uczestników. Za rok organizatorami będą Turcy, a w 2010 roku 19. Mistrzostwa Świata odbędą się w Polsce.
Z ochotą na mistrzostwa wiąże się niełatwa, przynajmniej dla mnie, zagadka: co skłania miłośników gimnastykowania szarych komórek do poświęcania czasu i inwestowania pokaźnej kwoty, by stawać w szranki? A w koszty trzeba jeszcze wliczyć zmęczenie i stres. Czyżby chęć sprawdzenia się, współzawodnictwa, przeżycia czegoś niezwykłego była wystarczająco silną motywacją? Być może w przypadku czołówki walka o prymat stanowi jakiś bodziec, choć ze zwycięstwem nie wiążą się żadne konkretne korzyści, a triumf i sława są niszowe. Podejrzewam, że to zagadka dla psychologów. Dla miłośników główkowania mam inną propozycję: kolejne zadanie z Mińska – oryginalne, a czy „perwersyjne” – proszę ocenić samemu.
Kółka na strzałkach
Do kółek należy wpisać liczby od 1 do 13 – każdą raz. Sumy liczb na strzałkach wskazujących na każdy czerwony punkt i na strzałkach wychodzących z tego samego punktu powinny być równe.
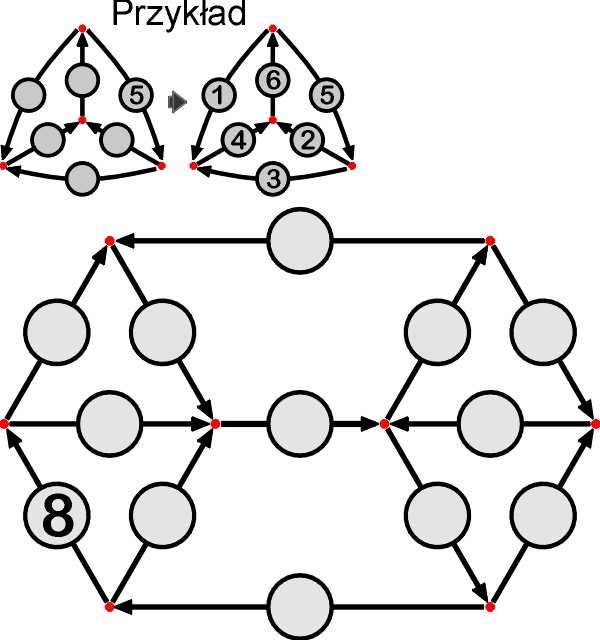

Komentarze
Nie podoba mi się nazwa tego zadania. „Numery na strzałkach” to wprawdzie tytuł zgodny z tym, co widać na obrazku, ale ja bym nazwał to zadanie ambitniej, np. „Graf przepływów”. Choć pewnie jeszcze lepsze byłoby dowolne słowo w języku japońskim
No, pięknie! Do tytułu istotnie, ani autor ani tłumacz:) się nie przyłożyli.
m
Trudno narysowac wynik, ale bedzie to wygladalo mniej wiecej tak:
3
2 5 10 7
6 12 11
8 1 13 4
9
Rozwiązanie podane „wierszami”: 3, 2-5-10-7, 6-12-11, 8-1-13-4, 9.
Pozdrawiam
Rozwiązanie dzisiejszej miażdżygłówki jest następujące:
Rzędami: 3, 2, 5, 10, 7, 6, 12, 11, (8), 1, 13, 4, 9.
Było miło!
No tak… a jak mówiłem podczas jednej z rund drużynowych o tym, że graf zależności jest dwudzielny i o rozbijaniu permutacji na cykle, to patrzyli na mnie jak na idiotę… 🙂
Jeśli chodzi o trudność, to trochę się nie zgodzę. Na mistrzostwach nie było żadnych wyjątkowo trudnych zadań (no, może poza gigantami, ale to wynikało z czasochłonności i stopnia ryzyka, biorąc pod uwagę wagę każdego zadania). Dodatkowo większość zadań „kombinacyjnych” miała element, który bardzo zawężał obszar przeszukiwań.
Pomijając wpadkę z ostatnią rundą, stwierdziłbym że praktycznie wszystkie zadania były ciekawe i warte swojego zaistnienia na mistrzostwach. Zgodzę się, że brakowało zadań o bardzo niskim stopniu trudności, ale ja nie widzę dla nich sensu na takich mistrzostwach.
Podaję rzędami:
3
2,5,10,7
6,12,11
8,1,13,4
9
Jesli to zadanie jest typowe dla mistrzostw, to ja dziekuje.
Przeciez to jest zniechecajace probowanie i bladzenie albo jak kto woli rozwiazywanie ukladu rownan diofantycznych.
a
Rozwiązanie zadania nie sprawia aż tak wiele kłopotów jak pisze Andy.
Faktycznie trzeba pokombinować i zrobić kilka prób. Ale ujawniona liczba
oraz zachodzące relacje mniejszości (większości) znakomicie to zadanie ułatwiają. W warunkach turniejowych mogło jednak sprawić duże trudności.
Rzędami od góry
3
2 5 10 7
6 12 11
8 1 13 4
9
Pozdrowienia i jeżeli można, to proszę o częstsze wpisy (dla podtrzymania kondycji).
Antyp
od góry i lewej:
3
2 5 10 7
6 12 11
8 1 13 4
9
Nie podzielam opinii jakoby zadanie było bardzo trudne (choć może akurat miałem szczęście). Bywały na łamiblogu takie, co sprawiały mi większą trudność, a to było całkiem przyjemne.
Podaję rozwiązanie rządkami:
– 3
– 2, 5, 10, 7
– 6, 12, 11
– 8, 1, 13, 4
– 9
Zacząłem od określenia wszystkich pól, na których mogła znajdować się liczba 13 – są to pola przy węźle środkowym po prawej stronie. Wydało mi się więc, że do węzła musi ‚wpływać’ (i ‚wypływać’) jakaś duża liczba. Założyłem sobie, że to 23, a potem już kombinowałem, dobierałem i wyszło to co wyżej.
Zadanie makabryczne, wysysajace resztki checi do logicznego rozumowania.
3
2 5 10 7
6 12 11
8 1 13 4
9
Po znalezieniu rozwiązania, nie satysfakcjonującą mnie metodą, postanowiłem nie odpowiadać na to zadanie. Jednak, po przeczytaniu komentarza Andy zdecydowałem się zadać pytanie lepiej poinformowanym. Jaką to metodą rozwiązuje się tego typu zadania? Bo jeśli metoda polega na przeszukiwaniu drzewa rozwiązań (nawet przy kilku raczej oczywistych spostrzeżeniach), to wybaczcie, ale ja również nie znajduję uzasadnienia umieszczenia takiego zadania na mistrzostwach świata. Czy od uczestników mistrzostw tej rangi oczekuje się jedynie szybkiego uzyskiwania rozwiązań, czy też dobór zadań powinien uwzględniać konieczność poszukiwania bardziej wyrafinowanych metod?
Z pozdrowieniami,
Jazz_off
Właśnie to było takim, w miarę typowym, zadaniem kombinacyjnym – sprawdzenia wszystkich kombinacji mija się z celem. Ale po zauważeniu pary małych rzeczy zadanie staje się bardzo proste.
Mi się takie zadania podobają, bo liczą się tutaj tak na prawdę 3 umiejętności:
– zauważanie nietypowych relacji (tego w sudoku raczej nie doświadczymy)
– oszacowanie czy znalezniony „zestaw spostrzeżeń” wystarcza, żeby uwinąć się z zadaniem w rozsądnym czasie
– no i nieszczęsne szybkie analizowanie możliwych rozwiązań
Co do tych spostrzeżeń jeśli chodzi o to zadanie:
„poetykietujmy” liczby na diagramie
A
BCDE
EFG
HIJK
L
H jest równe 8.
F równe H + A
F, J, L to są duże liczby, a A, I i K są małe (A <= 5, I, K 2 lub 3, H->2+6 lub 3+5
2) A=5 -> I+K = 1+3 -> H=2+6
Przy każdej z nich trzeba potem tylko sprawdzić czy „wychodzi” prawy górny trójkąt.
Po znalezieniu tych możliwości zadanie idzie w jakąś minutę, więc jednak głównym problemem zostaje spotrzegawczość, a nie analizowanie drzew.
Inna sprawa jest taka, że na mistrzostwach przewidywany czas na to zadanie to trochę ponad 3 minuty 🙂
Z Polaków, podczas zawodów, to chyba jedynie „nasz Jan” to zadanie zrobił.
Uważam, że tego typu zadań nie powinno być na mistrzostwach. Chodzi mi o zadania, w których trzeba cos zakładać i sprawdzać, czy dalej się zgadza. W takich zadaniach zbyt dużą rolę odgrywa szczęście. Jak ktoś zgadnie jedną czy kilka początkowych liczb, to błyskawicznie może rozwiązać zadanie. Jak ktos nie zgadnie, dochodzi po pewnym czasie do sprzeczności, musi się cofać, wycierać gumką wpisane liczby i traci mnóstwo czasu. Jak dla mnie – traci niesprawiedliwie.
Pawiem szczerze, że nie zostałem przekonany, tym bardziej, że Psyho popełnił kilka oczywistych błędów.
Oznaczmy porządniej poszczególne strzałki:
A
BCDE
FGH
IJKL
M
To co nie budzi żadnych wątpliwości, to równania wynikające z I prawa Kirchoffa, czyli suma prądów wpływających do węzła jest równa sumie prądów wypływających. Dodatkowo, kombinacje tych równań pozwalają zauważyć, że:
1) A+M=G.
2) A, J, L oraz B albo F, to liczby od 1 do 4. Zatem pozostałe litery mają wartości >4
3) 9<=M<=12.
4) 11<=G<=13. Podobnie dla K.
5) 5<=E<=12.
6) 6<=D<=13. Podobnie dla H.
Niestety cała reszta, to jak ja to nazywam – łażenie po drzewie, czyli poszukiwanie różnowartościowego przyporządkowania literom wartości, jednocześnie spełniających powyższe założenia. Niby nic, a jednak właśnie to budzi u mnie najwięcej zastrzeżeń.
Pozdrawiam,
Jazz_off
No chyba nie tak oczywistach, skoro nie zauważyłem tych błędów (pomijając felerne poetykietowanie) 🙂
W każdym razie, czy chcecie czy nie, ogrom zadań się do tego sprowadza – zwłaszcza że często w trudniejszych „logicznych” zadaniach bardziej się opłaca strzelić, niż logicznie analizować. Oczywiście, mówię tutaj z perspektywy zawodów.
Co do tego szczęścia, to jest to nietrafione, bo:
– jest wiele takich zadań, więc po kilku i tak się „wyrówna”, a ci, którzy strzelali, zamiast myśleć padną już przy drugim.
– to samo szczęście występuje nawet jak rozwiązujesz sudoku. Często w trudniejszych diagramach cały diagram „się blokuje” dopóki nie znajdzie się singla (czyli miejsca gdzie możesz wpisać tylko jedną cyfrę) – znalezienie tego, to też w pewnym sensie jest szczęście.
– tego typu zadania są tworzone kiedy drzewo przeszukiwań (liczba potencjalnych rozwiązań) jest małe, w przeciwnym wypadku rzeczywiście takie zadanie jest nieporozumieniem.
Podczas rozwiązywania zadań odrobina szczęścia zawsze się przydaje, ale ważniejsze są umiejętności, które wymienił Psyho.
Nie wiem jakie zadania (oprócz zamieszczonych na Łamiblogu) były na mistrzostwach, ale patrząc na tabelę wyników, wątpię, aby zadania były przeznaczone dla szczęściarzy. Gdyby tak było, to w czołówce nie byłoby tych samych nazwisk co zwykle.
Pozdrawiam
PS Szczęście, to trzeba mieć w lotto.
Moim zdaniem zadania, w którym bardziej opłaca się strzelać niż analizować, nie można uważać w pełni za „logiczne”. Dla mnie zadanie logiczne to takie, w którym stopniowo udaje się JEDNOZNACZNIE znajdować poszczególne elementy rozwiązania (np. wpisywac do diagramu kolejne cyfry) albo przynajmniej stopniowo tak ograniczać zakresy wartości, przyjmowanych przez pewne elementy, żeby pozwalało to efektywnie ograniczać zakresy wartości innych elementów i w ten sposób jednoznacznie zmierzać do końcowego rozwiązania. Oczywiście dopuszczalne jest przyjmowanie założeń na jeden czy kilka kroków, ale tak, by nie trzeba było posługiwac się gumką.