Nie ma lekko
Już przynajmniej dwukrotnie zapraszałem Państwa do zabawy indukcyjnej polegającej na rozszyfrowywaniu zasad łamigłówki wyłącznie na podstawie przykładu z rozwiązaniem. Propozycje były połączeniem przyjemnego z pożytecznym także w tym sensie, że zaproszenie stanowiło równocześnie prośbę o pomoc. Łamigłówki pochodziły z japońskiego pisma, a z tłumaczeniem opisu miałem problem, no i jako „induktor” spisywałem się miernie. Z czasem doszedłem do wniosku, iż taka zabawa jest na tyle oryginalna, że może być sfingowana, czyli nie muszę czekać, aż problem pojawi się w rzeczywistości.
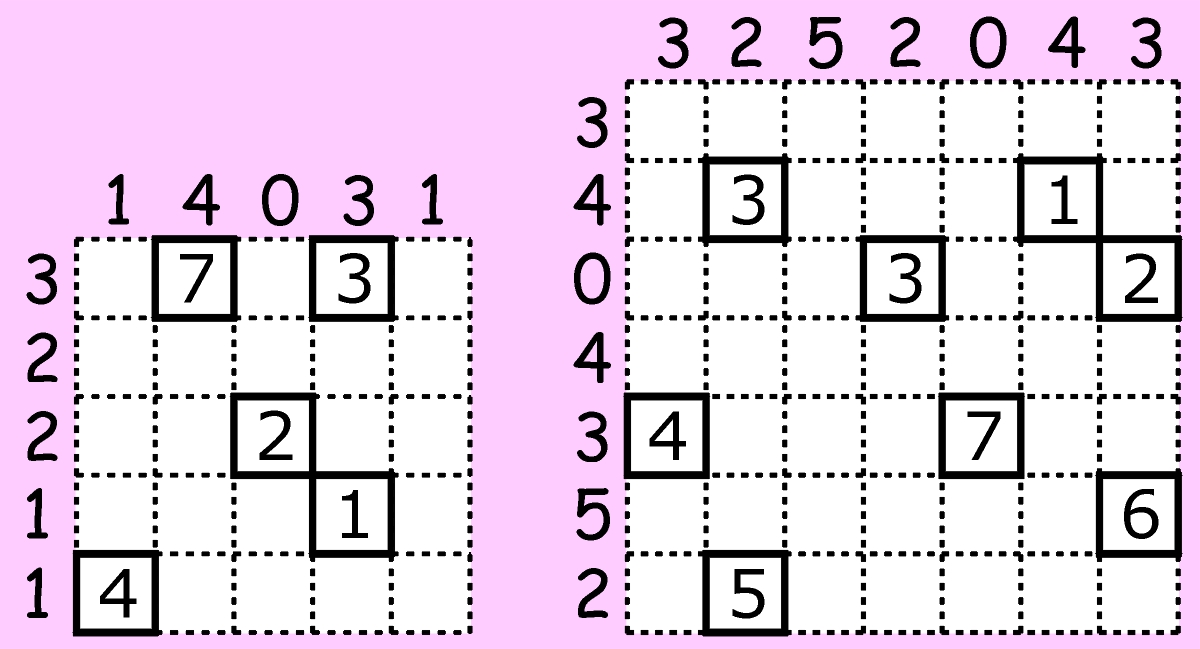
Rysunek zamieszczony poniżej przedstawia przykład z rozwiązaniem łamigłówki (i jego zapisem), której zasady znam, ale nie podam. Nie ma lekko. Sam musiałem się nieźle nagłowić, żeby je rozgryźć (to także dziełko z kraju sake i sushi), więc nie będę pozbawiał Państwa tej przyjemności.
Dla okazjonalnych rozwiązywaczy zadanie może okazać się całkiem twardym orzechem, ale dla stałych bywalców Łamiblogu to raczej pestka. A kto ją rozłupie, na tego czeka nagroda, a nawet dwie – poniższe zadania do rozwiązania zgodnie z rozszyfrowanymi na podstawie przykładu regułami. Pierwsze jest bardzo łatwe, drugie znacznie trudniejsze.

Komentarze
c7c3c
cc-bc
bc2bb
-cb1b
4c-bc
bccbbbb
b3-bb1b
—3cb2
-bcbbbb
4ccc7bc
-ccccc6
b5cbcbb
bardzo sympatyczne zadanko !!
Pozdrawiam PM.
Rozwiązanie 1 zadania
c7c3cccbb-bc2bb-c-1-4c-bc
zasady
1)każda liczba wewnątrz diagramu wskazuje sumę ilości czarnych kółek w kolumnie i wierszu, w których ta liczba jest położona
2) liczby na zewnątrz są różnicą ilości białych i czarnych kółek odpowiednio w wierszu lub kolumnie (różnica jest wartością absolutną tych dwóch ilości)
Antyp
Zadania bardzo ciekawe, chociaz niezbyt trudne.
zadanie latwiejsze (z lewej):
c7c3c
cc-bc
bc2bb
-cb1b
4c-bc
zadanie trudniejsze (z prawej)
bccbbbb
b3-bb1b
—3cb2
-bcbbbb
4ccc7bc
-ccccc6
b5cbcbb
Orzeszek:
c 7 c 3 c
c c – b c
b c 2 b b
– c b 1 b
4 c – b c
Orzech:
b c c b b b b
b 3 – b b 1 b
– – – 3 c b 2
– b c b b b b
4 c c c 7 b c
– c c c c c 6
b 5 c b c b b
Potencjalne zasady łamigłówki ująłbym w dwóch zdaniach:
1. Liczba przy wierszu/kolumnie to moduł różnicy liczb białych i czarnych kółek w danym wierszu/kolumnie.
2. Liczba wewnątrz diagramu to suma czarnych kółek w wierszu i kolumnie, na skrzyżowaniu których się ta liczba znajduje.
Bardzo sympatyczna łamigłówka 🙂 .
Dwie zasady:
Cyfry w polach oznaczają sumę czarnych kamieni w kolumnie i wierszu przechodzących przez to pole.
Cyfry na brzegu diagramu oznaczają różnicę bezwzględną/dodatnią pomiędzy sumą kamieni czarnych, a sumą kamieni białych odpowiednich wierszy / kolumn.
zad.1
c7c3c
cc-bb
bc2bb
-cb1b
4c-bc
zad.2
bccbbbb
b3-bb1b
—3cb2
-bcbbbb
4ccc7bc
-ccccc6
b5cbcbb
1. w niektóre pola wpisać kółka
2. kółka są białe lub czarne
3. liczby po bokach oznaczają różnicę w ilości białych i czarnych kółek w danym rzędzie bądź kolumnie
4. liczba w środku diagramu oznacza łączną liczbę czarnych kółek w rzędzie i kolumnie, na których skrzyżowaniu się znajduje
c7c3c
cc_bc
bc2bb
_cb1b
4c_bc
bccbbbb
b3_bb1b
___3cb2
_bcbbbb
4ccc7bc
_ccccc6
b5cbcbb
pozdro
odpowiedź:
1.
c7c3c
cc-bc
bc2bb
-cb1b
4c-bc
2.
bccbbbb
b3-bb1b
—3cb2
-bcbbbb
4ccc7bc
-ccccc6
b5cbcbb
😀
Na wszelki wypadek przypominam: komentarze z rozwiązaniami (poprawnymi) uwalniam dzień przed następnym wpisem.
mp
Białe i czarne kółka można umieścić w diagramie według następujących reguł:
– cyfry wewnątrz diagramu, to ilość czarnych kółek w pionie i poziomie względem danej cyfry;
– cyfry na zewnątrz diagramu, to w danym wierszu lub kolumnie wartość bezwzględna różnicy między liczbą białych i czarnych kółek.
Mała pestka:
c7c3c
cc-bc
bc2bb
-cb1b
4c-bc
Duża pestka:
bccbbbb
b3-bb1b
—3cb2
-bcbbbb
4ccc7bc
-ccccc6
b5cbcbb
Pozdrawiam
Liczby po bokach diagramu oznaczaja roznice ilosci czarnych i bialych krazkow w danym wierszu/kolumnie; liczby wewnatrz diagramu oznaczaja ilosc czarnych krazkow lacznie w danym wierszu i kolumnie.
(nie wiem czy to dobre zasady, ale daje sie wedlug nich rozwiazac…)
c7c3c
cc-bc
bc2bb
-cb1b
4c-bc
bccbbbb
b3-bb1b
—3cb2
-bcbbbb
4ccc7bc
-ccccc6
b5cbcbb
Trudniej poszło mi z pierwszym , małym zadaniem – myślałem , że doszedłem do sprzeczności , gdy tymczasem należy przyjąć regułę , że nie wszystkie czarne piony są ujawnione liczbami .
c7c3c
cc-bc
bc2bb
-cb1b
4c-bc
Mając komplet reguł (liczby w diagramie pokazują ilość czarnych pionów w danym wierszu i kolumnie , a liczby poza diagramem pokazują różnice w ilości białych i czarnych pionów w danym wierszu albo kolumnie) drugie zadanie rozwiązuje się niezbyt trudno .
bccbbbb
b3-bb1b
– – -3cb2
-bcbbbb
4ccc7bc
-ccccc6
b5cbcbb
Dziękuję , pozdrawiam i proszę o więcej .
AC
Zasady:
Diagram należy uzupełnić czarnymi i białymi kółkami tak, aby spełnione były poniższe warunki:
– każda cyfra wewnątrz diagramu oznacza liczbę czarnych kółek w wierszu
i kolumnie, na przecięciu których znajduje się dana cyfra,
– każda cyfra na zewnątrz diagramu oznacza bezwzględną różnicę liczby
czarnych i białych kółek w odpowiednim wierszu/kolumnie.
Zadanie 1:
c7c3c
cc?bc
bc2bb
?cb1b
4c?bc
Zadanie 2:
bccbbbb
c3?bb1b
???3cb2
?bcbbbb
4ccc7bc
?ccccc6
b5cbcbb
Pozdrawiam
Łatwiejsze:
c7c3c
cc-bc
bc2bb
-cb1b
4c-bc
Trudniejsze, ale nie bardzo trudne na szczęście:
bccbbbb
b3-bb1b
—3cb2
-bcbbbb
4ccc7bc
-ccccc6
b5cbcbb
Ogólnie całkiem sympatyczne zadanie.
Zasady zabawy:
– liczba w diagramie oznacza, ile jest czarnych kółek w rzędach, na przecięciu których ta liczba się znajduje
– liczba przed (nad) rzędem oznacza bezwzględną różnicę między liczbami czarnych i białych kółek w danym rzędzie
Rozwiązania:
łatwe: c7c3c/cc-bc/bc2bb/-cb1b/4c-bc
trudne: bccbbbb/b3-bb1b/—3cb2/-bcbbbb/4ccc7bc/-ccccc6/b5cbcbb
Rozwiązuje się bardzo przyjemnie.
Pozdrawiam i proszę o więcej takich indukcyjnych zabaw.
and
Witam.
Rozwiązania:
łatwe:
c7c3c
cc-bc
bc2bb
-cb1b
4c-bc
trudne(?):
bccbbbb
b3-bb1b
—3cb2
-bcbbbb
4ccc7bc
-ccccc6
b5cbcbb
zasady:
Każda liczba wewnątrz diagramu wskazuje ile jest czarnych kul w kolumnie i wierszu w którym znajduje się dana liczba. Liczby na zewnątrz diagramu podają bezwzględną różnicę liczby kul czarnych i białych w danym wierszu/kolumnie.
Pozdrawiam
Regułę nie jest trudno wyłapać: cyfry przy brzegach oznaczają różnicę między liczbą czarnych i białych kulek w poszczególnych kolumnach lub rzędach. Natomiast cyfry w polach obwiedzionych ramką wskazują ile w sumie czarnych kulek występują w rzędzie i kolumnie, w których jest ta cyfra.
Pierwsze zadanie nawet nie tyle co proste, a szkoleniowe, wręcz trywialne. Drugie na pewno trudniejsze, ale bez przesady. Wystarczyło kilka minut, żeby na spokojnie zrobić.
Rozw1:
?7 ?3 ?
??- ??
??2 ??
-?? 1?
4? – ??
Rozw2:
???????
? 3 – ?? 1?
– – – 3 ??2
– ??????
4??? 7??
– ?????6
? 5?????
pzdr
eh, niestety nie dało rady wpisać znaków sposobem alt+liczba,
to jeszcze raz rozwiązania:
1:
C7C3C
CC-BC
BC2BB
-CB1B
4C-BC
2:
BCCBBBB
B3 – BB1B
– – – 3CB2
– BCBBBB
4CCC7BC
-CCCCC6
B5CBCBB
1)
c7c3c
ccxbc
bc2bb
xcb1b
4cxbc
2)
bccbbbb
b3xbb1b
xxx3cb2
xbcbbbb
4ccc7bc
xccccc6
b5cbcbb
Zasady:
-liczba w kwadraciku we wnętrzu tabeli mówi ile jest czarnych kółek w rzędzie plus w kolumnie wyznaczonych przez ten kwadracik
-liczba na brzegu na zewnątrz tabeli mówi, ile wynosi suma kółek w danym rzędzie lub kolumnie ( b+c to zero)
Reguły zadania można podać w jednym zdaniu (choć długim):
Uzupełnij przedstawiony diagram umieszczając odpowiednią liczbę czarnych i białych znaczników tak, aby liczba czarnych znaczników w pionowej kolumnie i poziomym rzędzie, na których przecięciu znajduje się cyfra w kratce była zgodna z tą cyfrą, natomiast cyfra nad kolumną lub obok rzędu była zgodna z bezwględną różnicą liczby czarnych i białych znaczników w tej kolumnie lub tym rzędzie.
I zgodnie z tymi regułami rozwiązanie zadań będzie nastepujące:
c7c3c
cc-bc
bc2bb
-cb1b
4c-bc
bccbbbb
b3-bb1b
—3cb2
-bcbbbb
4ccc7bc
-ccccc6
b5cbcbb
c7c3c
cc-bc
bc2bb
-cb1b
4c-bc
bccbbbb
b3-bb1b
—3cb2
-bcbbbb
4ccc7bc
-ccccc6
b5cbcbb
To zadanie troche przypomina „latarniowce”