1 = 2
Wydaje się, że lista sofizmatów matematycznych, a ściślej reguł, które są w nich łamane, jest krótka i zamknięta. W gruncie rzeczy temat został merytorycznie wyczerpany w książce niemieckiego matematyka Waltera Lietzmana Wo steckt der Fehler? (Gdzie tkwi błąd?, PZWS 1958), której pierwsze wydanie ukazało się w roku 1913. Pojawiają się natomiast pomysły dość niezwykłe formalnie. Otrzymałem niedawno od znajomego przykład, który wydał mi się oryginalny i zabawny.
Oto dowód, że 1 = 2.
Zaczynamy od równości:
Jedynkę w mianowniku zastępujemy wyrażeniem
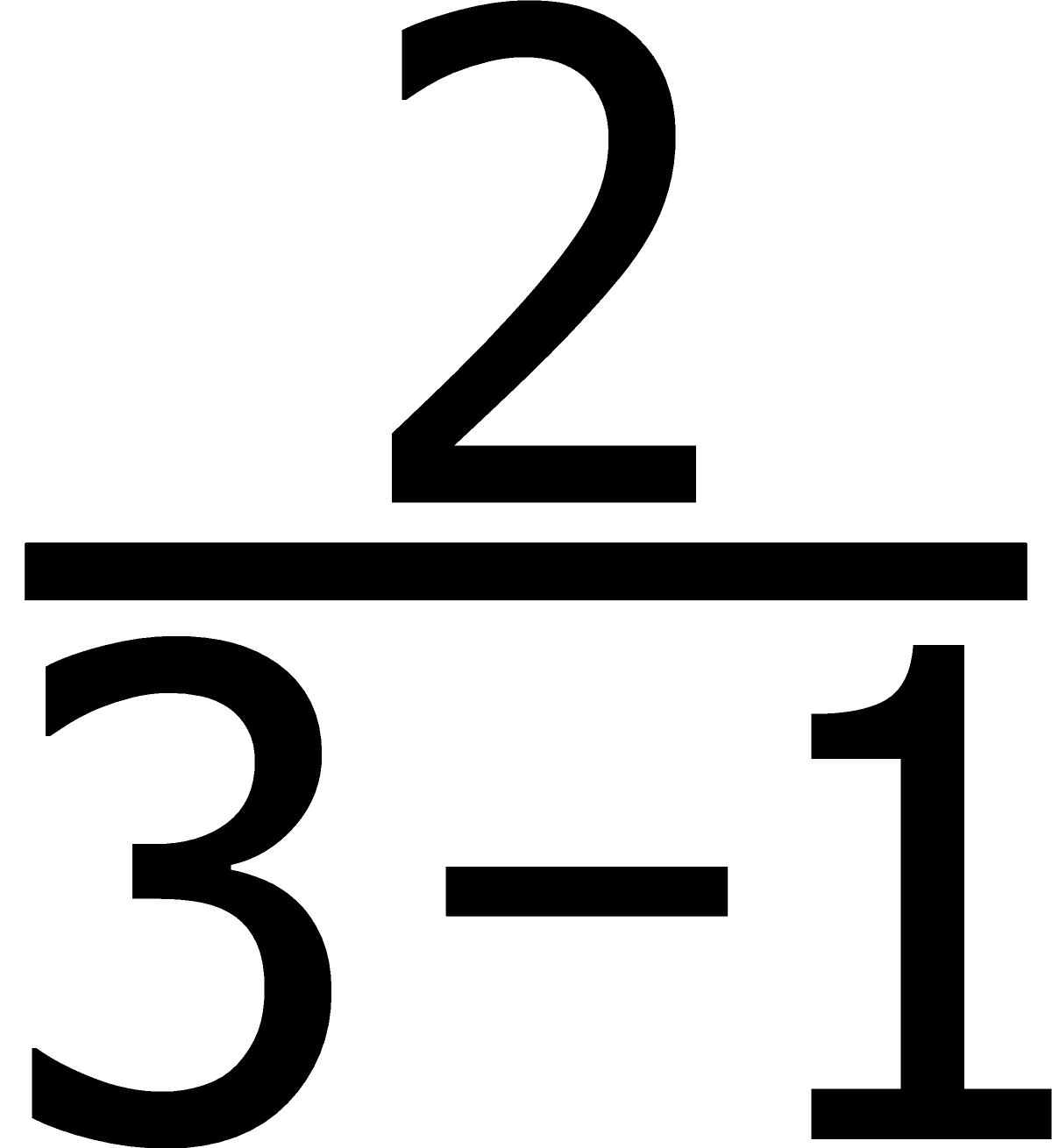
w wyniku czego otrzymujemy równość
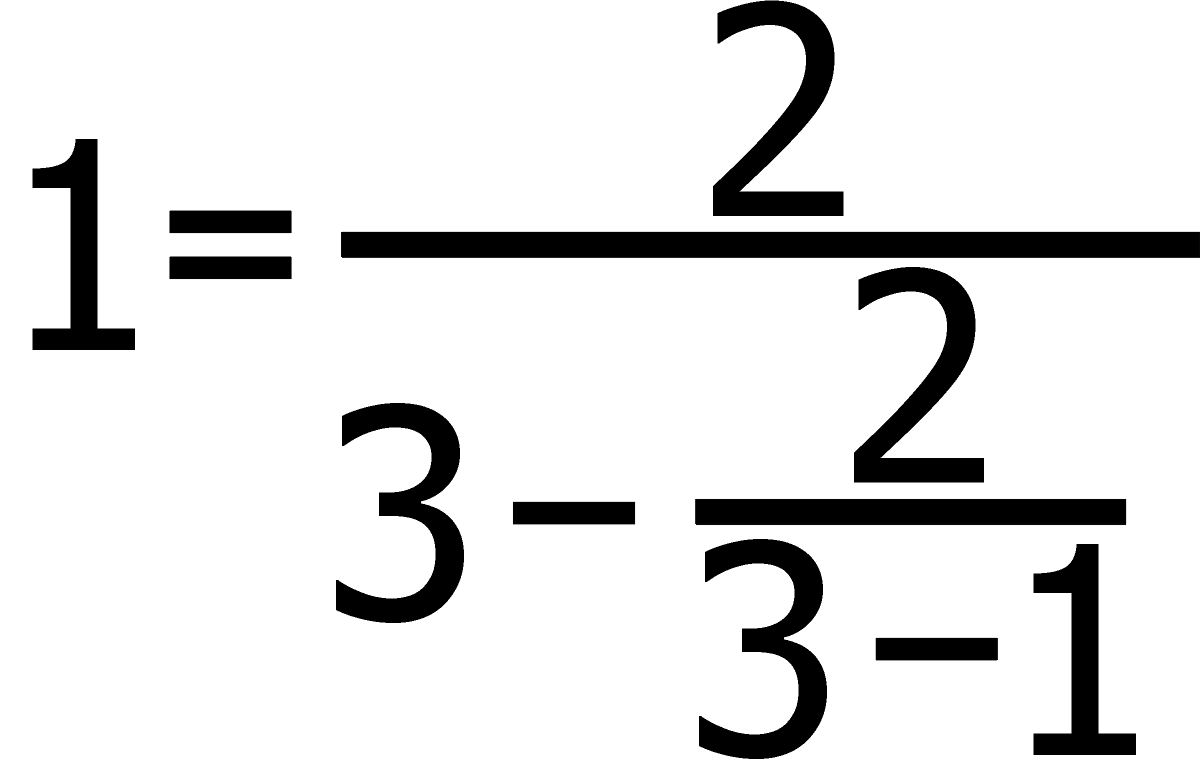
Powtarzamy to podstawienie jeszcze raz, czyli powstaje
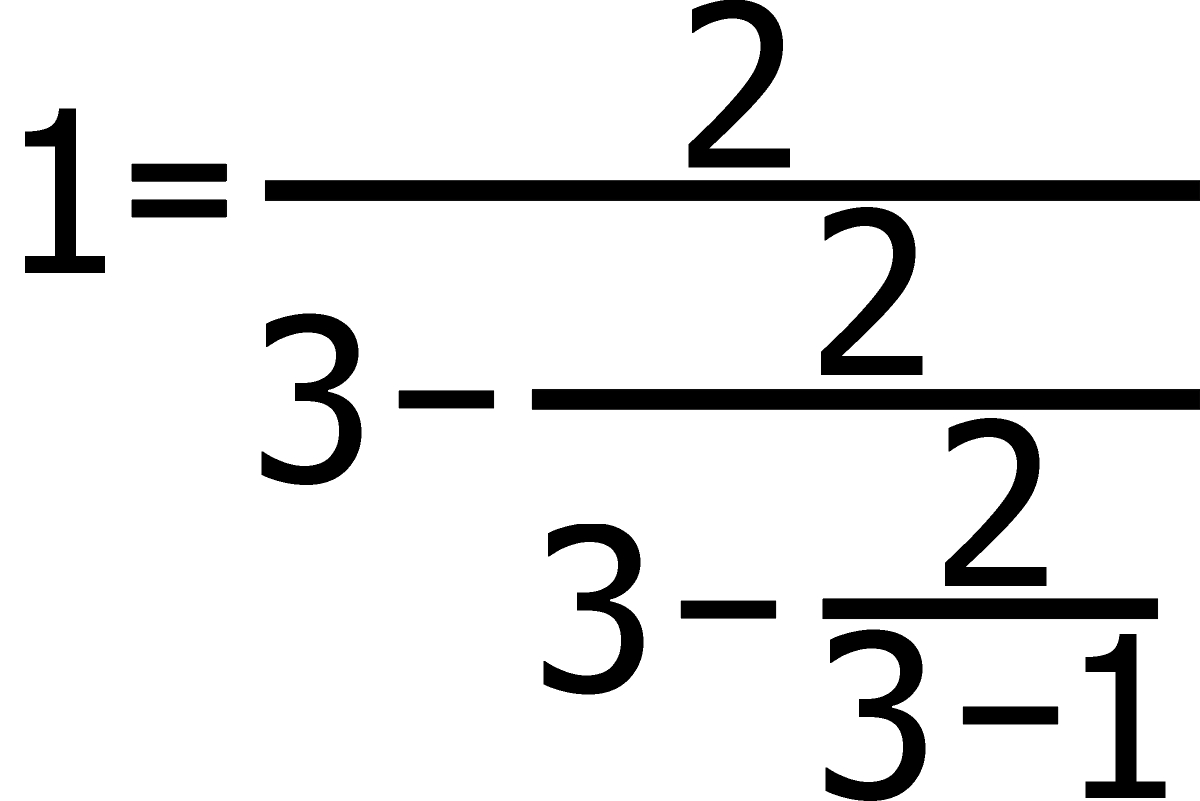
Kontynuujemy taką podmiankę w nieskończoność, a zatem
Na razie przerywamy ten wątek i zaczynamy nowy od równości
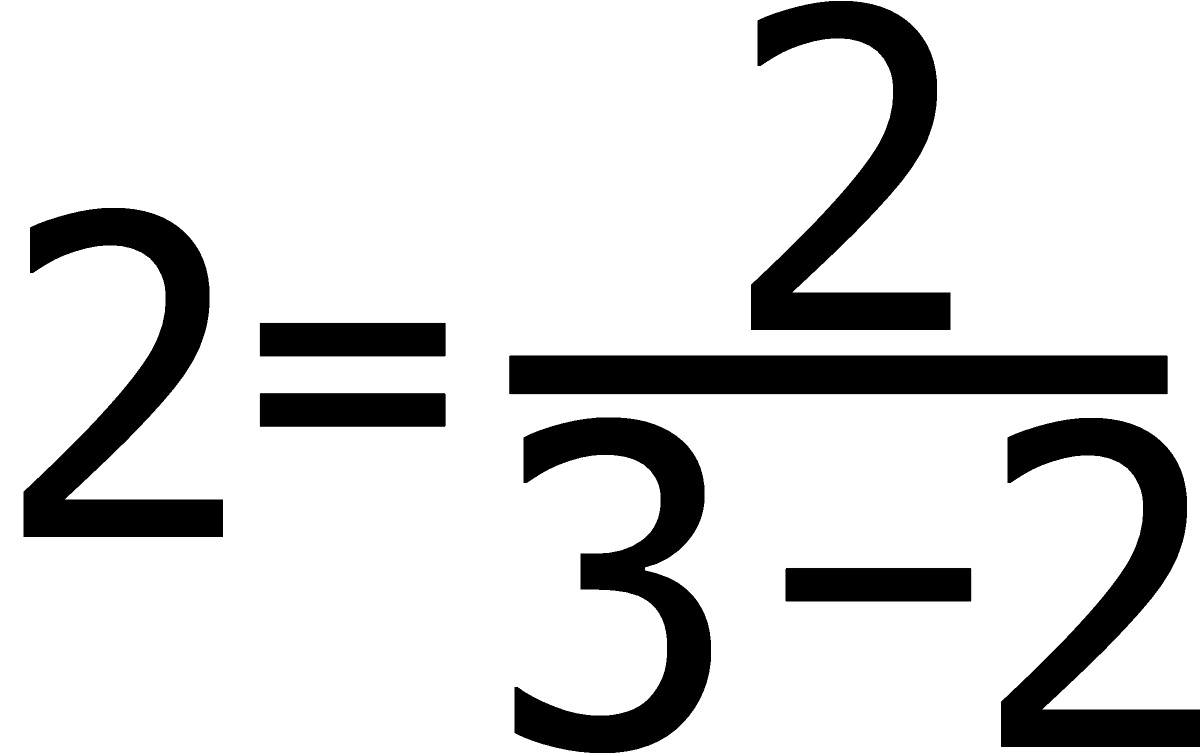
Dwójkę w mianowniku zastępujemy wyrażeniem
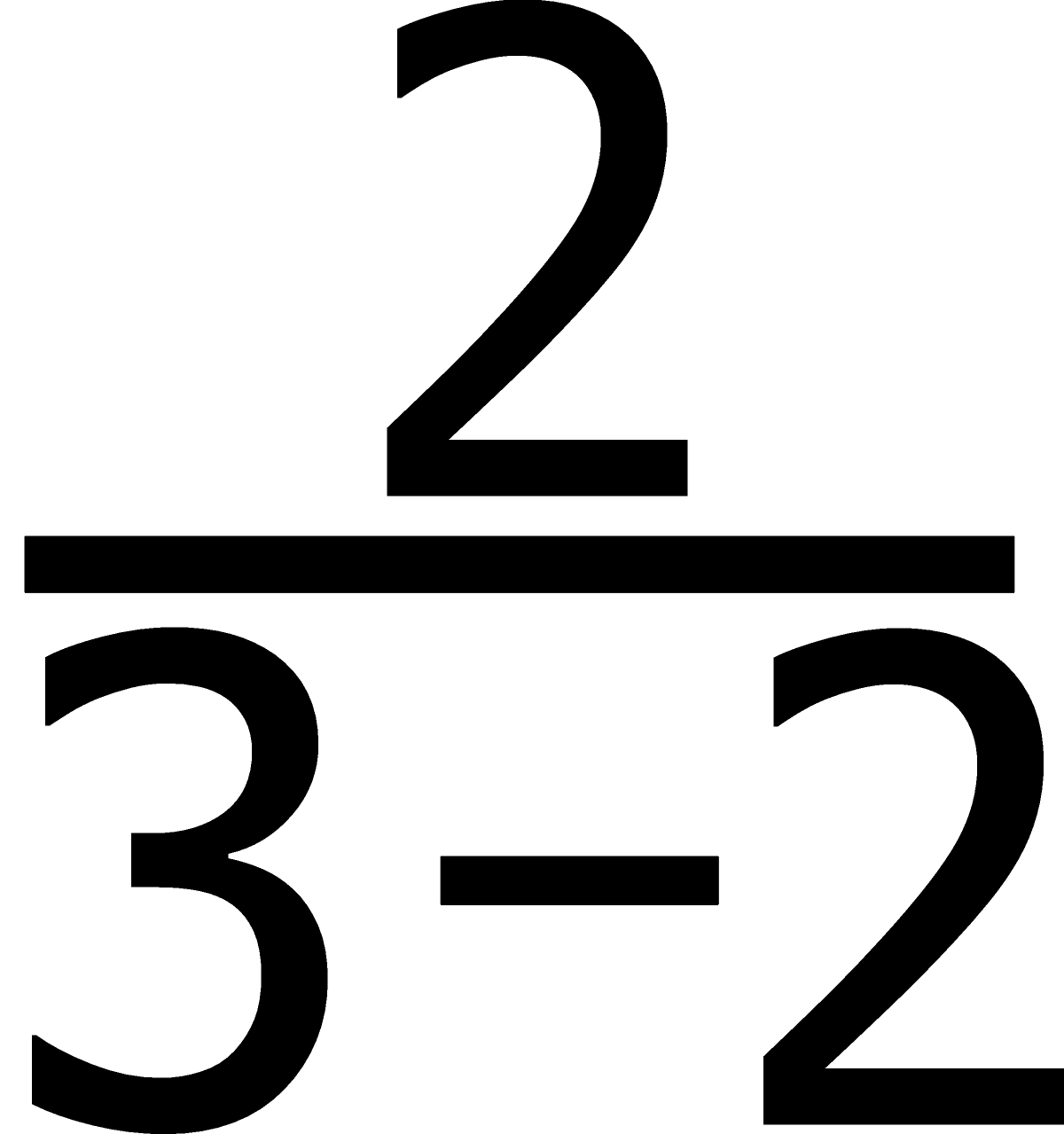
tworząc równość
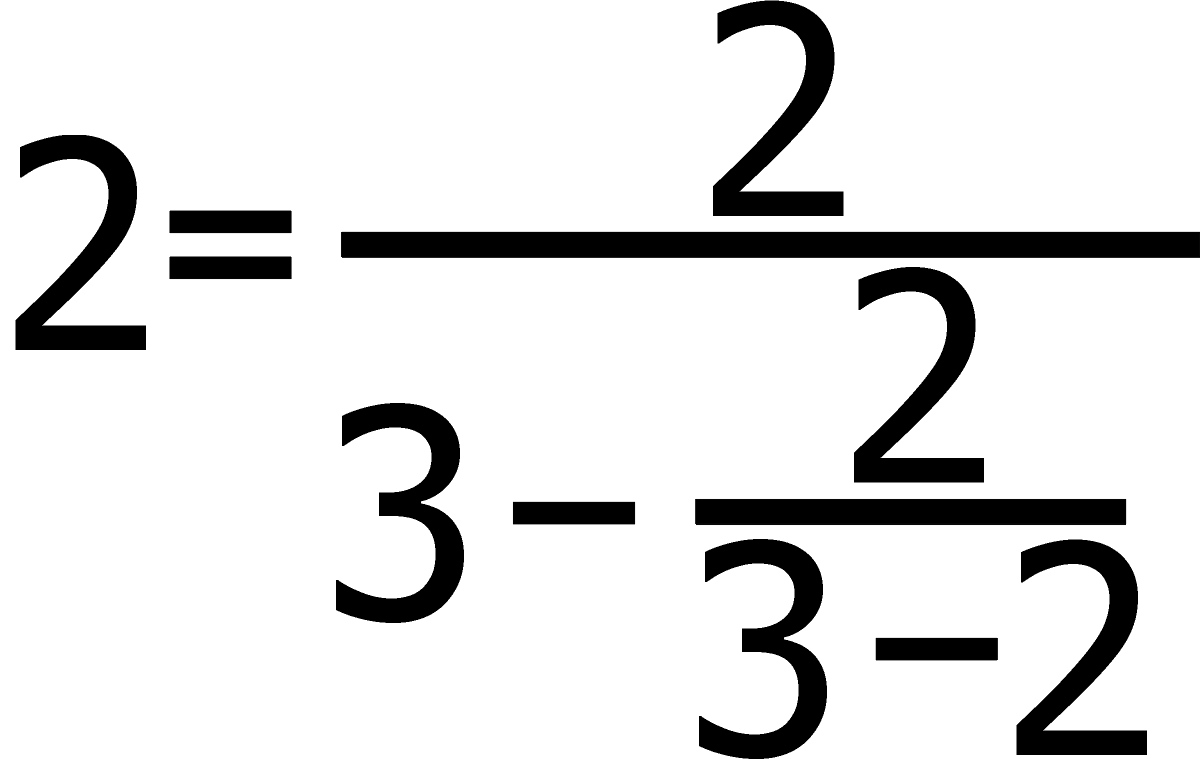
Ponownie wprowadzamy identyczne zastępstwo najniższej dwójki
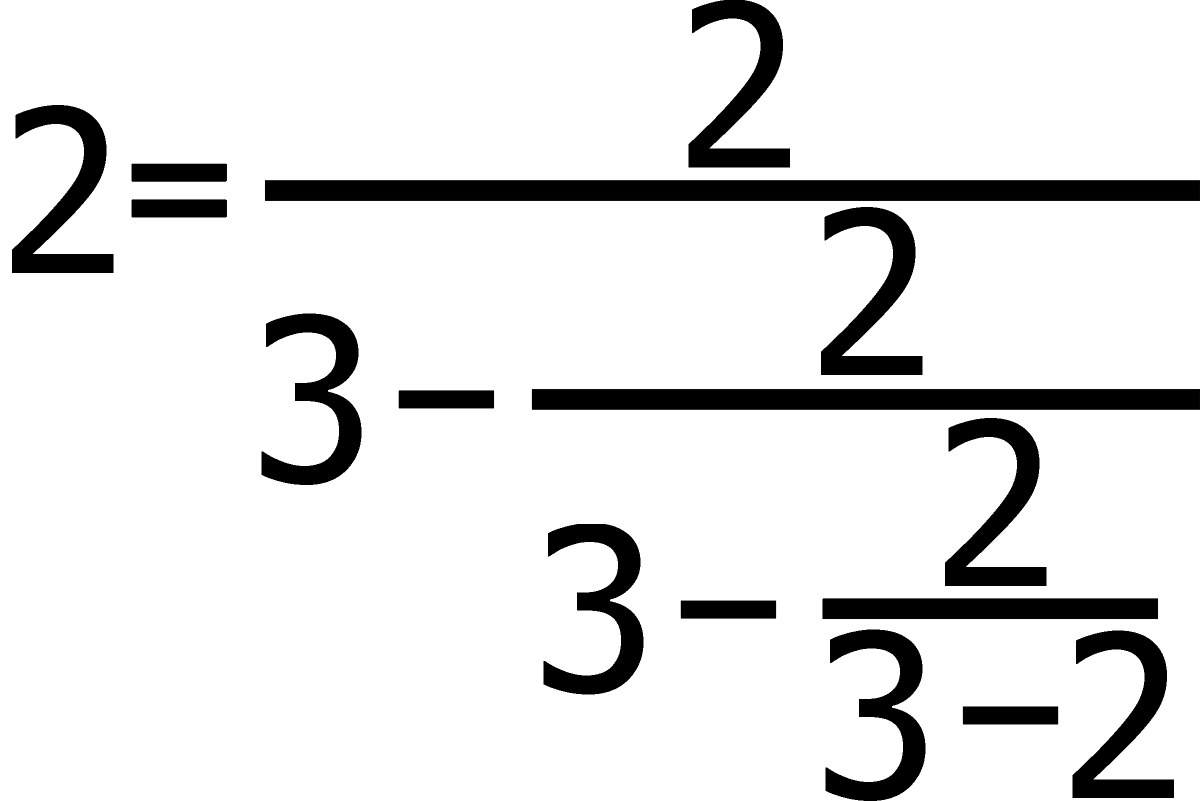
I kontynuujemy taką podmianę w nieskończoność, czyli otrzymujemy
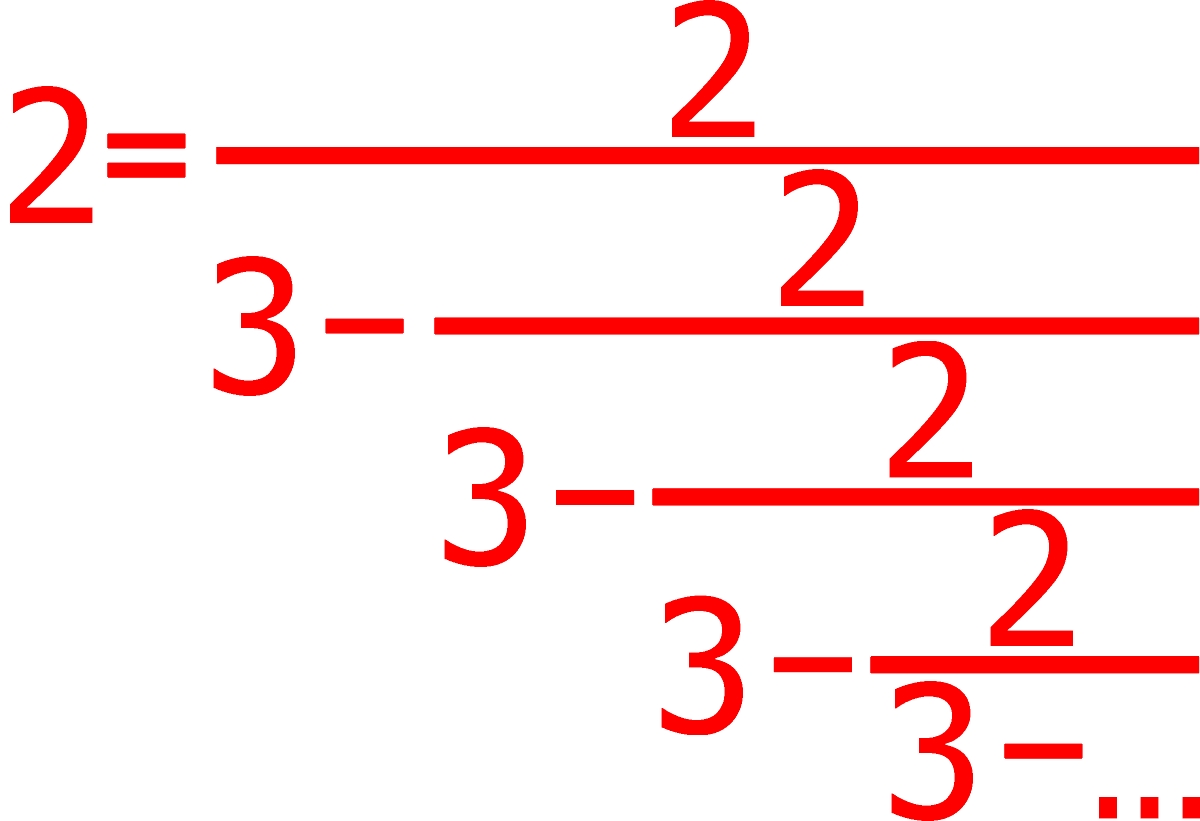
Teraz porównujemy końcówki obu wątków: prawe strony czerwonych równości są jednakowe, zatem lewe także muszą być równe, czyli 1 = 2.
Urok tego sofizmatu tkwi między innymi w zwodniczości cyfry zastąpionej wielokropkiem. Nowicjusze zwykle zwracają na nią uwagę twierdząc, że przecież jest inna. Z niejakim trudem udaje się ich przekonać (zwieść?), że przy podstawianiu w nieskończoność wpływ „wielokropka” na wynik jest praktycznie zerowy. Gdzie zatem tkwi diabeł, czyli wyjaśnienie tego sofizmatu – w szczegółach, czy w jakiejś sprawie zasadniczej?

Komentarze
Mianownik w obydwu równaniach ma postać:
3 – (2/x) = x
co jest prawdziwe dla x=1 albo x=2. Jak sądzę, to jest przyczyna „dysonansu poznawczego”, przez którą cześć po prawej stronie obydwu równań oznaczonych na czerwono może mieć jeden z dwóch wyników. Zatem błąd tkwi w postawieniu znaku równości między (2/x) z pierwszego równania (tam x=2) a (2/x) z drugiego równania (x=1).
„Z niejakim trudem udaje się ich przekonać (zwieść?), że przy podstawianiu w nieskończoność wpływ „wielokropka” na wynik jest praktycznie zerowy” — ???
Chyba z poważnym trudem i co gorsza oszustwami. Może ktoś się podejmie jakiejś próby wykazania, że ciąg jedynek zbiega do 2 lub odwrotnie?
Innymi słowy, wpływ wielokropka nie jest zerowy, tylko opisywany przez jakąś hiperbolę (która w otoczeniu 1 nijak nie chce być zaniedbywalna).
„Nowicjusze zwykle zwracają na nią uwagę twierdząc, że przecież jest inna” i właśnie chyba o tę ostatnią cyfrę w obu przypadkach chodzi. W pierwszym przypadku o to, że ciąg jest zbieżny do 1 (co w sumie daje 2/3-1), a w drugim do 2, co daje (2/3-2) i w ostateczności wychodzi 1 różne od 2.
Aha – co nie zmienia faktu, ze „dowod” jest faktycznie sliczny.
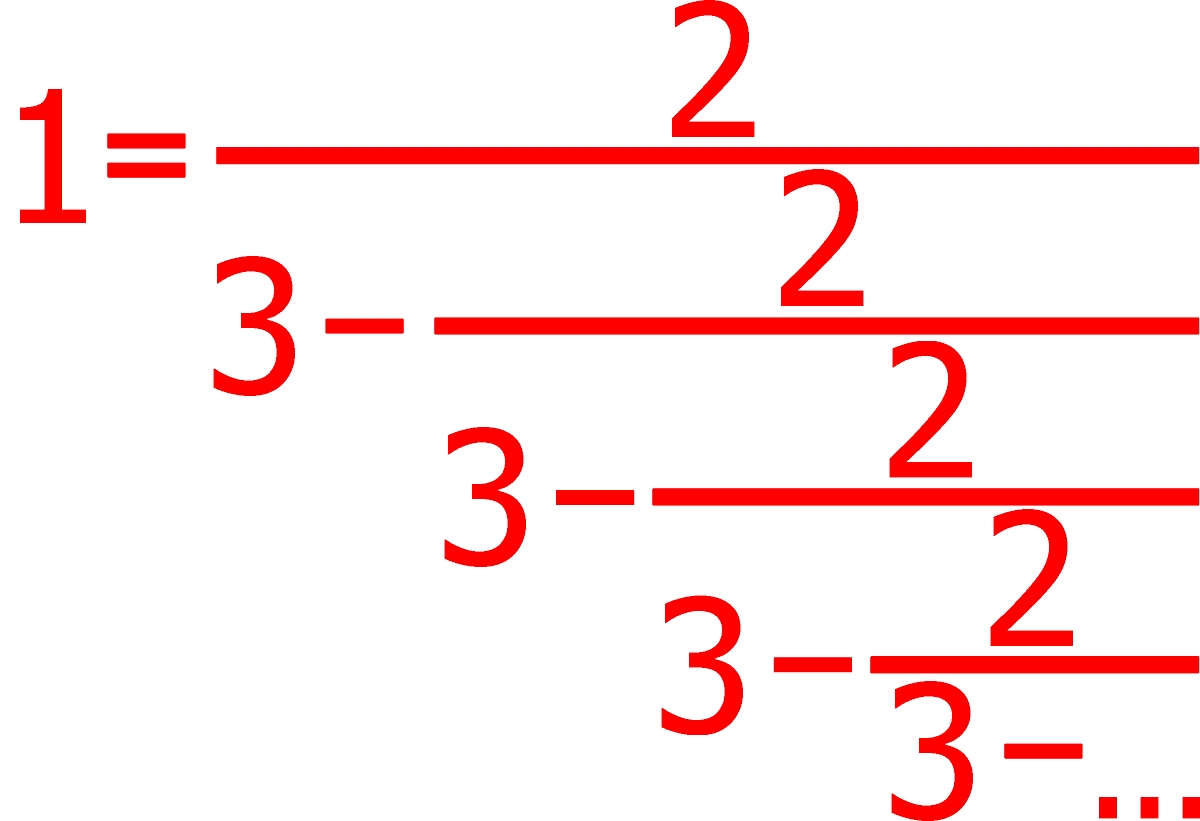
Jeśli wyrażenie:
2
———————
2
3 – —————
2
3 – ———-
3 – …
(chodzi o prawą stronę czerwonych równości)
przyrównujemu do liczby, to proszę mi powiedzieć jaką wartość ma to wyrażenie. 😉
Pozdrawiam,
Jazz_off
Panie Marku!
Jak mam wstawić rysunek do komentarza aby nie wychodziły takie potworki jak w moim poprzednim wpisie? Próba wstawienia pliku bmp czy png kończy się u mnie niepowodzeniem.
PS
Opublikowałem ten wpis, bo może przyda sie innym komentatorom.
Otóż… nie mam zielonego pojęcia. W edycji jest OK, a efekt ostetczny jaki jest każdy widzi. Spróbuję sie dowiedzieć, jak sobie z tym radzić i dam znać dokładnie w tym miejscu. Na razie staram się podpierać „obrazki” komentarzem (kursywa) w komentarzu. (mp)
Obrazki może tak?
. o
.
. /\
Oj, chyba nie tak. Nawet w edycji nie pojawia się nic „obrazkowego”. mp
Wpadlem na ciekawy pomysl:
1^x=1^1
Wiec x=1
1^0=1
1^1=1
1^1=1^0
Wiec 1=0
W ten „sposob” mozna wyglupiac sie dalej:
sin(Pi) = 0 = sin(0)
Wiec Pi = 0 …
Obawiam sie, ze nikt nie da sie nabrac na uzywanie funkcji nie roznowartosciowych…
Sin(Pi)=sin(3,141592653589…)=0,054804…
Rozumiem, ze to byla antyreklama jakiegos pakietu obliczeniowego? Z ciekawosci jakiego, bede wiedzial czego unikac…
Dla porownania Maple’6:
przy domyslnej dokladnosci: sin(3.141592653589)=-.4102067615e-9
po wymuszeniu 15 miejsc po przecinku: .7932384626e-12
Zastanawiam się dlaczego większość kalkulatorów podaje wartość sin(pi)=0, a część (stanowcza mniejszość) podaje 0.054……
Problem jest właśnie w tym wielokropku! W pierwszym przypadku oznacza on granicę ciągu, którego wyrazy są stale równe 1. W drugim przypadku jest to granica ciągu, którego wyrazy są stale równe 2. Nie ma tu żadnej sprzeczności, tylko sposób zapisu ciągu jest „ukryty”.