O Secie
Właściwie powyższy tytuł powinien brzmieć „O grze SET!”. W takiej formie, czyli dużymi literami i z wykrzyknikiem, nazwę gry wypadałoby pisać zgodnie z życzeniem wydawcy. Odmienianie także jest niewskazane, bo to trochę tak, jakby odmieniać okrzyk Eureka! Obiecuję częściową poprawę, czyli czasem zgrzeszę odmianą.
„Szkielet” znanych wszystkim kart do gry stanowią dwie cechy – ranga i kolor. Rang jest 13, kolorów 4. Na każdej karcie oznaczona jest jedna ranga i jeden kolor, czyli w sumie mamy 13 x 4 = 52 karty.
SET! także jest grą w karty, ale specjalne: „szkieletem” są cztery cechy – kształt, kolor, liczba i tło, z których każda może przybierać trzy „wartości”. Mamy więc trzy kształty – romb (r), owal (o), wężyk (w); trzy kolory – czerwony (c), zielony (z), fioletowy (f); trzy liczby – 1, 2, 3 oraz trzy rodzaje wypełnień – jednolite (j), paski (p) i brak wypełnienia (b). Na każdej karcie znajduje się po jednej wartości każdej z czterech cech, czyli w sumie kart jest 3^4 = 81. Oto kilka z nich:

W zasadzie SET! nie jest grą logiczną, choć korzysta się w niej z elementarnego schematu wnioskowania dedukcyjnego (jeżeli…, to…). Stanowi przede wszystkim znakomitą zabawę percepcyjną, a poza tym przypomina niektóre pasjanse.
Na stół wykładany jest tuzin odkrytych kart – kto pierwszy dostrzeże seta, ten głośno mówi „set!” i wskazuje, co zauważył. Jeśli jest to set, odkrywca go zabiera i otrzymuje za spostrzegawczość punkt. Jeśli popełnił błąd, czyli wskazał nie-set, traci punkt. Liczbę wyłożonych kart uzupełnia się do dwunastu, a gdy gracze zgodzą się, że wśród wyłożonych kart nie ma seta, dokładane są trzy kolejne karty. I tak przebiega zabawa, aż do ujawnienia i „rozgrabienia” wszystkich setów, czyli rozdysponowania między grających całej talii. Zwycięzcą zostaje najzasobniejszy w punkty.
Set w grze SET! to trzy karty, na których każda z czterech cech jest taka sama (ma identyczną „wartość”) lub każda jest inna. Poniżej znajduje się pięć tercetów. Które z nich są setami, a które nie – to wprawka-zagadka.
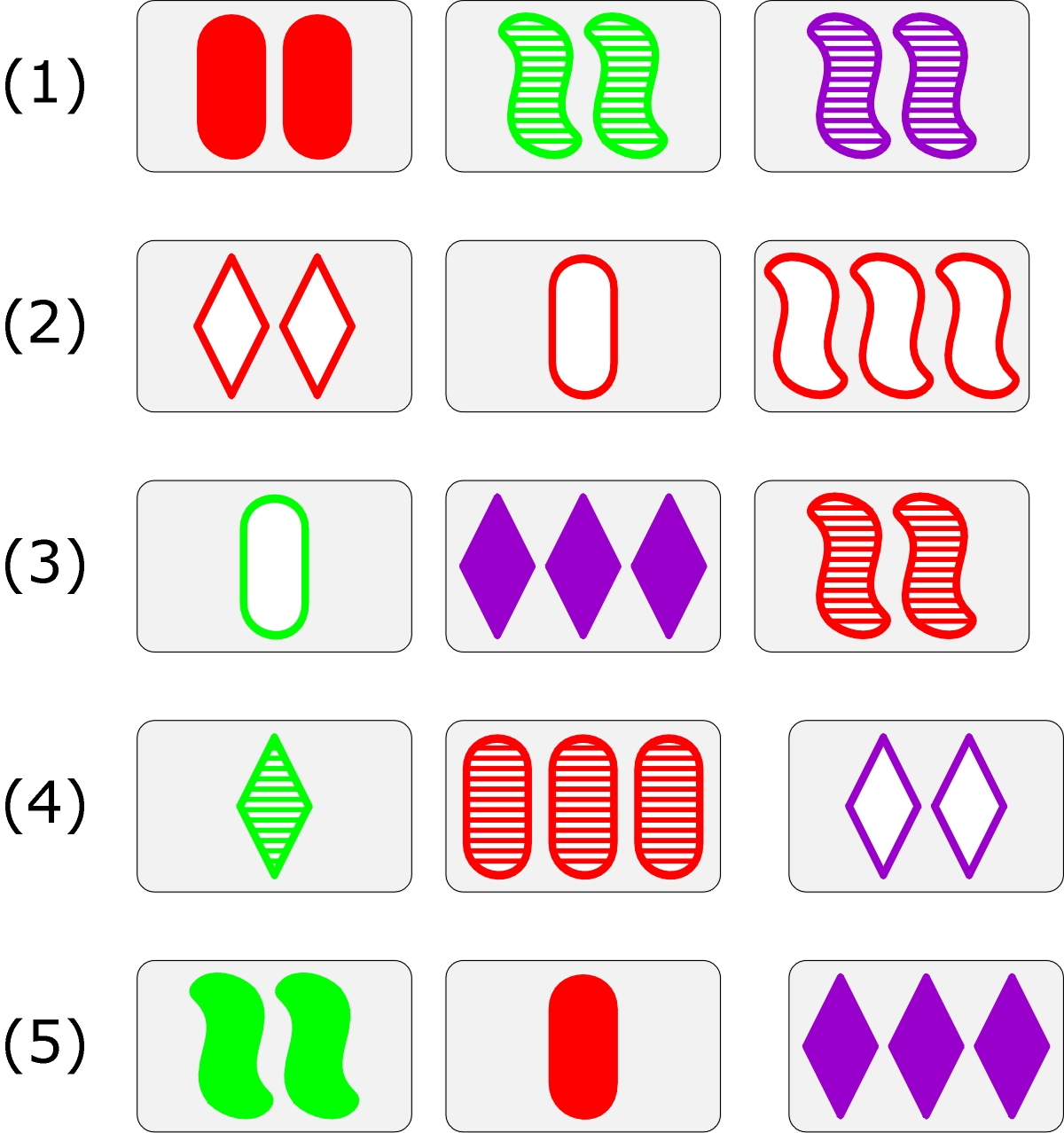
Szukając setów można stosować proste „strategie”, przypominające systematyczne przeszukiwanie z eliminacją i dobieraniem według kryteriów, którymi są cechy i ich konkretne wartości. W praktyce jednak najlepszymi graczami okazują się często dzieci, które żadnych strategii nie stosują, za to mają bystry i „giętki” wzrok i umysł.
Do popularności SETa w dużym stopniu przyczyniła się struktura talii, stanowiąca ciekawy model matematyczny (zbiór 4-elementowych krotek liczbowych o elementach należących do zbioru {0,1,2}). Rzec by można, iż jest to obiekt „treningowy”, umożliwiający analizowanie i prezentację wielu zagadnień związanych z kombinatoryką i teorią zbiorów, zwłaszcza w kontekście problemów obliczeniowych i optymalizacyjnych. Trochę informacji na ten temat można znaleźć na stronie firmowej gry.
Zanim dorobiłem się oryginalnej talii, korzystałem z kart własnego pomysłu i wyrobu, wzorowanych na zadaniu o wypożyczalni japońskich aut. Cechy stanowią: marka auta, typ nadwozia, kolor i tapicerka. Trzem markom – Honda, Nissan i Subaru – odpowiadają litery H, N, S (zamieniłem Toyotę na Subaru, bo S jest S-em dla obu graczy siedzących naprzeciw siebie). Nadwoziem jest krój liter – zwykły, ozdobny (szeryfy) i kursywa. Trzy kolory to różowy, niebieski i żółty; tapicerka jest w paski, w kratkę lub bez deseniu. Poniższa łamigłówka, a raczej „łamioczko”, przedstawione jest w wersji samochodowej.
W trakcie gry powstała nietypowa sytuacja. Wśród tuzina wyłożonych „liter-aut” nie było żadnego seta. Dodano zatem trzy i okazało się, że… nadal nie ma seta. Pojawiły się więc trzy następne litery i teraz parking zastawiony był osiemnastoma japońskimi autami.

Wreszcie można było znaleźć sety, ale łamigłówka nie polega bezpośrednio na ich wskazaniu. Proszę podać numery aut, które trafiły na parking jako trzy ostatnie, jeśli wszystkie one znajdują się w tym samym rzędzie.
Rozwiązania można nadsyłać w komentarzach do wtorkowego południa (1 kwietnia), a do rozlosowania jest SET! Oczywiście komentarze z rozwiązaniami nie będą przedwcześnie ujawniane.

Komentarze
Na początku dziękuję Panie Marku za przypomnienie wspaniałych studenckich czasów i wielu godzin spędzonych przy tej grze z osobami z mojej grupy. Pamiętam wykładowców, którzy musieli czekać z rozpoczęciem zajęć do czasu, aż my skończymy partię seta i pierwszą talię kart do seta, narysowaną na jakimś bloku technicznym.
Przechodząc do zadań:
Sety są w zestawach 2,3 i 5.
W zestawie 1 mamy tylko dwie karty z wężykami i tylko dwie karty z zakreskowanym tłem
W zestawie 4 mamy tylko dwie karty z rombem i tylko dwie karty z zakreskowanym tłem.
Łamigłówka:
Wśród narysowanych symboli można znaleźć takie sety:
3,7,11
2,3,14
5,15,18
5,8,17
6,9,11
Ponieważ trzy ostatnio dołożone karty są w jednym rzędzie musi to być rząd pierwszy. (Gdyby te karty były w rzędzie drugim, to drugi set leżałby na stole przed dołożeniem tych kart; gdyby te karty były w rzędzie trzecim, to piąty set leżałby wcześniej na stole)
Skoro trzy dołożone karty są w pierwszym rzędzie, to karty o numerach 7-18 musiały leżeć na stole wcześniej.
Zatem na stole nie mogło być karty numer 5 (bo byłby na stole set trzeci i czwarty), karty numer 6 (byłby set piąty) oraz karty numer 3 (byłby set pierwszy).
Zatem trzy ostatnio dołożone karty to karty: 3, 5, 6.
A na koniec małe zadanie ode mnie:
W czasie gry niezbyt często udaje się dopasować w sety wszystkie karty, część z nich zostaje wtedy na stole. Najczęściej na stole zostaje 9 lub 12 kart. Łatwo można zauważyć, że liczba kart, które zostają na stole musi być podzielna przez 3. Czy na stole mogą zostać dokładnie trzy karty, które nie tworzą seta?
Tak sformułowany tytuł wpisu może być kłopotliwy z jeszcze jednego powodu:
Zwolennicy mocniejszych trunków mogliby spodziewać się po nim nieco innej treści (i duża litera „S” im w tym nie przeszkodzi). 🙂
Pozdrawiam
AB
Jako ostatnie pojawiły się samochody o numerach: 3, 5 oraz 6.
Wprawka:
Sety: 2, 3, 5
Nie-sety: 1,4
Zagadka konkursowa:
Jako trzy ostatnie, na parking trafiły auta 3, 5 i 6.
Rozwiązanie:
Zaczęłam od znalezienia setów, jest ich 5:
5-8-17
3-7-11
6-9-11
2-3-14
5-15-18
Dopiero ostatnie trzy karty spowodowały, że jakiekolwiek sety się znalazły, stąd wniosek, że co najmniej jedna z nich musi należeć do kilku setów (w dodatku zakładam, że każda z tych trzech dołożonych jako ostatnie należy do któregoś z setów, bo inaczej zagadka miałaby wiele odpowiedzi).
Ponieważ wszystkie trzy karty muszą w dodatku leżeć w tym samym rzędzie, stąd:
– na pewno nie są to karty z rzędu trzeciego (14, 15, 17 i 18 należą tylko do trzech setów, zatem dwa pozostałe sety musiałyby w pozostałych 15 kartach już wcześniej być)
– nie są to karty z rzędu drugiego, gdyż set 2-3-14 nie ma tam żadnej karty, więc także musiałby być w tych wcześniejszych piętnastu kartach
– w pierwszym rzędzie są dwie karty: 3 i 5, z których każda należy do dwóch setów, a wszystkie te cztery sety są „rozłączne”, poza nimi są też 2 i 6, każda należy do dokładnie jednego seta. Odpowiedzią mają być trzy karty, zatem są to na pewno 3 i 5. Trzecią nie może być 2, bo jej seta (2-3-14) eliminuje już zabranie karty 3, a w pozostałych piętnastu nadal pozostawałby set 6-9-11. Zatem trzecią dołożoną kartą jest 6.
Dla mnie, osoby znającej SETa wcześniej (znajomi mieli karty własnej roboty), zadanie wcale nie było takie proste. Przyzwyczaiłam się już do standardowego wyglądu kart tak, że zamieszczone tu symbole były dla mnie zupełnie nieczytelne, przede wszystkim chyba przez cechę-krój litery. Czułam się, jakbym grała po raz pierwszy 🙂
Zwykle graliśmy nieco inaczej: wykłada się dwanaście kart, w razie braku seta dokłada się jedną, a gdy dalej nie ma – kolejną itd. Sety po prostu się zbiera, kto pierwszy, ten lepszy. Jeśli dwie osoby rzucą się naraz do tego samego seta, muszą się nim podzielić – jedna bierze jedną kartę, druga drugą, a trzecia karta zostaje na stole. Gdy będą to trzy osoby – każdy dostaje po jednej. Nie zdarzyło nam się chyba, aby więcej osób niż trzy usiłowało zabrać tego samego seta ;). A jaką satysfakcję czwartej osobie przynosi sytuacja, gdy trzy inne muszą się podzielić jednym, a ona zbiera całego, rozłącznego z tamtym seta, którego nikt inny nie zauważył!
Z początkującymi graliśmy czasem na „apsik!-i” (słowo dobre jak każde inne). Gdy ktoś z zaawansowanych graczy widział seta, mówił „apsik!” i liczył do dziesięciu lub piętnastu, jeśli w ciągu tego czasu początkujący znalazł tego seta, to go zabierał, jeśli nie, zabierał go ten, kto znalazł go pierwszy.
Dla urozmaicenia, utrudnialiśmy czasem grę, wprowadzając wymóg zdejmowania tylko dwóch rozłącznych setów naraz albo dodając piątą cechę – położenie. W tej wersji, rozkłada się 27 kart w trzech grupach 3×3. Również pod względem położenia karty muszą tworzyć set – czyli albo wszystkie powinny być z jednej grupy, albo każda z innej. Gdy seta nie ma, również dokłada się jedną kartę, do dowolnie wybranej grupy, ale równomiernie. Ta wersja SETa została kiedyś zresztą przez kogoś nazwana bodajże super-SETem.
A’propos, wykrzyknik w nazwie występuje chyba tylko w niemieckiej wersji tej gry, produkowanej przez Ravensburgera, ale mogę się mylić.
Pozdrawiam!
Fajnie najato, że wspomniałaś o „ulgach” dla początkujących, którzy mogą się łatwo zniechęcić do SETa, grając z rutyniarzami. Zwykle tylko patrzą jak inni sprzatają im wszystko sprzed nosa i przegrywają sromotnie. Więc przychylam się do dawania początkującym fory, np. w takiej formie, jak napisałaś.
Zz
Witam,
Myślę że jako ostatnie doszły auta o numerach 3, 5 i 6
PS. Ja podobnie jak najata bardzo już przywykłam do „zwykłego” seta. Sama zresztą robiłam swoją pierwszą talię – flamastrami, ale od wyciętych wcześniej przeze mnie szablonów i może jako tako było równo:) Drugą i ostatnią talię też produkcji ręcznej ale już przy użyciu bardziej zaawansowanych technik (drukarka, foliowanie…) dostałam od znajomych:)
Po „apsiku” długo, długo nic i wreszcie: 3,5,6.
Pozdrawiam
Moje rozwiązanie to auta 3 , 5 i 6 .
Z informacji , że ostatnio przybyłe auta są w jednym rzędzie i z obecności Seta 3+7+11 można wywnioskować , że ostatnia trójka nie dołączyła do trzeciego rzędu . Z Seta 5+15+18 można wywnioskować , że ostatnia trójka nie dołączyła do drugiego rzędu . A zatem trzy ostatnie auta dojechały do pierwszego rzędu (jednym jest auto 3 , a drugim 5) .
Z Seta 6+9+11 możemy zidentyfikować trzecie auto z ostatnio przybyłych , czyli 6 .
Inne Sety , które można zauważyć (np 2+3+14) nie są tak cenne dla analizy prowadzącej do znalezienia rozwiązania , ponieważ nie pozwalają na sformułowanie dostatecznie „twardych” wniosków .
Dziękuję i pozdrawiam
AC
Jako ostatnie na parking trafiły samochody 3,5,6.
Zadanie pośrednio wymagało odnalezienia wszystkich Set-ów, a jest ich pięć: 2-3-14; 5-8-17; 6-9-11; 3-7-11; 5-15-18.
Spośród tych kart trzeba było znaleźć trzy w jednym rzędzie, które wyeliminują wszystkie pięć Set-ów, ale to już prosta zabawa.
Muszę się przynać, że „wymiękłem” na samochodach i przerysowałem karty na normalne Set-owe, pokolorowałem kredkami razem z córeczką i wtedy wspólnie, szybko odnaleźliśmy wszystkie Sety. Dlaczego z córką? Bo te kilka razy, kiedy mieliśmy okazję grać w Set-a, zawsze była nie do pokonania – dzieci są chyba w tych spostrzegawczych grach o wiele lepsze i sprytniejsze (teraz też było trzy do dwóch dla niej).
Sety tworzą następujące trójki samochodów:
2, 3, 14
3, 7, 11
5, 15, 18
5, 8, 17
6, 9, 11
Jako ostatnie trafiły na parking auta nr 3, 5, 6 z pierwszego rzędu.
Pozdrawiam
AB
PS: Dobrze, że samochody te stoją na parkingu, bo po secie jazda raczej nie jest wskazana. 😉
3,5,6