Bezcenne
Konkursowy Hexa-Trex okazał się prostszy, niż przypuszczałem. Przede wszystkim ze względu na dzielenie, które wygląda na działanie kluczowe w tego typu zadaniach, jeżeli oczywiście występuje.
Kilka uwag zawartych w komentarzach sprawiło, że postanowiłem z tą łamigłówką jeszcze się nie rozstawać, pojawił się bowiem ciekawy problem, dotyczący Hexa-Trexów „kompletnych”, czyli zawierających, jak konkursowy, wszystkie różne znaki (cyfry oraz symbole działań i równości) – każdy dokładnie raz. Pierwszą inspiracją był komentarz Bo: „czym wyższy jest poziom, tym robi się ciekawiej, gdyż zawsze trzeba znaleźć jedno rozwiązanie„. Otóż właśnie: na ogół układając łamigłówkę należy pilnować, by nie miała więcej niż jednego rozwiązania. Kompletny Hexa-Trex jest natomiast zadaniem, przy którym trzeba by się bardzo postarać, aby rozwiązania były przynajmniej dwa. Jak bardzo? Sądzę, że ułożenie takiej łamigłówki z dwoma całkiem różnymi rozwiązaniami (a nie tylko częściowo, na przykład w związku z przemiennością działań – jak mnożenie w konkursie) jest przedsięwzięciem karkołomnym.
Teoretycznie sprawa wygląda tak: z siatki trójkątnej, traktowanej jako graf, „wycinamy” 15-wierzchołkowy podgraf mający co najmniej dwie ścieżki hamiltonowskie, a w jego wierzchołkach rozmieszczamy 10 różnych cyfr i pięć różnych znaków działań i równości tak, aby kolejne cyfry i znaki na dwóch różnych ścieżkach tworzyły poprawne równości. Ponieważ liczba możliwych podgrafów i rozmieszczeń jest astronomiczna, więc w praktyce „zabawa” polega na ułożeniu dwóch równości i próbach wpasowania ich w jeden wspólny graf. Równości te powinny spełniać określone warunki. Jakie? Nawet gdybym potrafił te warunki sprecyzować, to obawiam się, że przejście od teorii do praktyki byłoby nadzwyczaj trudne. Mógłbym ogłosić konkurs na ułożenie takiego zadania, ale nie dysponuję, niestety, odpowiednio wartościową nagrodą.
Jeden z najwybitniejszych matematyków XX wieku i nietuzinkowa osobowość, Paul Erdös, miał zwyczaj wyceniać problemy do rozwiązania. Mówił na przykład: „uporanie się z tym zagadnieniem warte jest 100 dolarów” – i z reguły wypłacał ustalone honorarium delikwentowi, który na nie zasłużył. Zastanawiałem się, za ile podjąłbym się ułożyć kompletny Hexa-Trex z dwoma różnymi rozwiązaniami. Na pewno nie za 100 dolarów, ale trudno określić, za ile, bo pracochłonności nie potrafię ocenić i nie mam pewności, czy w ogóle bym się z tym uporał. Krótko mówiąc, takie układanie jest bezcenne. Zatem spróbowałem za darmo, a efekt parogodzinnych zmagań znajduje się poniżej. O tym, że do konstrukcyjnej poprawności daleko, czyli w gruncie rzeczy nie jest to Hexa-Trex, świadczą czerwone linie – cyfry i znaki w polach, które łączą, także mogą być kolejnymi w równościach. Czy znalezienie obu rozwiązań będzie równie łatwe jak jednego w łamigłówce konkursowej?
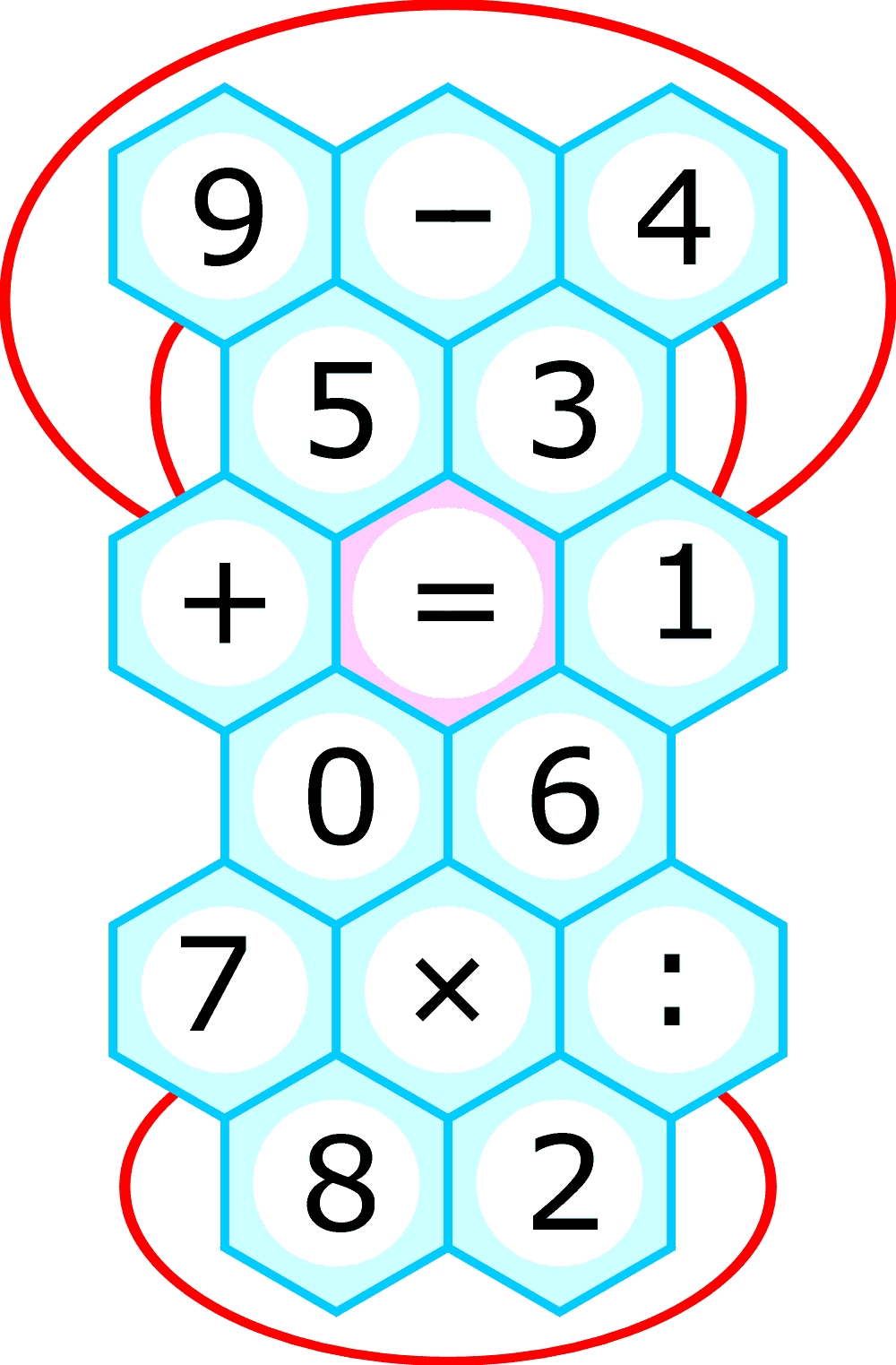
Za poprawne rozwiązanie konkursowego Hexa-Trexu grę QUIXO, otrzymuje Robert_C. Laureata proszę o kontakt pod adresem m.penszko@polityka.com.pl w celu ustalenia sposobu przekazania nagrody.
PS Poniżej pierwszy kompletny Hexa-Trex z dwoma kompletnie różnymi rozwiązaniami, autorstwa Pana Roberta_C (szczegóły w komentarzu).
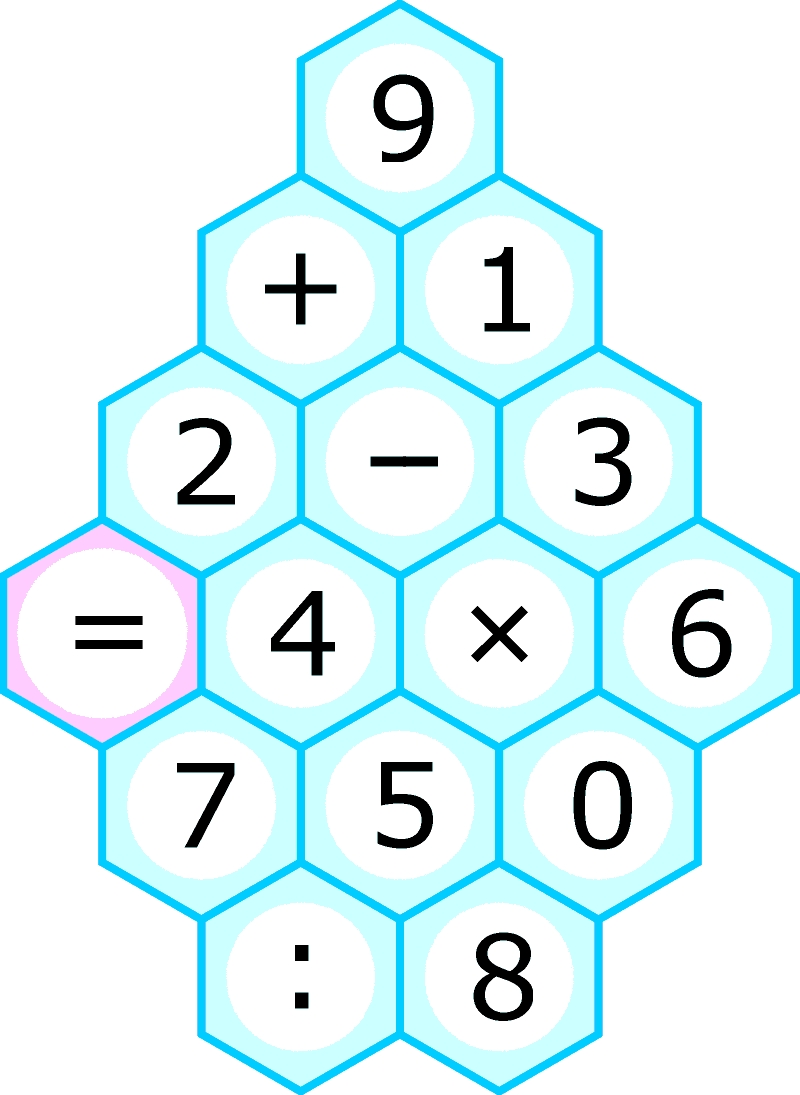

Komentarze
To zadanie, trzeba przyznać, było zdecydowanie trudniejsze. Po pierwsze: do znalezienia były dwa rozwiązania, po drugie: zestawienia pól połączonych czerwonymi liniami nie są (w podświadomości) tak oczywiste i łatwo którąś możliwość przeoczyć i po trzecie – najistotniejsze: dzielenie można było wykonać na (absolutnie bez przesady) kilkadziesiąt sposobów.
A dodatkowo okazało się, że rozwiązań to jest siedem!
43-59+16 = 0x82:7
43-59+16 = 0x87:2
43-59+16 = 0x2:78
43-59+16 = 0x7:28
4-9+5 = 0x287:613
4-9+5 = 0x782:613
41+9-35 = 60×7:28
Nawet jeśli uznać, że cztery pierwsze to tylko mutacje jednego, a piąte i szóste – drugiego, to i tak mamy nie dwa, a trzy całkowicie różne rozwiązania.
„Ręcznie” udało mi się odnaleźć trzy ostatnie, przy pierwszej czwórce pomógł mi komputer.
Pozdrawiam
AB
W moim wcześniejszym komentarzu z rozwiązaniami, który zostanie ujawniony pewnie za kilka dni, napisałem, że rozwiązań tej łamigłówki jest trochę więcej. A wszystkiemu winne jest… zero.
Wydaje mi się, że jeśli nie zrobimy pewnych dodatkowych założeń (o czym dalej), to utworzenie Hexa-Trexu mającego dwa rozwiązania (a może i więcej) wcale nie musi być takie trudne. W tej kwestii chyba trochę nie docenił Pan potęgi zera, Panie Marku.
W matematyce zero wcale nie musi być „zerem”. 😉
Cyfra ta bowiem, jeśli wystąpi samodzielnie (jako cała liczba), może nam „załatwić” sprawę innych, w danej chwili niepotrzebnych i przeszkadzających cyfr, których nijak nie można dopasować do równości.
Udało mi się stworzyć pewien schemat ogólny, który gwarantuje przynajmniej dwa całkowicie różne rezultaty:
Wygląda to mniej więcej tak:
_ 0a b c
_x : – + =
d e f g h i
__0_A_B_C
_x_ :_-_+_=
D_E_F_G_H_I
Ponieważ obawiam się, że może się rozjechać, to przedstawiłem to w dwóch wersjach i na wszelki wypadek jeszcze krótki opis:
Trzy rzędy hexów: w pierwszym – 4 pola, w drugim – 5 i w trzecim – 6. W pierwszym polu pierwszego rzędu – zero, a dalej trzy prawie dowolne cyfry (jaki muszą spełniać warunek – za chwilę). W drugim rzędzie mamy same znaki działań – po kolei: „x”, „:”, „-„, „+”, „=”. Wreszcie w trzecim – sześć pozostałych cyfr.
Możliwe są następujące równości:
1. d x 0 : abc = ih + g – fe
2. de x 0 : fghi = c + b – a
Do tego dochodzą mutacje:
2a. ed x 0 : fghi = c + b – a
2b. d x 0 : efghi = c + b – a
Łatwo zauważyć, że lewa strona zawsze jest równa zero. Wystarczy zatem, aby cyfry spełniały warunki:
ih + g – fe = 0,
c + b – a = 0
i oczywiście żeby były różne. Ułatwi nam to fakt, że „d” może być całkowicie dowolne.
Można to uzyskać na wiele sposobów, np:
a=9, b=6, c=3, d=4, e=5, f=2, g=7, h=8, i=1
Diagram wygląda wtedy „mniej więcej” 😉 tak:
__0_9_6_3
_x_ :_-_+ =
4_5_2_7_8_1
Rozwiązania (dwa podstawowe):
4×0:963 = 18+7-25
45×0:2781 = 3+6-9
Wracając do wyników ogólnych, to dość prawdopodobne, że może ich być więcej (zawsze też można zamienić ze sobą wartości „b” i „c”) – szczerze mówiąc nie starałem się szukać dalej.
Ważne natomiast jest to, że w podstawowych rozwiązaniach, poza zerem, wszystkie liczby tworzące równości są całkowicie różne! Nie można zatem powiedzieć, że jedno jest pochodną drugiego.
Oczywiście zgodzę się z tym, iż taka postać łamigłówki może nie być zbyt ciekawa dla rozwiązującego i pewnie, Panie Marku, nie całkiem o to Panu chodziło.
Dlatego też wydaje mi się, że aby tego uniknąć, to należałoby dodać, o czym wspominałem wcześniej, pewne dodatkowe założenie.
Pierwsza wersja – jako dodatkowa zasada dla rozwiązującego: zero nie może występować samodzielnie (wyłącznie jako składnik liczby wielocyfrowej).
Wersja druga (mniej rygorystyczna) – jako instrukcja dla autora zadania: zero nie może występować w bezpośrednim sąsiedztwie znaków mnożenia i dzielenia. W tej sytuacji dodatkowa zasada (wspomniana jako pierwsza) nie będzie konieczna. Aczkolwiek może być trudniejsze tworzenie łamigłówki.
Jeśli wprowadzimy którąś z tych zasad unikniemy nadmiernego (i trudno kontrolowalnego) wzrostu niechcianych, nieciekawych rozwiązań.
Oczywiście w takiej sytuacji problem ogólnego schematu wielorozwiązaniowego Hexa-Trexu pozostaje otwarty.
Pozdrawiam
AB
Pierwsze rozwiązanie to :
7/28×60+1=59-43
I tym samym mój argument , że kiedy jest tylko jedno dzielenie to musi dawać wynik całkowity , oczywiście upada !
Na szczęście dokładnie przeczytałem początek wpisu i „uwagi w komentarzach ” oraz „pierwsza inspiracja” włączyły mi światełko alarmowe , co pozwoliło szybko zweryfikować moje niesłuszne twierdzenie .
Oczywiście spróbuję znaleźć również drugie rozwiązanie.
Pozdrowienia
AC
Z pierwszych komentarzy (wszystkie uwolnię pojutrze) wynika, że pseudo-Hexa-Trex jest mniej udany, niż przypuszczałem, ma bowiem przynajmniej… dziewięć rozwiązań, choć można je połączyć w grupki bliźniacze. Wydaje się, że gdyby zabawę traktowac nieco poważniej, wypadałoby doprecyzować, co oznacza określenie „całkiem różne rozwiązania”.
mp
Znalazłam takie rozwiązania:
7:28×60+1=59-43
16:28×70=35+9-4
41+9-35=60×7:28
Okazało się, że ten Hexa-Trex ma więcej niż dwa rozwiązania. Zaciekawiony ile ich tak naprawdę jest, postanowiłem to sprawdzić. Oczywiście musiałem tym razem poprosić o „pomoc” komputer, bo sam, nawet z pomocą syna, bym nie dał rady.
Oto chyba wszystkie możliwe rozwiązania:
– takie, które są znacząco różne
9+16/28*70=53-4
4-9+16/28*70=35
41+9-35=60*7/28
41+9-35=6/28*70
16/28*70=35+9-4
7/28*60+1=59-43
59-43=6/28*70+1 i w drugą stronę 6/28*70+1=59-43
– takie, gdzie mnożenie przez 0 daje wiele podobnych układów:
4-9+5=316/287*0
4-9+5=316/782*0
4-9+5=0*782/613
4-9+5=0*287/613
43-59+16=0*7/28
43-59+16=0*87/2
43-59+16=0*82/7
43-59+16=0*2/78
5=316/287*0+9-4
5=316/782*0+9-4
7/28*0+16=59-43
7/28*0+59-43=16
87/2*0+16=59-43
87/2*0+59-43=16
82/7*0+16=59-43
82/7*0+59-43=16
2/78*0+16=59-43
2/78*0+59-43=16
– i jeszcze takie mniej eleganckie, z cyfrą 0 na początku:
34-59+078*2/6=1
1=34-59+078*2/6
078*2/6=1+59-34
Rozwiązań wyszło dużo.
Postanowiłem idąc za ciosem znaleźć „komputerowo” takiego Hexa-Trexa, gdzie byłyby dokładnie dwa rozwiązania. Spróbowałem w oparciu o kształt z pierwszego zadania, czyli:
8
x-
034
1672
+=:
95
Takich układów okazała się być ogromna ilość, więc przedstawię dla przykładu tylko dwa:
9
+1
2-3
=4×6
750
:8
Dokładnie dwa rozwiązania to: 3×608:57=24-1+9, 805:7=42+91-3×6
9
+1
2-3
=475
8x/
06
Dokładnie dwa rozwiązania to: 375/60×4-19+2=8, 375/60×8=42-1+9
Panie Robercie, pierwszy z dwóch przykładów jest idealny, bo niezależnie od tego, jak rygorystyczne byłyby warunki określające odmienność dwóch rozwiązań, to ten przykład z pewnością je spełni (w drugim przykładzie powtarza się dzielenie takich samych liczb).
A zatem to pierwszy kompletny Hexa-Trex z dokładnie dwoma kompletnie różnymi rozwiązaniami. Postanowiłem zaprezentować go w całej okazałości we wpisie jako PS.
Reasumując, jednak przesadziłem wyceniając szukanie przykładów takich zadań na więcej niż 100$.
Pozdrawiam
mp