Rodos wirtualnie
W ciągu minionych siedmiu lat Piotr Murdzia tylko raz, w roku 2003, wrócił z mistrzostw świata w rozwiązywaniu zadań szachowych bez medalu. Poza tym wyjątkiem trzykrotnie było złoto, dwa razy srebro, a niespełna dwa tygodnie temu, na 31 World Chess Solving Championship w Grecji, nasz arcymistrz uzupełnił swój dorobek o brąz. W Mistrzostwach na wyspie Rodos uczestniczyło 84 zawodników z 23 krajów. Wyniki indywidualne i drużynowe, a także zdjęcia, można obejrzeć na stronach: współorganizatora imprezy – Stałej Komisji Kompozycji Szachowej FIDE oraz Polskiego Związku Szachowego.
Turniej WCSC składa się z sześciu rund, każda obejmuje trzy zadania jednego rodzaju. Są to, kolejno: pierwszego dnia – dwuchodówki, trzychodówki, studia; drugiego – maty pomocnicze, wielochodówki, samomaty.
Zadania szachowe stanowią w gruncie rzeczy szczególny rodzaj wieloetapowych łamigłówek. W związku z tym byłoby ciekawe sprawdzić, jak najlepsi puzzlerzy, czyli niejako wieloboiści, startujący na przykład w World Puzzle Championship, wypadliby w szachowej konkurencji na tle specjalizujących się w niej solwerów. Gdyby pozostać przy lekkoatletycznej analogii, wypadałoby przewidywać, że raczej kiepsko, podobnie jak wyniki dziesięcioboistów, np. w skoku o tyczce, nie umywają się do rezultatów tyczkarzy.
Jest niemal pewne, że najlepsi łamigłówkarze nieszachiści byliby bez szans w jednej ze wspomnianych podkonkurencji – studiach, a także w wielochodówkach. W tych specjalnościach bardzo istotną rolę odgrywa bowiem doświadczenie wyniesione z gry – większość solwerów to znakomici, utytułowani szachiści. Tegoroczny mistrz świata, Anglik John Nunn, jest trzecim graczem w swojej ojczyźnie. Jednak z drugiej strony nie brak wyjątków. Na przykład jest niemal sensacją i silnym argumentem przemawiającym na korzyść łamigłówkarzy, że Georgij Jewsiejew, czyli aktualny wicemistrz świata i pierwszy na liście rankingowej, nie jest wcale klasyfikowany jako gracz! Ośmieliłem się nawet półżartem zapytać Piotra Murdzię, czy Rosjanin w ogóle umie grać w szachy. Na serio pytanie jest retoryczne i bezsensowne, ale siła gry Jewsiejewa pozostaje zagadką.
O ile wiem, wśród zaglądających do Łamiblogu jest wielu tęgich główkołamaczy, mam więc nadzieję, że przynajmniej niektórzy skuszą się na sprawdzian, jak wypadliby na Rodos. Nadarza się po temu okazja, bo dzięki uprzejmości Piotra Murdzi dysponuję trzema zadaniami z tegorocznych Mistrzostw. Sprawdzian będzie fragmentaryczny, bowiem zadania pochodzą tylko z pierwszej rundy i są jednego, względnie prostego rodzaju – stwarza to łamigłówkarzom większe szanse, by dorównać solwerom. Dodatkowym handicapem będą zapewne dysponować te osoby, które przynajmniej w miarę regularnie grywają w szachy.
Przed wirtualnym startem w pierwszej rundzie proponuję zainteresowanym krótki trening – dwuchodówkę z Mistrzostw Świata sprzed dwóch lat.
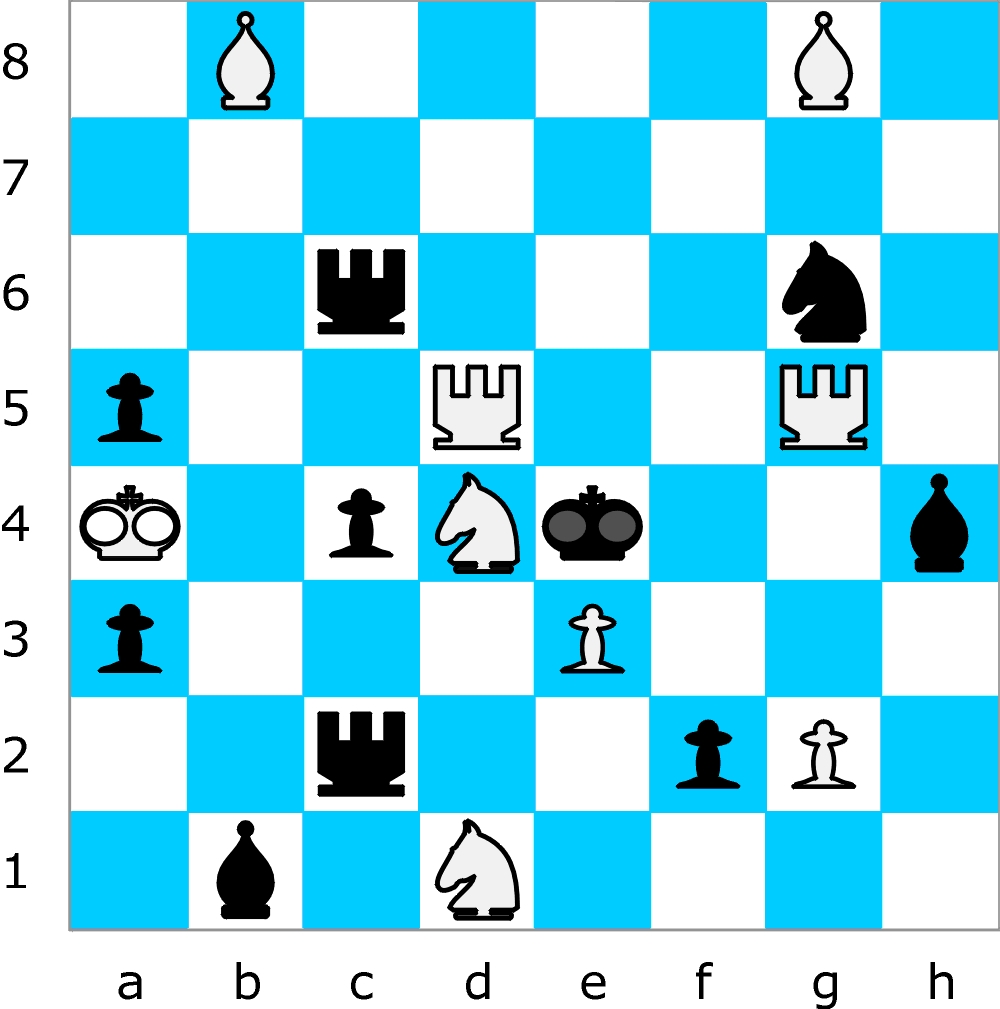
Wystarczy wskazać ruch białych, zapewniający im zwycięstwo w drugim posunięciu.
Kolej na tercet mistrzowskich zadań. Wszystkie są dwuchodówkami, a w każdej wystarczy podać posunięcie, gwarantujące białym wygraną w drugim ruchu.
Uczestnicy Mistrzostw mieli na uporanie się z tymi trzema zadaniami 20 minut. Czy komuś z Państwa uda się zmieścić w tym czasie? A może ktoś okaże się szybszy od najlepszego w pierwszej rundzie Marka Erenburga z Izraela (15 minut).
Niezależnie od tego poprawne rozwiązanie w ciągu 20 minut jednego zadania będzie oznaczać zajmowanie w Mistrzostwach Świata po pierwszej rundzie 61 miejsca, a rozwiązanie dwóch zadań to 40 miejsce, czyli lepiej niż połowa stawki!
Nadsyłane rozwiązania zostaną uwolnione po 48 godzinach od startu, który nastąpił – zgodnie z zapowiedzią – 29 października o godzinie 19.00. Wówczas okaże się, kto był najszybszy i czy rodyjski kwadrans został poprawiony.

Komentarze
Witam.
Moja propozycja rozwiązania dwuchodówki „treningowej”:
skoczek z d4 na e6.
Pozdrawiam
Piotr
Tak na szybkości spróbuję rozwiązać pierwsze zadanie:
Se6
Nie wiem czy dobrze.
Dwuchodówka treningowa:
1. Sd4-f5
Grozi i po większości odpowiedzi następuje:
2. Wd5-d4X
Pozostałe możliwości:
1… Wc2-d2, 2. Sd1-c3X
1… Wc6-d6 lub 1… Wc6-c7, 2. Sf5-d6X
1… Gh4:g5, 2. Sf5-g3X
Może jakiś wariant przeoczyłem, ale wydaje mi się, że to wszystkie.
Pozdrawiam
AB
Do Piotra44 i Janosława:
Na 1. Sd4-e6 gram 1… Wc2-d2
i według mnie mata nie ma.
Ale blisko…
Pozdrawiam
AB.
Stawiam na Sd4-b3.
Po Sd4-e6, czarne bronią Wc2-d2.
Pozdrawiam.
Witam.
Do Andrzeja69: niestety przeoczyłem ruch wieżą z c2 na d2 (a to „blisko” to trochę jak w TOTO-LOTKU – najczęściej wylosowane liczby są blisko tych skreślonych :)).
Pozdrawiam
Piotr
> Stawiam na Sd4-b3.
Czarny pionek c4 może tego skoczka zbić.
Do Eljota:
Po 1. Sd4-b3 następuje 1… Gh4:g5
Pozdrawiam
AB
Przepraszam z góry, że nie na temat, ale jako że pisuje tutaj sporo matematyków, a przynajmniej wypowiedzi niektórych na to wskazują, w związku z tym mam następujące dwa pytania-prośby:
1. Da się jakąś niezbyt trudną metodą wyznaczyć np. cos(36°)?
Albo jakiegoś kąta „w miarę proporcjonalnego” do podanego, np. 18, 54, 72. Może być też sinus.
Nie chodzi mi o wartości, które znam. Proszę o informację, jak to policzyć.
2. Prosiłbym też o rozwiązanie, w sposób w miarę zrozumiały, równania:
cos(4x)=-cos(6x)
Z góry dzięki za wsparcie w temacie poniekąd łamiblogowym.
janoslaw
1) 1. Gd1-f3
2) 1. Sf5-d4
3) 1. Hd1-d3+
Czy z tym trzecim zadaniem jest wszystko w porządku?
Wydaje mi się, że po podanym ruchu nie ma obrony przed matem w następnym, a trochę to nie pasuje do reguł rządzących szachowymi problemami.
Szach w pierwszym posunięciu i do tego jeszcze dosyć „mało finezyjny” 😉 ???
Pozdrawiam
AB
Andrzej69:
W takiej formie zadanie otrzymałem od Piotra Murdzi, ale obawiam się, że ma Pan rację. Trochę w tym mojej winy, że wcześniej nie sprawdziłem rozwiązania. Poprawianie teraz nie ma sensu o tyle, że po nim wszystko będzie jasne jak na dłoni. Mimo to niebawem zmienię diagram na właściwy.
Przy okazji gratuluję wyniku.
mp
Ufff… 🙂
Teraz, na spokojnie 😉 , napiszę trochę więcej.
1)
1. Gd1-f3
Grozi i po większości odpowiedzi następuje:
2. Wd5-d2X
Pozostałe warianty:
1… Hg3:f3, 2. Gf6-h4X
1… Wh2-dow.2, Gf6-g5X
2)
1. Sf5-d4
Grozi i po większości odpowiedzi następuje:
2. Sd4-b3X
Pozostałe warianty:
1… Hf2:d4, 2. Hg4:c8X
1… Sa3-dow., 2. Wb6-b5X
1… a5-a4, 2. Gd2-b4X
3) (w wersji właściwej z hetmanem na h1)
1. Hh1-d1
Bezpośredniej groźby nie ma, ale stawia czarne w tzw. zugzwangu (dowolny ich ruch prowadzi do pogorszenia pozycji).
I tak jeśli:
1… Wc5-c-dow. lub 1… Wc5-d5, 2. Hd1-d5X
1… Wc5-e5, 2. f4:e5X
1… Wd7-dow., 2. Sc6-e7X
1… Gh3-dow., 2. Hd1:g4X
1… Sb5-dow., 2. Sc6-d4X
1… Sd6-dow., 2. Hd1:d7X
1… g4-g3, 2. Hd1-h5X
1… h6-h5, 2. Wg8-g5X
Mam nadzieję, że w podanych rozwiązaniach nie przeoczyłem żadnej możliwości.
Natomiast nawiązując do Pańskiej, Panie Marku, odpowiedzi na mój komentarz dotyczący pierwotnej wersji trzeciego zadania, to wydaje mi się, że nie trzeba było pisać, że po poprawieniu „wszystko będzie jasne jak na dłoni”, gdyż wg mnie wcale nie jest takie oczywiste, że diagram przedstawiał pozycję po pierwszym ruchu białych. Generalnie to zadanie nie jest proste (jak na dwuchodówkę) – powiedziałbym nawet, że zdecydowanie trudniejsze od dwóch wcześniejszych. Ja osobiście po obejrzeniu właściwej pozycji początkowo nie widziałem w jaki sposób wcześniejszy diagram miałby ułatwić rozwiązywanie. W końcu z tej pozycji mata również daje się w dwóch posunięciach (w jednym nie da rady), a więc razem z 1. Hh1-d1 byłyby trzy. Dopiero po dokładniejszej analizie spostrzegłem, że po pierwsze: czarne są w zugzwangu (gdyby one zaczynały, to po każdym ich posunięciu białe matują w jednym ruchu! Niektóre warianty są identyczne z podanymi powyżej, niektóre – po 1… Gh3-dow., 1… Sd6-dow. i 1… g4-g3 – całkiem inne, ale skuteczne), lecz po drugie: białe poniekąd też 😉 – brakuje im całkowicie neutralnego ruchu! Dopiero wtedy skojarzyłem informację o potencjalnym ułatwieniu i oczywiście zacząłem sprawdzanie od posunięcia 1. Hh1-d1. Myślę, że gdybym jej nie miał (mam na myśli, nie tyle pierwotny diagram, co wypowiedź, że ułatwia on sprawę) zadanie stawiałoby opór trochę dłużej, bo, jeszcze raz podkreślę, ten ruch wcale nie był oczywisty (w przeciwieństwie do większości spraw dla odchodzącej ekipy rządzącej 😉 ).
Pozdrawiam
AB
PS: Dziękuję za gratulacje, ciekaw jestem, jak inni?
Do janoslawa:
cos 18 = cos(90-18) = sin 72
cos 18 = 2sin36cos36
cos 18 = 4sin18cos18cos36
4sin18cos36 = 1
4sin18(cos18 ^ 2 – sin18 ^ 2) = 1
4sin18(1-2sin18 ^ 2) = 1
8 sin18^3 – 4sin18 + 1 = 0
Jednym pierwiastkiem jest 1/2 – reszte sie daje policzyc.
A to drugie moze pomysle jak bede mial jasniejszy umysl 😉
Pozdro,
MK
Do Janoslawa:
cos(4x)=-cos(6x)
cos(6x)+cos(4x)=0 dalej ze wzoru na sumę cosinusów
2cos(5x)cosx=0 stąd
cos(5x)=0 lub cosx=0
5x=1/2pi+kpi lub x=1/2pi+kpi
x=1/10pi+1/5kpi lub x=1/2pi+kpi
Dzięki za wsio:
Ale w jednym zadaniu wychodzi na to, że sinusem 18 może być 1/2…
Tak chyba będzie lepiej:
cos54 = sin36
cos54 = 2sin18*cos18
cos(36+18) = 2sin18*cos18
cos36*cos18 – sin36*cos18 = 2sin18*cos18
cos36*cos18 – 2(sin18)^2*cos18 = 2sin18*cos18
cos36 – 2(sin18)^2 = 2sin18
2(cos18)^2 – 1 – 2(sin18)^2 = 2sin18
1 – 4(sin18)^2 = 2sin18
4t^2 + 2t – 1 = 0
I wtedy są dwa rozwiązania, w tym jedno ujemne, które się odrzuca.
Ale dzięki za podsunięcie pomysłu.
Do jawy:
Żeby przekształcić to do:
2cos(5x)cosx=0
to mi się udało wymyślić, ale za nic nie wpadłem, żeby to oba składniki przyrównać do zera
Też wielkie spasiba.
Do Piotra44:
Porównanie z Toto-Lotkiem, jako żart – zabawne 🙂 , ale nie o takie „blisko” (w sensie pole sąsiednie) mi chodziło. Uporządkowanie numerów w „Totku” nie ma przecież żadnego znaczenia (10 jest tak samo blisko 11 jak i np. 41), a tu sytuacja jest zdecydowanie inna:
Po pierwsze: ruch właściwą figurą.
Po drugie: prawidłowa groźba (2. Wd5-d4X).
I po trzecie: są odpowiedzi na dwie obrony czarnych, tzn. 1… Wc6-d6 i 1… Gh4:g5.
Niestety zabrakło uwzględnienia trzeciej.
Ale idea dobra, jedynie wymagająca dopracowania.
Miałem nadzieję, że moje rozwiązanie nie ukaże się od razu i to „blisko” miało być małą sugestią, że kierunek poszukiwań jest dobry, tylko brakuje kropki nad „i”.
Pozdrawiam
AB
Do Janoslawa:
Cosinus 36° można też obliczyć np. tak:
Opieram się na wzorze na sin5x (nie będę go tu wyprowadzać, bo jest to dość proste – korzystamy z sinusa i cosinusa sumy)
sin5x = sinx*(16(cosx)^4-12(cosx)^2+1),
a za x przyjmujemy 36°.
Ponieważ sin(5*36°) = sin180° = 0
oraz sin36° jest różne od 0
więc 16(cos36°)^4-12(cos36°)^2+1 = 0.
Z tego otrzymujemy:
(cos36°)^2 = (3 +/- sqrt5)/8 =
= ( (sqrt5 +/- 1)/4 )^2
a więc, odrzucając wyniki ujemne, mamy:
cos36° = (sqrt5 +/- 1)/4.
Dlaczego rozwiązania są dwa?
Ano dlatego, że przy okazji wyliczyliśmy cos72°.
W końcu sin(5*72°) = sin360° = 0 również.
Które jest które?
Ponieważ cosinus jest funkcją malejącą (w pierwszej ćwiartce) więc mniejszemu argumentowi odpowiada większa wartość.
A zatem: cos36° = (sqrt5 + 1)/4.
Pozdrawiam
AB
Oglądałam przed laty program o 10-latku (Polaku), którego ojciec nauczył
grać w szachy. Chłopak z ojcem wygrywał, potem grali tak, że chłopiec
siedział tyłem do szachownicy (ojciec przestawiał figury na jego
polecenie i informował go, jak przestawił swoje). Takie partie chłopiec
też wygrywał. Wygrywał też w symultankach. Kto to może być, czy
to ktoś obecnie znany? Niestety, nie pamiętam nazwiska. Wiek – obecnie
może około 25 lat, tak mi się wydaje.
Witam.
Rozwiązania dwuchodówek (choć zdaję sobie sprawę, że już dawno „po zawodach” 😉 – ale dopiero teraz mogłem się zabrać za rozwiązywanie zadań):
1. Gd1:f3;
2. Hg4:e4 [lub Hg4:f4 – wygląda na to (o ile czegoś nie przeoczyłem), że ta dwuchodówka ma dwa rozwiązania];
3. Hh1:d1.
Pozdrawiam
Piotr
No, Andrzeju, piękne rozumowanie, tylko czy potrafisz powiedzieć skąd wiesz, że
sqrt[(3 +/- sqrt5)/8] to (sqrt5 +/- 1)/4 )
Bo chciałbym w podobny sposób uprościć podobne wyrażenia, żeby uzyskać sinusy 36 i 72:
Odpowiednio
sin36=sqrt[(5-sqrt5)/8]
sin72=sqrt[(5+sqrt5/8]
Bo sam widzisz, że pierwiastek pod pierwiastkiem to tak głupio wygląda.
Próbuję, próbuję, ale nie bardzo mi wychodzi
Do Andrzeja69:
Zrozumiałem sens użycia przez Ciebie słówka „blisko”. Tyle tylko, że równoczesne ukazanie się Twojego komentarza z prawidłowym rozwiązaniem, sprowadziło pojęcie „bliskości” raczej do znaczenia „totolotkowego” :).
Mimo wszystko dzięki wielkie za próbę pomocy.
Pozdrawiam
Piotr
Do Janosława:
Dzięki za uznanie.
Masz jak najbardziej rację, że pierwiastek pod pierwiastkiem wygląda mało sympatycznie.
Ja to uprościłem w ten sposób (korzystając ze wzoru na kwadrat sumy lub różnicy, tylko od tyłu):
sqrt[(3 + sqrt5)/8] =
= sqrt[(6 + 2sqrt5)/16] =
= sqrt[(5 + 2sqrt5 +1)/16] =
= sqrt[((sqrt5)^2 + 2sqrt5 +1)/16] =
= sqrt[(sqrt5 + 1)^2 / 4^2] =
= (sqrt5 + 1)/4
Ta metoda nie zawsze działa, no ale jak się nie udaje, to najprawdopodobniej oznacza, że niestety tak musi pozostać. W przypadkach, o które się pytasz, nie ma problemu, ale wyniku celowo Ci nie podam, aby nie zabierać „przyjemności” 😉 własnoręcznego przekształcenia (sposób już znasz).
Pozdrawiam
AB
PS: Zastawiałem się też nad geometrycznym wyznaczeniem cosinusa 36°, tzn. jako stosunku długości odcinków łączących środek pięciokąta foremnego ze środkiem jego boku oraz z jego wierzchołkiem. Oczywiście, żeby miało to sens, nie wolno przy tym używać trygonometrii, o którą co krok aż się prosi. Tak że na razie dałem sobie spokój. Spróbuję jeszcze za jakiś czas.
Do Andrzeja69:
Wiedziałem, że działałeś z kwadratu sumy, ale przypadki sin18 i sin54 były w omawianej sytuacji chyba najprostsze, jakie się mogły zdarzyć(1*pierwiastek +/- 1)
Jednak nie udało mi się zgadnąć, ani wywnioskować tych kwadratów dla sin36 ani sin72.
Czy mógłbym prosić o podanie tych wyników, bo „przyjemność” rozwiązywania zmieniła się w walkę z samym sobą. :/
Do Janoslawa:
Muszę Cię niestety przeprosić za podanie błędnej informacji (i wrobienie w upraszczanie), ale faktycznie przypadków, o które się pytałeś chyba lepiej przedstawić się nie da (co najwyżej jako: sqrt(10 +/- sqrt5)/4, ale to żadne osiągnięcie). Szczerze mówiąc zastanawiałem się nad nimi bardzo szybko i 5+4 dało mi w wyniku… 10 :-(. Myślami byłem chyba wtedy przy szachach i zastanawiałem się nad brakiem zainteresowania dwuchodówkami, ale ten temat poruszę już w innym komentarzu.
Także jeszcze raz przepraszam.
Pozdrawiam
AB
Do Piotra44:
1.Hg4-e4 i 1.Hg4-f4 nie są rozwiązaniami drugiej dwuchodówki ze względu na 1…Hf2-g1.
To zadanie nie polega na zugzwangu, chociaż na takie może wyglądać, ale to chyba sytuacja niezamierzona, a wynikająca jedynie z ekonomii przedstawienia problemu. Tutaj trzeba podjąć trochę bardziej aktywne działania 😉 .
Prawidłowe rozwiązanie już pewnie widziałeś, a trochę więcej na ten temat spróbuję napisać w komentarzu do następnego odcinka.
I jeszcze drobna uwaga na temat notacji szachowej:
Nie traktuj tego jako wytykanie (wiem, że nie grasz w szachy), a jedynie jako sugestię na przyszłość.
Jeśli zapisujesz ruch bez bicia, jako separatora między polem startowym a docelowym używaj myślnika. Dwukropek oznacza bicie (obecnie chyba częściej używa się „x”, ale wg mnie ten sposób jest mniej czytelny).
Pozdrawiam
AB
Witam.
Do Andrzeja69: szczerze gratuluję wyniku.
Dziękuję za uwagi krytyczne. W drugim zadaniu sam znalazłem błąd (w gruncie rzeczy podane przeze mnie „rozwiązanie” to takie bardziej bez sensu jest 😉 – ale, jak to mówią, „nie myli sie tylko ten, kto nic nie robi”). Jeśli chodzi o notację szachową, to szczerze powiem, że nie wiem dlaczego wpisałem „:” zamiast „-” (to trochę tak jakby ręka zrobiła coś innego, niż chce głowa 🙂 – taka jakby „palcówka”).
Też byłem bardzo zaskoczony faktem, że do rozwiązywania zadań w zasadzie nikt się nie zabrał. Przecież to tylko rozrywka (bardzo pasjonująca – przynajmniej dla mnie), a nie jakieś śmiertelnie poważne zawody. I choć Twoje wyniki nie były dla mnie zaskoczeniem (i to nie jest jakieś „kadzenie” :), tylko może przeczucie raczej), to myślałem, że jeszcze kilka osób spróbuje rozwiązać te dwuchodówki (niekoniecznie najszybciej). To, że tak się nie stało jest być może wynikiem braku cierpliwości, a może faktycznie „wąskiej specjalizacji” (jak sugeruje Pan Marek w następnym wpisie). Trochę szkoda, a i smutne jest to, że wszechogarniająca specjalizacja może dotknąć także rozrywek umysłowych (przecież każda „wąska specjalizacja” w gruncie rzeczy ogranicza człowieka).
Pozdrawiam i jeszcze raz gratuluję
Piotr