Sudoku z magią

25 października 2007
Marek Penszko

Warunkiem koniecznym tego, aby zwykłe sudoku miało dokładnie jedno rozwiązanie, jest co najmniej siedemnaście liczb ujawnionych na początku w diagramie, w tym przynajmniej osiem różnych. Jeśli jednak zadanie będzie „niezwykłe”, czyli uzupełnione dodatkową regułą, wówczas liczby w warunku koniecznym mogą być mniejsze. Na przykład, żądając, aby na przekątnych także znalazło się dziewięć różnych cyfr (sudoku X), możemy zmniejszyć ogólne minimum z siedemnastu do tuzina.

Jeżeli dodatkowa reguła nie wymaga umieszczania dodatkowych oznaczeń w diagramie albo przynajmniej oznaczenia te nie są konieczne (np. w sudoku X można pominąć zaznaczenie przekątnych linią lub kolorem, wystarczy o tym napisać), wówczas mamy do czynienia z sudoku, dla którego zaproponowałem określenie „parzące”. Można się na takiej odmianie sparzyć, jeśli nie podejrzewa się obecności dodatkowej reguły, bo skoro wygląd diagramu na to nie wskazuje, to z marszu próbuje się je rozwiązywać jak zwykłe sudoku, bez zerknięcia na instrukcję. Sparzenie się polega oczywiście na tym, że rozwiązać zadania nie sposób, a ściślej: ma ono tak wiele rozwiązań, że zabawa traci sens. Przykładem może być poniższy diagram – nie uda się w nim jednoznacznie ustalić położenia żadnej cyfry, jeżeli przez nieuwagę (przymało cyfr w diagramie) pominie się informację, że jest to sudoku X.

sudm_1.JPG 

W komentarzach Michał zaproponował ułożenie wariantu sudoku bez dodatkowych oznaczeń w diagramie lub obok niego, z najmniejszą możliwą liczbą różnych cyfr ujawnionych na początku. Uściśliłem, by ograniczyć się do wariantów parzących i niniejszym proponuję pobicie poniższego rekordu – pięć ujawnionych cyfr, w tym trzy różne.

sudm_2.jpg 

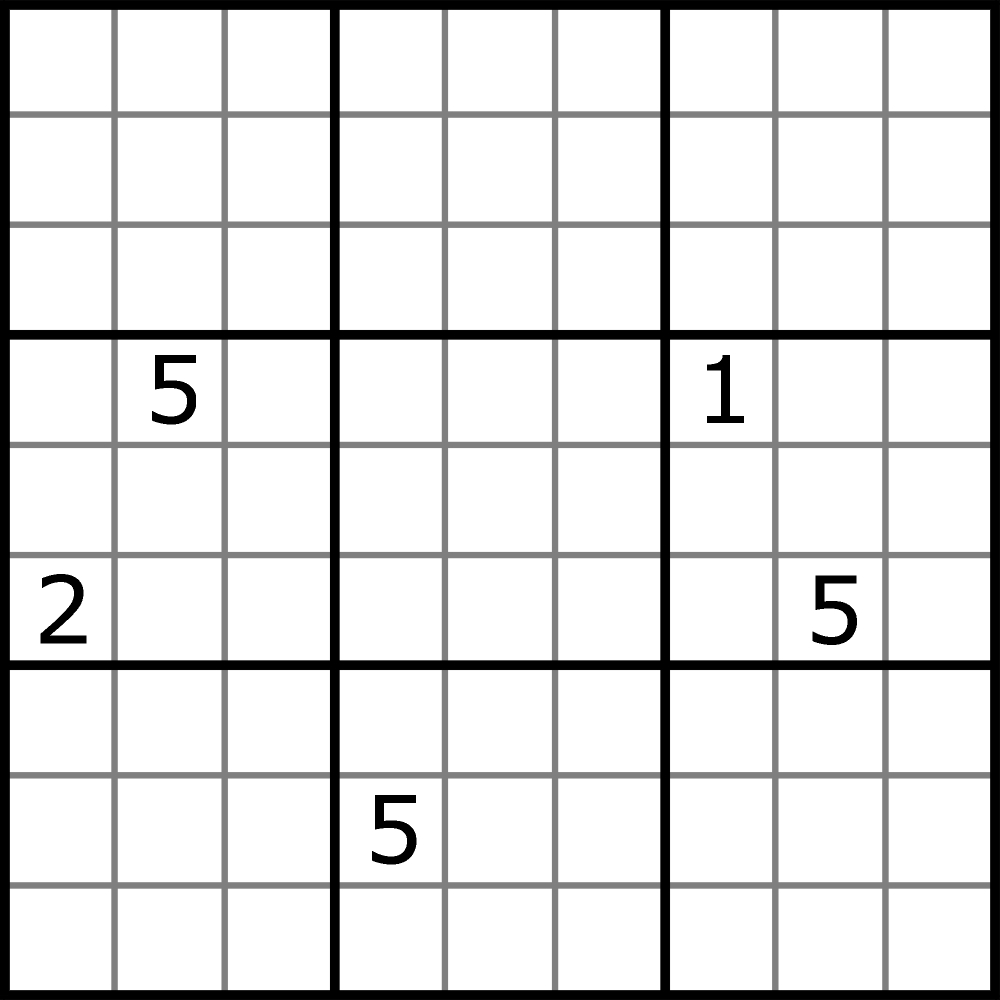
Prawdę mówiąc, określenie „parzące” nie bardzo do tego zadania pasuje, bo pozorny niedobór cyfr jest tak znaczny, że natychmiast sugeruje, iż coś jest nie tak i zmusza do przeczytania instrukcji – zawarta w niej dodatkowa reguła brzmi następująco: w rozwiązaniu powinno pojawić się pięć kwadratów magicznych 3×3. Innymi słowy, niektóre kwadraty złożone z 9 kratek, ale – co nietrudno zauważyć – nie pokrywające się z wyznaczonymi przez grubsze linie sektorami 3×3, powinny być kwadratami magicznymi: w każdym suma trzech cyfr w wierszach, kolumnach i na obu przekątnych powinna być taka sama.

Mając solidne podstawy, czyli po prostu wiedząc, jak wygląda kwadrat magiczny 3×3, zadanie rozwiązuje się prawie jak po sznurku, bez większych przeszkód, a finał jest jednoznaczny.
Niewykluczone, że idąc magicznym tropem i ewentualnie dodając jeszcze jakiś warunek, ale oczywiście bez umieszczania oznaczeń na rysunku, można by z liczbą danych wstępnych zejść poniżej pięciu.

Przy okazji informacja dla wszystkich, którzy chcieliby sprawdzić, jakie mieliby szanse w Mistrzostwach USA w sudoku, które odbyły się w Filadelfii 19-20 października. Na stronie mistrzostw znajdują się trzy zadania finałowe w trzech kategoriach – dla początkujących, średniaków i zaawansowanych. Przy odpowiedziach podane są czasy, które zapewniły najlepszym zwycięstwo i niemałe nagrody ufundowane przez wydawcę dziennika Philadelphia Inquirer. Niespodzianki nie było – mistrzem nad mistrzami okazał się aktualny mistrz świata Thomas Snyder.
„Taka kasa przeszła mi koło nosa” – stwierdził półżartem nasz mistrz Jan Mrozowski, który wirtualnie, czyli w bezstresowych warunkach domowych okazał się lepszy od Thomasa Snydera o 20 sekund.