Sudoku roku
16 WPC, czyli Łamigłówkowe Mistrzostwa Świata są odcięte od świata. Przynajmniej dotychczas i oficjalnie, bo organizatorzy nie tylko nie zamieszczają na stronie interentowej informacji bieżących, ale nie podali nawet listy uczestników. W internecie można jednak obejrzeć 2-minutowe wideo z pierwszego dnia zmagań. Wyczytałem też w prasie brazylijskiej, że startują drużyny z 26 krajów, a z kongresu WPF (World Puzzle Federation) dotarła nieco zaskakująca wiadomość – w 2009 roku Sudokowe Mistrzostwa Świata będą prawie w Polsce, bo jak się dobrze rozpędzę to w jeden dzień rowerem do słowackiej Żyliny zajadę. Turcy znowu się nie załapali – wygrała koncepcja, aby nie tylko kraj, ale i kontynent, jeśli to możliwe, co roku był inny. W tej sytuacji zmalały szanse Polski na rok 2010. Zanim pojawią się – zapewne jeszcze dziś – ostateczne wyniki 16 WPC, pozostańmy przy sudoku.
Na jednym z forów ogłoszono wyniki plebiscytu na sudoku roku, czyli najciekawszą i najatrakcyjniejszą odmianę tej łamigłówki. Działo się to minionej zimy i dotyczyło roku 2006, gdy moda na sudoku jeszcze trwała, choć jej apogeum już minęło. Dziś taki plebiscyt nie miałby sensu. Wprawdzie nowych odmian nie brakuje, jednak nie mają one dostatecznej siły przebicia, zna je wąskie grono zapaleńców i na ogół są raczej dziwaczne niż ciekawe.
Najwięcej głosów zebrał wówczas killer, a szósty był mój faworyt – odmiana, która najbardziej dała się we znaki finalistom 1 Mistrzostw Świata, czyli sudoku toroidalne. Rozwiązał je tylko jeden z czwórki najlepszych (Thomas Snyder), pozostali nie tylko nie dali rady, ale w ciągu 15 minut każdy wpisał do diagramu zaledwie jedną cyfrę! W tym cały urok tej odmiany – dodanie jednego prostego warunku mocno „zakręca” zabawę. Warunek dodawany jest do sudoku nieregularnego, zwanego także jigsaw, które można by nawet uznać za klasyczne, bo pojawiało się w prasie na całym świecie na długo przed sudokową epidemią.
Po raz pierwszy 81 kratek trafiło na torus 2,5 roku temu w Łamigłówkowych Mistrzostwach USA i wyglądało jak na poniższym diagramie.
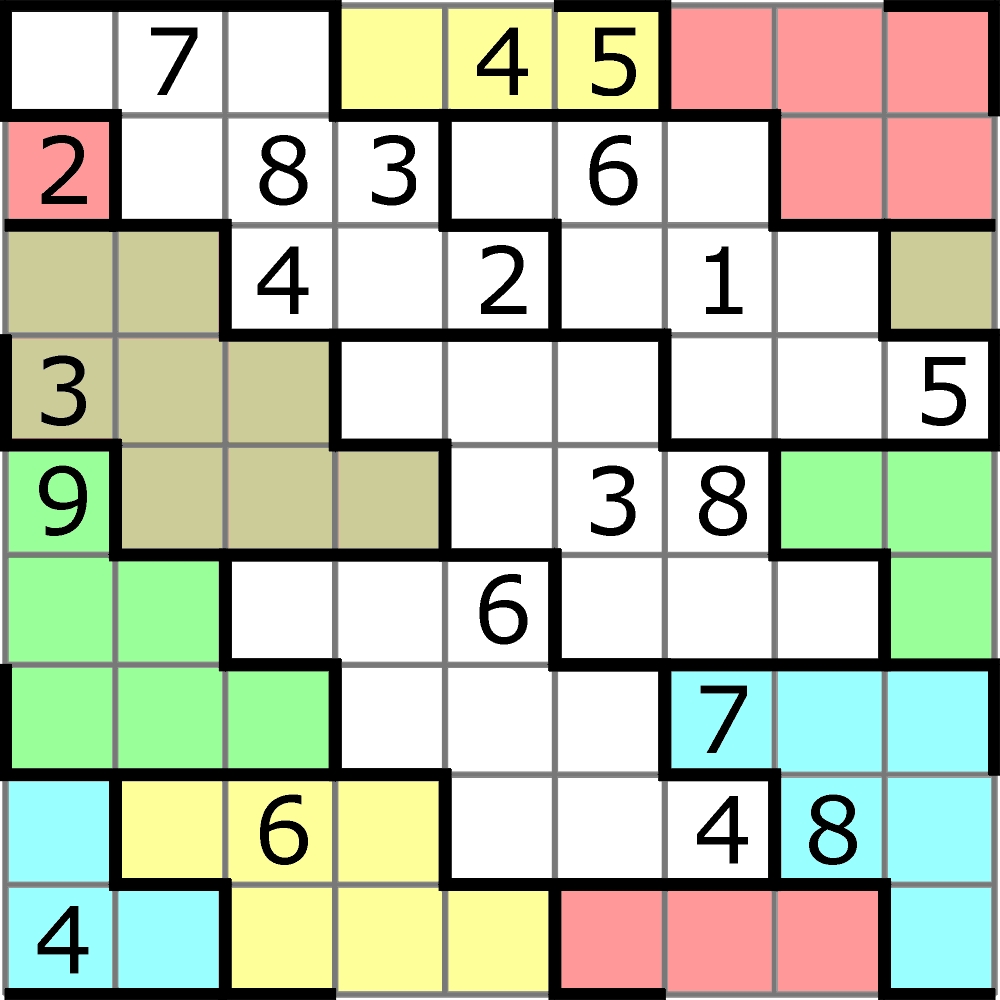
Podstawowe reguły są niezmienne: dziewięć różnych cyfr w każdym wierszu, kolumnie i obszarze otoczonym grubą linią. Cały smaczek w tym, że diagram jest jakby rozciętym i rozpłaszczonym walcem pionowym i poziomym równocześnie. Inaczej mówiąc, niektóre obszary (gwoli jasności oznaczone takim samym kolorem) są pokawałkowane przynajmniej na dwie części. Fragment każdego z nich, „urywający się” na jednym brzegu, ma dalszy ciąg na przeciwległym. Nic dziwnego, że dla Thomasa Snydera zatknięcie się z tym zadaniem zaprocentowało handicapem na Mistrzostwach Świata; pozostałym finalistom zabrakło czasu nawet na oswojenie się z nową sytuacją, nie mówiąc o skutecznym główkowaniu.
Odtąd sudoku toroidalne gości na turniejach i w programach mistrzostw, ale niezbyt często, bo nie jest łatwe do ułożenia – zakładając, że powinno być także zadaniem ambitnym, czyli z minimalną liczbą ujawnionych cyfr. Koneserom interesujących odmian i zwolennikom mierzenia sił na zamiary proponuję uporanie się z poniższym toroidalnym orzechem bardzo twardym do zgryzienia.
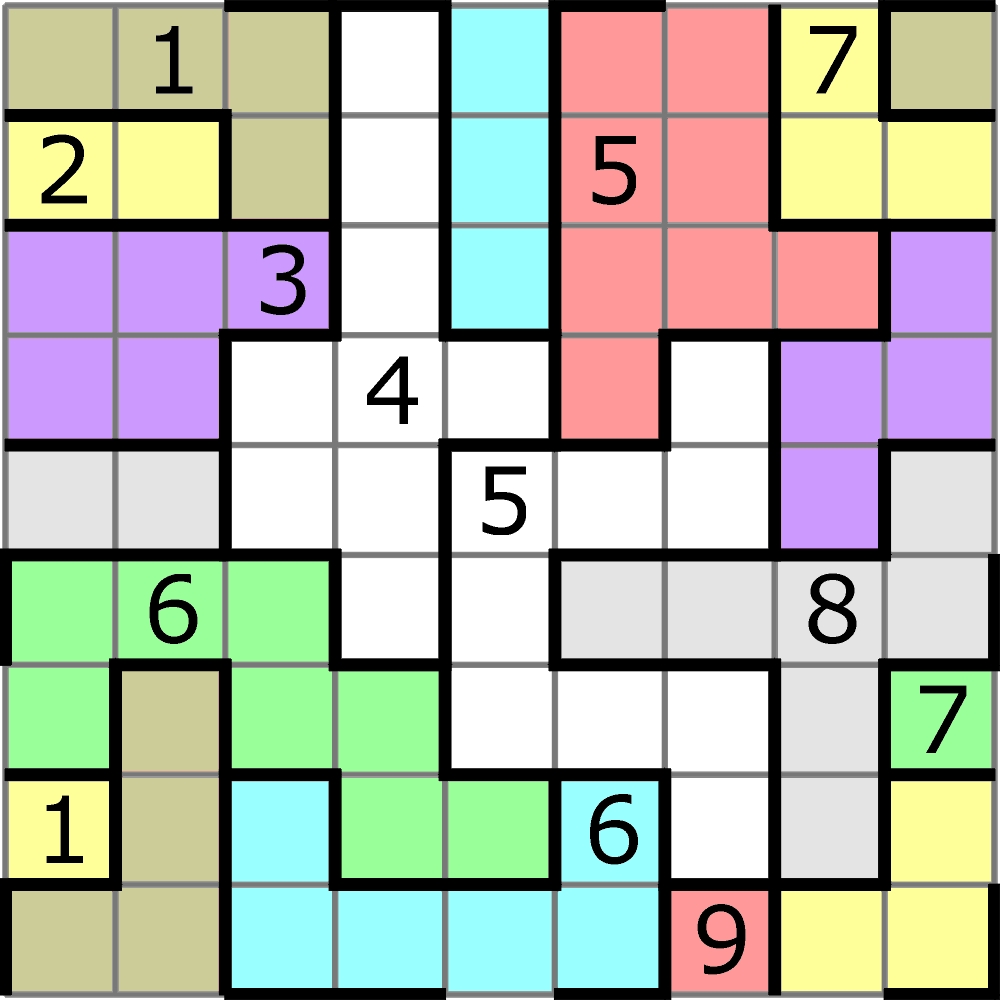

Komentarze
Witam
Rozwiązywanie drugiego sudoku toroidalnego jest raczej dla pasjonatów tego rodzaju zabawy albo dla masochistów, którzy powinni być usatysfakcjonowani ciągłymi przeszkodami wiodącymi do celu, bo zadanie jest z tych, gdzie ciągle jest pod górkę.
Dla Thomasa Snydera 5 za rozwiązanie, a dla pozostałej trójki finalistów pozostało patrzenie (prawdopodobnie) na 5.
Pozdrawiam
rozwiązanie I zadania:
679245318
218376954
764528139
381697245
925413867
837964521
542831796
196752483
453189672
Rozwiązanie II zadania:
916238475
297685143
483597621
759413862
678351294
361742589
524869317
145926738
832174956
Pozdrawiam
A mi się takie sudoku niesamowicie podoba, bo nietypowosc zasad powoduje, ze wiekszosc „typowych” technik sudoku nie dziala i trzeba wymyslac wlasne metody 🙂
Szkoda ze niestety torus nie jest plaski – wiec nie da sie tego kwadracika ladnie skleic… Hmm, a moze uzyc jakiegos programu do grafiki 3-D?
Aha i rozwiazania:
Torus I
679 245 318
218 378 954
764 528 139
381 697 245
925 413 867
837 964 521
542 831 796
196 752 483
453 189 672
Torus II
916 238 475
297 685 143
483 597 621
759 413 862
678 351 294
361 742 589
524 869 317
145 926 738
832 174 956
Odpowiedzi:
679245318
218376954
764528139
381697245
925413867
837964521
542831796
196752483
453189672
oraz:
916238475
297685143
483597621
759413862
678351294
361742589
524869317
145926738
832174956
Witam.
Rozwiązania SUDOKU TOROIDALNYCH (rzędami od góry):
1. z Mistrzostw USA:
6 7 9 2 4 5 3 1 8
2 1 8 3 7 6 9 5 4
7 6 4 5 2 8 1 3 9
3 8 1 6 9 7 2 4 5
9 2 5 4 1 3 8 6 7
8 3 7 9 6 4 5 2 1
5 4 2 8 3 1 7 9 6
1 9 6 7 5 2 4 8 3
4 5 3 1 8 9 6 7 2
2. „twardy orzech”:
9 1 6 2 3 8 4 7 5
2 9 7 6 8 5 1 4 3
4 8 3 5 9 7 6 2 1
7 5 9 4 1 3 8 6 2
6 7 8 3 5 1 2 9 4
3 6 1 7 4 2 5 8 9
5 2 4 8 6 9 3 1 7
1 4 5 9 2 6 7 3 8
8 3 2 1 7 4 9 5 6
Pozdrawiam
Piotr
Moim zdaniem takie sudoku jest bardzo ciekawe i mniej w nim szablonowego „dziergania”, a za to zdecydowanie więcej używa się wyobraźni (choć bynajmniej nie przestrzennej 😉 ). Spostrzegawczość również należy ukierunkować bardziej na kształty poszczególnych obszarów niż tylko na obecność konkretnych cyfr.
Pierwsze zadanie jest bardzo łatwe i można je rozwiązać niejako z marszu. Drugie jest zdecydowanie trudniejsze, choć również do zrobienia, zresztą tym bardziej, iż okazuje się być tak ułożone, że można je rozwiązywać jak po sznurku (trzeba tylko ten sznurek odnaleźć 😉 ). To przypuszczam konsekwencja bardzo małej ilości znanych od początku cyfr: raptem tylko 13! Z tego co pamiętam to do tej pory nikt nie ułożył mającego jedno rozwiązanie klasycznego sudoku, które by miało ich mniej niż 17.
Dla tych, którzy nie mieli wystarczająco cierpliwości, aby się przez nie przegryzać, podaję dwie wskazówki:
Pierwsza: Proponuję przed wydrukowaniem diagramu ze strony wkleić go do jakiegoś programu graficznego, a następnie skopiować 8 razy i ułożyć obok siebie tworząc kwadrat 3×3. Wówczas poszczególne obszary będą widoczne w całości i nie trzeba będzie „skakać” wzrokiem z jednego końca na drugi. A jeśli ktoś przenosi ręcznie to po prostu dorysować z każdej strony po dwa lub trzy rzędy (kolumny) pól.
Druga to „sznurek”. Wg mnie najlepsza kolejność rozwiązywania jest następująca: 5, 6, 7, 1, 9, 2, 3, 8, 4. Tzn. najpierw znajdujemy wszystkie piątki. Gdy już mamy ostatnią, to dalej wszystkie szóstki, potem siódemki (tu jedyny wyjątek: na tym etapie nie uda się wszystkich – położenie dwóch ostatnich ustalamy na końcu) itd… W przypadku ostatnich cyfr oczywiście jest duża dowolność, na początku raczej o nią dość trudno.
A oto kompletne rozwiązania obu zadań:
6 7 9 2 4 5 3 1 8
2 1 8 3 7 6 9 5 4
7 6 4 5 2 8 1 3 9
3 8 1 6 9 7 2 4 5
9 2 5 4 1 3 8 6 7
8 3 7 9 6 4 5 2 1
5 4 2 8 3 1 7 9 6
1 9 6 7 5 2 4 8 3
4 5 3 1 8 9 6 7 2
9 1 6 2 3 8 4 7 5
2 9 7 6 8 5 1 4 3
4 8 3 5 9 7 6 2 1
7 5 9 4 1 3 8 6 2
6 7 8 3 5 1 2 9 4
3 6 1 7 4 2 5 8 9
5 2 4 8 6 9 3 1 7
1 4 5 9 2 6 7 3 8
8 3 2 1 7 4 9 5 6
Pozdrawiam
AB
Pierwsze sudoku toroidalne jest łatwe, ale drugie rozwiązuje się znacznie przyjemniej i bez wielkich oporów, choć oczywiście nielekko. Należy ujawniać etapami poszczególne cyfry, tzn. najpierw wszystkie cyfry x, potem y itd. (na początku oczywiście te, które są już dwie w diagramie), choć nie zawsze wszystkie udaje się ujawnić.
Konkretnie: najwygodniej zacząć od wpisania małych cyferek x w pola, gdzie mogą się znajdować i analizować układ wszystkich tych możliwości – zwykle analiza jest mocno logiczna i prowadzi do eliminowania i pojawiania się jednoznaczności.
Spora satysfakcja.
Polecam (jako antidotum dla umęczonych kampanią wyborczą) i pozdrawiam.
c
Witam.
Maleńka uwaga do komentarza Andrzeja69: „magiczne 17” jako minimalna ilość cyfr wpisanych początkowo w diagram, dotyczy właściwie tylko klasycznego sudoku. W przypadku wszelkich odmian (np. mozaika, diagonalne, inne dodatkowe warunki) ilość ta jest inna (więcej na ten temat można przeczytać choćby w „PUZELANDZIE”, w październikowym numerze „Wiedzy i Życia”).
Pozdrawiam
Piotr
Do Piotra44:
W moim wcześniejszym komentarzu, powołując się na minimalną 17-stkę, napisałem, że chodzi o sudoku klasyczne. Przyjąłem właśnie je za punkt odniesienia, bo jest najprostsze i najbardziej znane. Jeśli weźmiemy pod uwagę mutacje, w których dochodzą DODATKOWE reguły (np. sudoku X) to z oczywistych powodów liczba początkowych cyfr może się zmniejszać. Natomiast tutaj dodatkowych zasad właściwie nie ma – są tylko dwie modyfikacje jednej ISTNIEJĄCEJ reguły: tzn. obszary nie muszą być kwadratowe i mogą być rozbite na części. A mimo to udało się dość znacznie obniżyć minimalną liczbę cyfr.
Pozdrawiam
AB
Też mi się udało 🙂
916238475
297685143
483597621
759413862
678351294
361742589
524869317
145926738
832174956
Andrzej69 zwrócił uwagę na małą liczbę podanych w zadaniu cyfr. Jest ich tylko 13. W Sudoku X, z październikowego numeru Wiedzy i Życia, jest podanych jeszcze mniej, bo 12 cyfr. Ciekawe jaka jest minimalna liczba cyfr dla Sudoku 9×9 z dodatkowymi warunkami. Na pewno co najmniej 8, ale czy komus udało się już skonstruować takie zadanie?
Michale, chyba warto by doprecyzować o jaki zakres warunków chodzi, bo jak się uprzeć, to warunki można tak sformułować, a na dokładkę w diagramie wyodrębnić dodatkowe obszary w taki sposób, że w ogóle nie będzie trzeba wpisywać żadnej cyfry.
Chodziło mi o to, żeby w diagramie było ujawnionych jak najmniej cyfr i żeby nie było żadnych cyfr obok diagramu (jak w „sudoku na boku”) ani żadnych liczb w diagramie (jak w killerze). Czy przy takich założeniach dałoby się zrobić zadanie bez żadnej ujawnionej cyfry?
Poprzednio napisałem, że takim absolutnym minimum powinno być 8. Ale może przy warunku „liczby nie po kolei” ten wynik dałoby się jeszcze poprawić.
Ciekawe. Pokombinuję i poszukam. Zachęcam do tego także innych główkołamaczy.
mp
Obawiam sie ze to nalezy jeszcze bardziej dopracowac. (uscislic) Zeby uniknac takich bzdur:
(Przyklad b. prosty uzywajacy kolorow)
Np. Rozwiaz sudoku wiedzac, ze kratki zamalowane:
– niebieskim maja 1
– zielonym maja 2
– czerwonym maja 3
itp… I rysujemy pusty diagram z masa kolorowych pol w srodku. (obejdzie sie bez zadnych liczb)
Do Esteona i Michała:
Pokolorowanie pól i napisanie, że kolor A oznacza cyfrę X, to w gruncie rzeczy wpisanie cyfr do pól, więc odpada. Ale zgadzam się, że zadanie warto by ściślej sformułować.
Moja propozycja:
Diagram 9×9 podzielony na 9 obszarów 9-polowych. Obowiązują zasady sudokowe plus dodatkowy warunek (warunki?) określający(e) zależności między cyframi. Wykluczone są dodatkowe oznaczenia w diagramie i warunki wprost przyporządkowujace cyfry polom.
Na stronie http://www.djape.net/sudoku/forum/viewtopic.php?t=938&postdays=0&postorder=asc&start=30 znalazłem sudoku z jednym rozwiązaniem, choć ujawnione są tylko 3 cyfry. Ale są trzy dodatkowe warunki:
– na głownych przekatnych są różne cyfry
– kolejne cyfry nie sąsiadują ze sobą
– „disjoint group” tzn. cyfry w tym samym położeniu w stosunku do kwadratów 3×3 są różne (np. w 9 środkach kwadratów są różne cyfry, w 9 lewych górnych rogach różne itd.)