Przez indukcję
Niezbyt często, ale w miarę regularnie docierają do mnie z Japonii pisma łamigłówkowe. Większość z nich w znacznej części wypełniona jest „sieczką”, od której i tak roi się w internecie, ale kilka ma ambicje nowatorskie. Pojawia się w nich sporo oryginalnych zadań i interesujących odmian tych dobrze znanych, np. sudoku. W jednym jest nawet odrębny obszerny dział zwany „kliniką”, w którym prezentowane są i analizowane nowe pomysły.
Niestety, język japoński nie jest moją mocną stroną, więc z reguły miewam do rozgryzienia dodatkowe łamigłówki. Każda z nich sprowadza się do rozszyfrowania na podstawie rysunku – zwykle przykładowego zadania z rozwiązaniem – zasad zabawy. To nietypowa i, szczerze mówiąc, jak dla mnie bardzo frapująca łamigłówka indukcyjna, a więc polegająca na wyciąganiu wniosków ogólnych z przesłanek, które są ich szczególnymi przypadkami. Może także Państwu przypadnie do gustu.
Poniżej zamieszczam dwa zestawy przesłanek. Każdy stanowi przykładową parę zadanie-rozwiązanie.
Pierwszy „przypadek kliniczny” jest prosty – reguły rozgryza się szybko i do cna.
Drugi to twardy orzech, z którym dotąd do końca sobie nie poradziłem, więc w Państwu cała nadzieja. Dodam, że jeden z kilku warunków, jakie powinno spełniać rozwiązanie, dotyczy kwadratów 2×2 kratki.
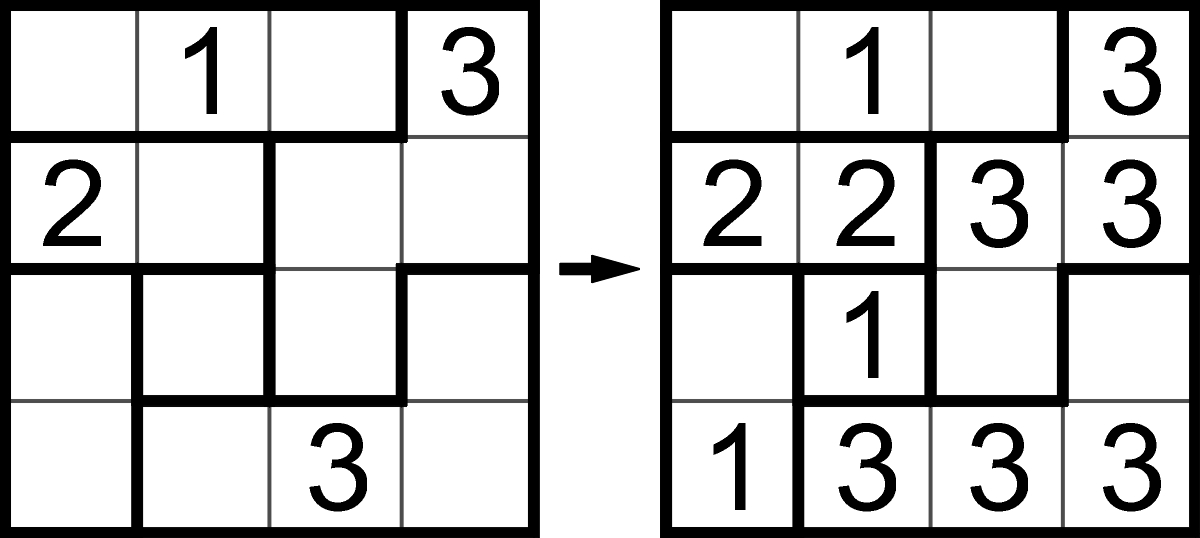
Na tych, którym uda się na podstawie powyższych przykładów, mimo skromnej porcji przesłanek w drugim przypadku, ustalić zasady obsługi obu łamigłówek, czekają dwa poniższe zadania – do rozwiązania, oczywiście zgodnie z rozszyfrowanymi zasadami.

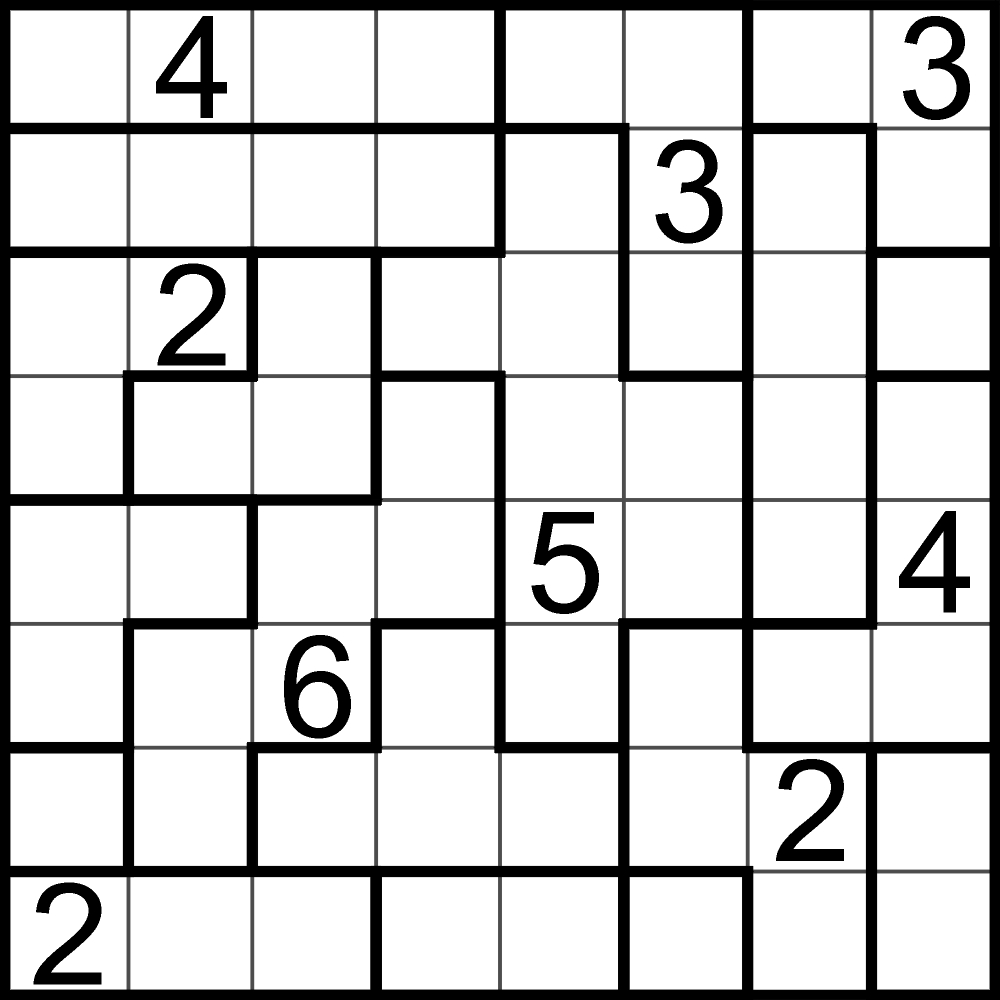
Życzę wytrwałości w dochodzeniu do całej prawdy (w przeciwieństwie do sytuacji życiowych, jest to możliwe) oraz przyjemnej zabawy.
PS Rezultat losowania nagrody (gra Scrabble) za rozwiązanie zadania pokerowego podam w następnym wpisie na początku przyszłego tygodnia.
Trzy osoby, które przesłały rozwiązanie tego zadania w ustalonym terminie na mój prywatny adres, proszę o bis w formie kometarza do poprzedniego wpisu.

Komentarze
Jezeli chodzi o pierwsza zagadke, to chyba jest jakas pomylka.
O ile dobrze zrozumialam zasady oczywiscie 🙂
W drugim rzedzie od gory sa dwie trojki w prawo i jedna 4 w lewo. Dla mnie to jest sprzeczne.
3 w trzeciej kolumnie sugeruje, ze sa zaznaczone 2, 1 i 4, 3 w pierwszej kolumnie sugeruje, ze trojki w 2-gim i 3-cim rzedzie nie sa zaznaczone. 4 w ostatnim rzedzie jednak wskazuje na zbyt mala ilosc zaznaczonych strzalek.
Czy to jest blad, czy zle zrozumialam zasady?
Czy ktoś z rozwiązujących ma inne zdanie na ten temat niż Agnieszka?
Do Agnieszki:
Według mnie to z zadaniem jest wszystko w porządku, być może powinnaś skorygować odgadnięte przez Ciebie zasady.
Nie wiem czy moja interpretacja reguł jest właściwa, ale przy ich zastosowaniu łamigłówkę udało się jednoznacznie rozwiązać.
Zasady i rozwiązanie wysyłam w osobnych komentarzach i pozostawiam decyzji Pana Marka, co ewentualnie ujawnić.
Pozdrawiam
AB
Według mnie zasady pierwszego zadania są następujące:
Strzałki podzieliłbym na „prawdomówne” 😉 („zakółkowane”) i „fałszywe”. Liczba w strzałce „prawdomównej” określa ile innych „prawdomównych” strzałek znajduje się w kierunku, który pokazuje. Liczba w strzałce „fałszywej” nie jest istotna (może również mówić prawdę, ale nie musi).
Założenia te pasują do przykładu, a zastosowane do zadania powodują, że wychodzi dokładnie jedno rozwiązanie, które przesyłam w następnym komentarzu.
Pozdrawiam
AB
Moje rozwiązanie pierwszego zadania („o” oznacza strzałkę „zakółkowaną”, „x” – nie):
o o x x o o
x o o o o o
x x o o o x
x o o o x o
x o o o o o
x o o o o x
Pozdrawiam
AB
Nie jest sprzeczne . Nie należy się sugerować wszystkimi liczbami , a tylko tymi , które są zakreślone . Dwie trójki w prawo i jedna czwórka w lewo nie stoją w sprzeczności , ponieważ po prostu nie można ich wszystkich trzech zakreślić w trakcie rozwiązywania . Ale pewności nie mam , bo zrozumienie zasad pierwszej zagadki potwierdzę dopiero gdy ją całą rozwiążę . Powodzenia
Witam
Do Agnieszki:
Pierwsze zadanie składa się z dwóch etapów:
– poznanie reguł
– rozwiązanie według reguł
Być może, że zasady, które obrałaś są błędne, bo zadanie posiada poprawne rozwiązanie.
Pozdrawiam
Zasadą w pierwszej zagadce (moim zdaniem) jest, że każda zaznaczona kółkiem strzałka wskazuje tyle zaznaczonych strzałek (w rzędzie albo w kolumnie, zgodnie ze zwrotem) jaka jest wartość liczby na tej strzałce.
W przykładzie: strzałka zaznaczona w pierwszym rzędzie (wierszu) wskazuje, że w tym wierszu, na prawo od niej, są jeszcze dwie zaznaczone strzałki.
Próba do drugiego zadania
1.W każdym wieloboku musi być wpisana przynajmniej jedna cyfra.
2.Każdy wielobok należy wypełnić tyloma cyframi, jaka jest wartość cyfry w tym wieloboku wpisanej (np. jeżeli jest wpisane 4 to w wieloboku należy wpisać 4 czwórki).
3. Jeżeli w wieloboku nie ma żadnej cyfry wówczas należy wpisać w niego maksymalną dopuszczalną cyfrę (np. jeżeli można wpisać 1 i 2 to należy wpisać 2).
4.W każdym kwadracie, złożonym z czterech położonych obok siebie kratek, można wpisać nie więcej niż 3 cyfry (różne lub takie same).
5. Pola wypełnione takimi samymi cyframi, położone w różnych wielobokach nie mogą stykać się bokami (rogami mogą).
Musi być przynajmniej jeszcze jeden warunek, lub któryś z powyższych powinien być inaczej sformułowany, ponieważ przy podanych wyżej ograniczeniach zadanie ma więcej niż jedno rozwiązanie.
Pozdrowienia Antyp
Komentarze z rozszyfrowanymi wszystkimi lub prawie wszystkimi regułami oraz z rozwiązaniami zadań uwolnię w niedzielę w samo południe.
Pozdrawiam deszyfrantów „induktorów”
Jeśli chodzi o drugie zadanie to na razie udało mi się znaleźć następujące reguły:
1. W każdym wyodrębnionym grubszą linią obszarze znajduje się przynajmniej jedna cyfra.
2. Każdy obszar może, choć nie musi, zawierać puste pola.
3. Wszystkie cyfry wpisane do danego obszaru są jednakowej wartości.
4. Ilość cyfr wpisanych w dany obszar jest równa wartości tych cyfr (czyli jedna jedynka, dwie dwójki, trzy trójki itd…).
5. W każdym kwadracie 2×2 znajduje się przynajmniej jedno puste pole.
6. ???…
Czegoś jednak jeszcze brakuje, bo przykład miałby trzy rozwiązania (puste pole w obszarze położonym w prawym dolnym rogu mogłoby znajdować się gdziekolwiek, pozostałe obszary wychodzą jednoznacznie).
Stosując te zasady w zadaniu udało mi się dość łatwo wypełnić ponad połowę diagramu, ale później utknąłem – prawdopodobnie pojawiają się niejednoznaczności spowodowane brakiem jeszcze jakiejś reguły.
Czy ktoś ma jakąś inną koncepcję?
Pozdrawiam
AB
Kto to wie…, może takie rozszyfrowywanie reguł jest nawet ciekawsze od samego rozwiązywania?
Jeszcze jedna znaleziona zasada:
6. Cyfry o tej samej wartości, ale należące do różnych obszarów, nie mogą ze sobą sąsiadować – innymi słowy: jeśli dwa obszary wypełnione takimi samymi cyframi stykają się bokami, to pola, którymi się stykają (przynajmniej w jednym z tych obszarów) powinny być puste.
Przykład wychodzi wówczas w całości w sposób jednoznaczny.
Jeśli dodatkowo zmodyfikuje się jedną z wcześniej zaproponowanych reguł:
5. W każdym kwadracie 2×2 znajduje się przynajmniej jedno, ale nie więcej niż dwa puste pola.
To zadanie można doprowadzić do końca, z tym, że biorąc pod uwagę wszystkie kombinacje, rozwiązań jest dwadzieścia (o ile nie pomyliłem się w liczeniu).
Czyli dalej jeszcze chyba czegoś brakuje.
Pozdrawiam
AB
Zadanie numer 1 jest skonstruowane prawidłowo i ma tylko jedno rozwiązanie.
(podaję cyfry zakreślone, cyfry nie zakreślone oznaczam przez „_”)
3 4 _ _ 4 3
_ 3 3 2 1 4
_ _ 2 3 2 _
_ 2 2 2 _ 1
_ 3 3 2 3 4
_ 3 1 4 3 _
Myślę że zadanie byłoby bardziej eleganckie gdyby w w rozwiązanym układzie wszystkie cyfry zawierające prawidłowe dane były zakreślone na czerwono, a nie zakreślone pozostały tylko te cyfry które zawierają dane nieprawdziwe. Tak jednak nie jest – wśród nie zakreślonych cyfr znajdują się również takie które zawierają prawidłową informację. Nie wiem jednak czy takie reguły nie ułatwiłyby zbytnio procesu rozwiązywania.
A jednak pomyliłem się: przy podanych przeze mnie regułach rozwiązań wychodzi „tylko” 😉 dziesięć.
Pozdrawiam
AB
Panie Marku, mam pewne pytanie i związaną z tym propozycję dotyczące drugiej łamigłówki:
Czy ktoś już odgadł całkowicie jakie są jej reguły? (bo z tego co zrozumiałem, również Panu nie są one znane do końca).
Jeśli tak, to dalszy ciąg tej wypowiedzi nie ma specjalnego sensu (widać jest to do przejścia 😉 ).
Jeśli jednak nie, to może by tym razem ujawniać komentarze z pomysłami na zasady tej zagadki. I zarazem propozycja skierowana do innych by przysyłali to, co im przychodzi do głowy, niekoniecznie od razu komplet ;-).
Nie twierdzę, że ujawnianie należałoby zrobić natychmiast, ale dobrze byłoby tak, aby jeszcze móc wspólnie nad tym pogłówkować. W końcu mieszanka różnych pomysłów wielu osób (taka „burza mózgów”) może dać całkiem niezłe rezultaty.
I druga sprawa:
Czy posiada Pan rozwiązanie tego zadania (np. z kolejnego numeru pisma).
Wydaje mi się, że w tym przypadku znalezienie reguł jest znacznie większym wyzwaniem niż samo zadanie i gdyby nie udało się ich odgadnąć, to „podpatrzenie” mogłoby dać dodatkowe wskazówki. Sam przykład to jednak trochę mało (co widać choćby w moim poprzednim komentarzu).
Pytanie jeszcze co na to inni? (zarówno w pierwszej jak i drugiej kwestii).
Pozdrawiam
AB
Andrzej69:
Jeszcze nikt całkowicie nie rozgryzł reguł drugiego zadania.
Jeśli w komentarzach, które ujawnię w niedzielę, rozgryzienie się nie pojawi i jeśli do wtorku wspólnymi siłami nic nie zwojujemy, to we wtorek w następnym wpisie zamieszczę rozwiązanie, choć ani mi, ani paru innym osobom znajomość tego rozwiązania niewiele pomogła. Niewykluczone jednak, że po prostu marni z nas deszyfranci.
Na marginesie: w Szczawnicy pojawiła się japońska wycieczka. Snują się markotni, bo cały czas albo pada, albo siąpi. Mógłbym ich rozerwać, prosząc o przetłumaczenie, ale to by było zbyt proste, więc zostawiam takie rozwiązanie jako ostateczność – o ile wycieczka sie nie ulotni.
Jeżeli chodzi o zadanie drugie, to zasady ogólne są – według mnie – następujące:
1. kwadrat 8×8 kratek został podzielony na mniejsze obszary.
2. W każdy z wydzielonych obszarów należy wpisać jedną lub kilka takich samych cyfr, przy czym wielkość cyfry określa ile cyfr znajduje się w danym obszarze (jedna jedynka; dwie dwójki, trzy trójki itd)
3. Obszar nie może pozostać pusty (zatem we wszystkie obszary składające się z jednej kratki trzeba wpisać jedynkę)
4. dwie identyczne cyfry mogą ze sobą sąsiadować wyłącznie w przypadku jeżeli należą do tego samego obszaru.
4. pola z cyframi nie mogą tworzyć kwadratu 2×2
5: pola z cyframi powinny tworzyć jeden ciąg pól stykających się ze sobą co najmniej jednym bokiem
Poniżej rozwiązane spełniające ten warunek
4 4 4 4 3 _ 3 3
_ 1 _ _ 5 3 _ 3
_ 2 _ _ _ 3 _ 1
2 1 _ 6 _ 5 1 4
1 _ 6 6 5 5 _ 4
_ 6 6 _ 5 _ 4 4
1 6 _ 2 2 _ 2 _
2 _ 2 1 _ 1 2 1
Niestety w rozwiązaniu jest jeden blok pustych pól o rozmiarze 2×2. Można oczywiście troszkę zmodyfikować rozwiązanie (przez inne rozłożenie piątek) ale wtedy z kolei obszar z cyframi nie będzie ciągły (powstaną dwa albo nawet trzy podobszary)
Być może istnieje jeszcze inna droga postępowania – na razie ta mi się nasunęła. Na pewno bardzo pomocne by było zobaczyć rozwiązanie autorskie, które z tego co wiem Pan posiada.
Pierwsza zagadka jest stosunkowo prosta (jak też zasady , którymi należy się kierować) . Chodzi o to , żeby zakreślić niektóre z cyfr tak , aby każda strzałka zakreślonej cyfry pokazywała ile jest w tym kierunku zakreślonych cyfr . A rozwiązanie to :
o,o,x,x,o,o
x,o,o,o,o,o
x,x,o,o,o,x
x,o,o,o,x,o
x,o,o,o,o,o
x,o,o,o,o,x
A druga zagadka to naprawdę twardy orzech .
Pozdrowienia
Panie Marku myślę, że zaproponowane przez Pana wyjście jest bardzo dobre, tzn.: do niedzieli zmagamy się samodzielnie, później do wtorku wspólnymi siłami, a od wtorku „wsparci” dodatkowo rozwiązaniem. Wg mnie może się ono jednak przydać – jeśli nie w sposób bezpośredni, to chociażby do obalania niektórych fałszywych reguł, a to – wbrew pozorom – dużo.
Pozdrawiam
AB
P.S. A może poprosić wycieczkowiczów o przetłumaczenie na piśmie i nie czytać tego co napiszą? (chyba się Pan oprze pokusie? 😉 ). A wówczas nie trzeba będzie się obawiać, że wycieczka się ulotni.
Niemal równocześnie z rozwiązaniem sejmu pojawiło się rozwiązanie drugiego zadania, czyli przede wszystkim ustalenie jego zasad – wszystko wskazuje na to, że poprawne, choć jego autor, San Rokiz, ma pewne wątpliwości.
Z ujawnieniem rozwiązania wstrzymam się jednak do niedzieli. Może jeszcze ktoś poradzi sobie samodzielnie z tą łamigłówką indukcyjną.
Witam.
Przedstawiam swoją propozycję rozwiązania zadania nr 2.
Reguły:
1. do wszystkich wielokątów w diagramie należy wpisać cyfry od 1 do 6 w taki sposób, aby ilość cyfr w wielokącie była równa wartości danej cyfry (w jednym wielokącie występują jednakowe cyfry);
2. pola z cyframi o tej samej wartości, ale należące do różnych wielokątów nie mogą stykać się bokami (rogami mogą);
3. nigdzie w diagramie nie może wystąpić kwadrat 2×2 wypełniony samymi cyframi;
4. puste pola nie mogą dzielić diagramu na części (pola z cyframi tworzą rozgałęziony wielokąt).
Rozwiązanie zadania według powyższych reguł wygląda następująco (rzędami od góry, z lewej do prawej, „podkreślnik” – puste pole):
4 4 4 4 3 _ 3 3
_ 1 _ _ 5 3 _ 3
_ 2 _ _ _ 3 _ 1
2 1 _ 6 _ 5 1 4
1 _ 6 6 5 5 _ 4
_ 6 6 _ 5 _ 4 4
1 6 _ 2 2 _ 2 _
2 _ 2 1 _ 1 2 1
Pozdrawiam
Piotr
Zmobilizowany informacją o rozgryzieniu przez kogoś drugiej łamigłówki, postanowiłem zrobić jeszcze jedno podejście do tematu. I chyba (trochę już rzutem na taśmę 😉 ) udało mi się odgadnąć jej reguły, a dokładniej, to brakującą ostatnią, ale chyba najważniejszą:
7. Wszystkie pola z cyframi powinny być ze sobą połączone, czyli tworzyć jeden (choć bardzo rozgałęziony) wielobok.
Pozostałe, podane w poprzednich moich komentarzach, zasady wydają mi się prawidłowe, z jednym wyjątkiem: ta oznaczona nr 5 (mówiąca o pustych polach w kwadratach 2×2) pozostaje w pierwotnej postaci (czyli przynajmniej jedno, ale bez ograniczenia do co najwyżej dwóch).
Nie wiem, czy udało mi się odtworzyć identyczne reguły jak w oryginale, ale pasują one do przykładu, który wychodzi w całości w sposób jednoznaczny. Co najważniejsze jednak, tak samo udaje się rozwiązać zadanie 🙂 (przesyłam je w osobnym komentarzu). Oczywiście nie wiem, czy to rozwiązanie pokrywa się z oficjalnym, ale na pewno jest tylko jedno.
Podsumowując podaję komplet zasad:
1. W każdym wyodrębnionym grubszą linią obszarze znajduje się przynajmniej jedna cyfra.
2. Każdy obszar może, choć nie musi, zawierać puste pola.
3. Wszystkie cyfry wpisane do danego obszaru są jednakowej wartości.
4. Ilość cyfr wpisanych w dany obszar jest równa wartości tych cyfr (czyli jedna jedynka, dwie dwójki, trzy trójki itd…).
5. W każdym kwadracie 2×2 znajduje się przynajmniej jedno puste pole.
6. Cyfry o tej samej wartości, ale należące do różnych obszarów, nie mogą ze sobą sąsiadować – innymi słowy: jeśli dwa obszary wypełnione takimi samymi cyframi stykają się bokami, to pola, którymi się stykają (przynajmniej w jednym z tych obszarów) powinny być puste.
7. Wszystkie pola z cyframi powinny być ze sobą połączone, czyli tworzyć jeden (choć bardzo rozgałęziony) wielobok.
Pozdrawiam
AB
A oto moje rozwiązanie drugiego zadania („x” oznacza puste pole):
4 4 4 4 3 x 3 3
x 1 x x 5 3 x 3
x 2 x x x 3 x 1
2 1 x 6 x 5 1 4
1 x 6 6 5 5 x 4
x 6 6 x 5 x 4 4
1 6 x 2 2 x 2 x
2 x 2 1 x 1 2 1
Pozdrawiam
AB
Witam
Oto dwa orzeszki (o włoskich słyszałem, ale o japońskich…?):
1.
Strzałki, z cyfrą oznaczoną kółeczkiem, wskazują ilość oznaczonych kółeczkami cyfr jakie wskazuje cyfra na strzałce.
Uzupełnić diagram kółeczkami tak, aby spełniony był warunek z pierwszego zdania.
2.
– w każdy oznaczony grubą kreską wielokąt diagramu wpisać tyle razy taką cyfrę jaka w nim się znajduje (jeśli cyfry nie ma to należy ją ustalić samemu);
– takie same cyfry z różnych wielokątów nie mogą stykać się bokami;
– kwadraciki jednostkowe diagramu tworzące kwadraty 2×2 nie mogą składać się z samych cyfr (musi być co najmniej jedno puste pole);
– puste pola nie mogą odcinać grupy cyfr (wszystkie pola z cyframi muszą tworzyć jeden wielokąt).
Pozdrawiam
PS
Szkoda, że nie jestem smętnie snującym się turystą przemierzającym wzdłuż i wszerz (patrząc na mapę, częściej wzdłuż) Japonię.
Dla drugiego zadania proponuję następujące zasady :
– w każde pole zakreślone grubą linią wpisz takie same cyfry , w takiej ilości jaka jest ich wartość (np. jedną jedynkę , dwie dwójki , trzy trójki itd.)
– w każdym polu 2×2 mogą być dwie albo trzy cyfry , ale jeżeli są dokładnie dwie i są takie same , to nie mogą być po przekątnej , ale obok siebie .
Niestety mam wątpliwości , ponieważ powyższe reguły w sposób jednoznaczny prowadzą do rozwiązania małego zadania , ale niestety nie dają jednego rozwiązania zadania z diagramu 8×8 .
No cóż , rozwiązanie tego problemu wydaje się dużo trudniejsze niż rozwiązanie Sejmu 🙂
Pozdrowienia i czekam na rozwiązanie
Witam ponownie.
Rozwiązanie zadania nr 1:
W diagramie należy zaznaczyć (czerwone okręgi) niektóre cyfry w strzałkach w taki sposób, aby ilość zaznaczonych cyfr była równa cyfrze zakreślonej w strzałce, która na nie wskazuje (w rzędzie/kolumnie).
Rozwiązanie zadania według powyższej zasady wygląda następująco (podaję zakreślone cyfry rzędami od góry, od lewej do prawej, cyfry nie zakreślone zastąpiłem „podkreślnikami”):
3 4 _ _ 4 3
_ 3 3 2 1 4
_ _ 2 3 2 _
_ 2 2 2 _ 1
_ 3 3 2 3 4
_ 3 1 4 3 _
Pozdrawiam
Piotr
P.S. Jeśli podane przeze mnie zasady rozwiązania zadania nr 2 są poprawne, to można zauważyć podobieństwo tej łamigłówki do zadań znanych jako „Stawy i grobla”. Groblę (o szerokości 1 kratki) w tym przypadku tworzą pola z cyframi.
Piotr
Moim zdaniem instrukcja do zadania drugiego powinna wyglądać tak:
Wypełnij część pustych pól diagramu liczbami według następujących zasad:
– w każdym z obwiedzionych grubszą linią obszarów liczby nie mogą być różne
– w każdym z obszarów występuje tyle liczb, ile wynosi liczba wpisana w ten obszar
– w każdym obszarze musi być wpisana co najmniej jedna liczba
– w dwóch polach sąsiadujących bokiem i należących do różnych obszarów nie mogą znajdować się takie same cyfry.
– w każdym kwadracie 2×2 co najmniej jedno pole musi być puste
– pola z wpisanymi cyframi muszą tworzyć jedną całość.
Panie Marku, z tego co policzyłem, to pięć osób przysłało komplet reguł dla drugiego zadania, które (jeśli pominąć stylistykę) w sumie się od siebie nie różnią. Z tej piątki, trzy podały rozwiązania (pozostałe dwie pewnie też rozwiązały, tylko nie nadesłały), które również są takie same.
Pytanie – dla upewnienia się – czy te rozwiązania pokrywają się z tym, które Pan posiada?
P.S. Było już „sudokuro”. Co Pan sądzi o nazwach jak te podane poniżej? 😉
Do Piotra44:
Też zauważyłem to podobieństwo, o którym piszesz, z tym, że moim zdaniem, ta łamigłówka jest swoistą krzyżówką nurikabe (japońska nazwa „stawów i grobli”) i filomino. Pola z cyframi tworzą groblę jak w nurikabe, ale dodatkowo podlegają zasadom filomino (np. brak możliwości styku bokami obszarów z jednakowymi cyframi). Może by to zadanie ochrzcić jako „filokabe” czy „nurimino”? 🙂
Albo „filonuriminokabe”? 😉
Do San Rokiza:
Gratuluję rozgryzienia reguł jako pierwszy (dzięki temu sam też się zmobilizowałem 🙂 ). Natomiast wydaje mi się, że niepotrzebnie obawiasz się kwadratu z samymi pustymi polami – zasada (jak zresztą sam również napisałeś) dotyczy po prostu wyłącznie pól z cyframi. Zwróć też uwagę jak to wygląda w nurikabe (P.S. Piotra44 i moja, zamieszczona powyżej, odpowiedź). Tam ograniczenie 2×2 dotyczy tylko grobli, a stawy mogą mieć kształty dowolne.
Pozdrawiam
AB
Do Andrzeja69:
Oczywiście, piątka z Łamiblogu trafiła w dziesiątkę!
Nieco więcej na ten temat, a także o propozycjach na chrzciny -w jutrzejszym wpisie.
Pozdrawiam
Do Andrzeja69: sadzę, że Japończycy już nazwali jakoś to drugie zadanie i nie ma co wyważać otwartych drzwi (kilka lat temu rozwiązywało się niektóre zadania logiczne i człowiek nie miał pojęcia, że to np. „Sudoku” albo „Kakuro”).
Pozdrawiam
Piotr