Moja Słowacja
Andrzej Stasiuk pisze o swojej Słowacji. Czytam z zainteresowaniem, bo lubię Stasiuka, ale też z pewnym wzruszeniem, bo mam tak samo, może nawet bardziej – 10 minut rowerem do granicy, którą przekraczam przynajmniej dwa razy w tygodniu. Moja Słowacja leży od Stasiukowej na zachód (Stara Lubowna, Kieżmark, Poprad), ale i do Bardejowa czasem zajeżdżam. Również mam słabość do tego kraju, a szczególnie do mojego regionu, bo to tak blisko, a klimat z różnych powodów zmienia się na wyraźnie łagodniejszy. Stasiuk bardzo ładnie i sugestywnie opisuje tę zmianę, ale gdy czytam „bajkę” o Cyganach, to mu zazdroszczę punktu widzenia i wizji. Zapewne odbierałbym to podobnie, gdyby nie zdarzyło mi się wjechać rowerem na słowackim pustkowiu w grupę kilkudziesięciu półnagich, podchmielonych Cyganów idących całą szerokością drogi, gdybym nie obserwował kilkakrotnie słowacko-cygańskich awantur i przepychanek i jeszcze paru gdybań. Na co dzień antagonizmów się nie czuje, bo jedni i drudzy mają usposobienie raczej pogodne, ale gdy rozmawiam ze znajomymi Słowakami i pojawia się temat ich śniadych sąsiadów, to potrafią soczyście zakląć.
Przepraszam za ten wstęp nie na temat, ale u naszych sąsiadów pozostaję.
Słowacy to ludek bardziej od naszego stadny, życzliwie spontaniczny i towarzyski, a więc lubiący gimnastykować szare komórki grupowo. Kluby główkołamaczy są w kilkudziesięciu miastach, a ich członkowie spotykają się co roku na wielu różnego rodzaju zawodach i turniejach. Część z nich stanowi eliminacje do łamigłówkowych mistrzostw kraju i świata oraz do podobnych mistrzostw w sudoku. Śledzę plan tych imprez i jeśli któraś organizowana jest w moim regionie, staram się na nią dojechać. Warto nie tylko dla łamigłówek, także dla przyjemnej familijnej atmosfery.
Tegoroczny finał mistrzostw Słowacji miał miejsce w lipcu w Svinnej koło Trenczyna. Niespodzianek nie było. Zwycięzca – Peter Hudák i drugi na mecie – Štefan Gašpár to od kilku lat filary reprezentacji, którzy tym samym zapewnili sobie start w październikowych mistrzostwach świata w Rio.
Poniżej para łamigłówek wiązanych, ze słowackiego finału.
Kub i kubiki
Sześcian na rysunku można podzielić na cztery plastry 4x4x1 lub dwa 4x4x2.
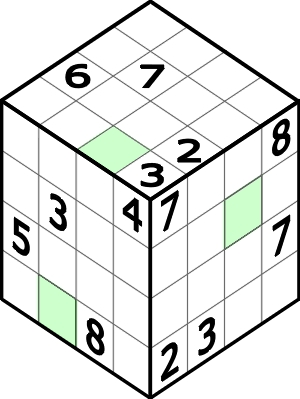
Do pustych kratek należy wpisać cyfry od 1 do 8 tak, aby po podzieleniu sześcianu na plastry jednakowej grubości w dowolny sposób, osiem różnych cyfr znajdowało się na dwóch ściankach 1×4 każdego wąskiego plastra lub na każdej ściance 2×4 grubego plastra (wszystkie niewidoczne ścianki sześcianu i sześcianików są i pozostają oczywiście puste).
Ale, ale… jednoznaczne rozwiązanie tego zadania nie jest możliwe bez wpisania w zielone pola trzech cyfr – tych, które tworzą liczbę będącą rozwiązaniem poniższej łamigłówki.
Z sześcianu usunięto część z 216 tworzących go sześcianików, zabierając kolejno po jednym sześcianiku – zawsze z wierzchu. Proszę ustalić na podstawie rysunku, jaka największa możliwa liczba sześcianików pozostała.
Mam słabość do Słowacji także z pewnego osobliwego powodu: w tym kraju znalazłem odpowiedź na jedno z najważniejszych egzystencjalnych pytań:
Čo bolo skôr, kura alebo vajce?
Bez żartów, na to pytanie można udzielić całkiem poważnej i jednoznacznej odpowiedzi. Kto potrafi?

Komentarze
Naprawdę fajne. Sześcian rozwiązuje się dosyć łatwo, ale miałby dwa rozwiązania, gdyby nie druga zagadka. A przy tej drugiej trzeba być naprawdę spostrzegawczym. Ujęcie częściowo rozebranego sześcianu jest tak niefortunne (oczywiście celowo), że można się łatwo pomylić się przy liczeniu. Proponuję najpierw policzyć ile małych sześcianików miał na początku :)) Przyjemnej zabawy
Drogi Alku,
Policzyć z ilu sześcianików składał się na początku ten sześcian można. Pytanie tylko po co, skoro w tekście nad zadaniem mamy napisane, że było ich 216. Masz rację, do tego zadania trzeba być naprawdę spostrzegawczym. Taka moja drobna złośliwość 😉
A sześcianików pozostało 141 w następującym układzie:
6 6 6 5 4 3
6 5 5 3 3 2
6 5 4 3 3 2
5 5 6 5 4 1
3 4 4 5 4 2
1 1 2 3 4 5
A do tego jeszcze dodam, że najmniejsza ilość sześcianików jaka mogła pozostać to z kolei 125.
Nadsyłane rozwiązania uwolnię w piątek.
W przypadku pytania „co było pierwsze, jajko czy kura?” chodzi oczywiście nie tyle o samą odpowiedź, co o jej sensowne, poważne uzasadnienie.
Odpowiedź brzmi: jajko.
Proszę uzasadnić.
mp
Jak liczyć te kostki, skoro u dołu na prawo od krawędzi jest jakieś wgłębienie. A w tekście napisano, że kostki były usuwane z wierzchu. Dziwne.
sj
Do Sylvii:
Moje pierwsze podejście do sześcianu z małych sześcianików również zakładało „dziurę” z prawej strony. W tej sytuacji udało mi się uzyskać układ najzupełniej prawidłowy w sensie geometrycznym, tyle że nie spełniający przeoczonego warunku, że sześciany usuwane były zawsze z wierzchu. Dopiero gdy wynik nie pasował mi do pierwszej łamigłówki, to po sprawdzeniu treści stwierdziłem, że to założenie było błędne.
Otóż istnieje jeszcze drugi układ sześcianików (nie licząc mutacji polegających na prostym ujmowaniu w miejscach niewidocznych), który również jest prawidłowy geometrycznie, ale spełnia także ten wspomniany wcześniej warunek i którego rezultat pasuje do sześcianu „sudokopodobnego” (choć wymaga to zabrania trochę większej ilości kostek).
Pozdrawiam.
AB
Podaję moje rozwiązania:
1. Sześcian „sudokopodobny”:
góra (patrząc od prawej):
4,6,2,3
5,8,7,1
1,7,6,4
3,2,8,5
ściany boczne:
1,6,2,4,7,5,3,8
8,3,5,7,6,4,1,2
5,2,3,6,8,1,4,7
7,4,8,1,2,3,5,6
Niejednoznaczność pojawiała się w centrum (4 pola) prawej ściany i do tego potrzebny był wynik drugiego zadania.
2. Sześcian „kostkowy”:
wysokości poszczególnych „słupków” (patrząc od prawej):
1,3,5,6,6,6
1,4,5,5,5,6
2,4,6,4,5,6
3,5,5,3,3,5
4,4,4,3,3,4
5,2,1,2,2,3
razem daje to 141.
Najwięcej zamieszania wprowadza moim zdaniem czwarty słupek od lewej w trzecim rzędzie.
3. Jajko czy kura?
Jajko – z uwagi na to, że jaja były znoszone chociażby przez gady, które pojawiły się na Ziemi dużo wcześniej niż ptaki.
(PIERWSZA POPRAWNA ODPOWIEDŹ – mp)
Pozdrawiam.
AB
Dlaczego jajko pierwsze? – tym razem nie całkiem na poważnie ;-).
Aby znaleźć odpowiedź na to filozoficzne, od wieków nurtujące pytanie, należałoby sięgnąć do mądrych ksiąg jak słowniki czy encyklopedie.
A więc bierzemy taką księgę, otwieramy na haśle „jajko” i na haśle „kura”.
I od razu widać, że jajko występuje wcześniej :-).
Pozdrawiam.
AB
Zadanie pierwsze ma dwa rozwiązania. Cyfry wpisane w zielone pola od góry do dołu to 1,1,4 lub 1,4,4.
Zadanie drugie wygląda mi na żart z łamigłówkarzy. Rysunek nie przedstawia rzeczywistej bryły, więc nie może być mowy o policzeniu jej elementów składowych. Jest to jeden z przykladów figur niemożliwych.
Pozdrawiam.
Swego czasu żona przygotowywała coś w kuchni, siedziałem wtedy przy stole i coś mnie tak wzięło by zadać jej to pytanie, tak dla żartu, a ona z całą powagą odpowiedziała:
„Oczywiście, że jajko, Ty wiesz ile się kura gotuje?” 😉
A ja poważnie odpowiem: pierwsze było jajko, bo z jaj wykluwały się dinozaury, a te jak powszechnie wiadomo, były wcześniej od kur.
Witam.
Z sześcianu 6x6x6 usunięto 72 sześcianiki, czyli pozostało ich 144:
1 należy wpisać w zielone pole na górnej ścianie pierwszego sześcianu, a 4 w zielone pola na ścianach bocznych – wtedy zadanie będzie miało jedno rozwiązanie.
Pozdrawiam
Piotr
Do Łukasza :
Oczywiście mój błąd . Chodziło mi o to , aby policzyć wymiary początkowe rozbieranego sześcianu (6x6x6) i zauważyć , że tylne stosy sześcianików nie mogą mieć po osiem klocków i że trzeba zwrócić uwagę na to w jakiej perspektywie pokazano ten układ . Moje rozwiązanie to też 141 sześcianików , ale warunek aby wyjmować tylko sześcianiki z wierzchu determinuje ilość sześcianików z zakrytych kolumn i wynik 125 na pewno jest nie do przyjęcia , co zauważam również bez złośliwości 🙂
Pozdrowienia
Alek
Do Alka:
W zadaniu było napisane, żę należy wskazać ile maksymalnie sześcianików pozostało i wynik ten to oczywiście 141. Na przedstawionym rysunku kilku kolumn w ogóle nie widać i rozwiązanie 125 dotyczyło takiej wersji zadania, w której zamiast największej możliwej liczby należałoby podać najmniejszą możliwą ilość sześcianików na przedstawionym obrazku (oczywiście zachowując pozostałe założenia, tj. ściągania sześcianików z wierzchu).
Może sprawdzisz, czy to rzeczywiście 125?
Do Łukasza :
Problem leży zapewne w tym , że ja nieco inaczej rozumiem warunek „ściągania sześcianików z wierzchu” Jeżeli mamy niewidoczną kolumnę o maksymalnie trzech sześcianikach i otoczoną przez kolumny z ilością sześcianików 3,3,3,5,4,6,5,4 to według mnie nie może być ona „wybrana” do zera , a ma dokładnie 3 sześcianiki . Spróbuj wyciągnąć następny klocek – uważam , że jest „schowany” przez sąsiednie kolumny i nie jest na wierzchu . No chyba ,że spróbujesz pomóc sobie gumą do żucia 🙂
Pozdrowienia
Witam
Poznaliśmy kilka mniej lub bardziej zabawnych odpowiedzi na pytanie „co było pierwsze (lub drugie), kura czy jajko” i może już czas Panie Marku na poważną odpowiedź na nie mniej poważne pytanie nurtujące Wszechświat.
Pozdrawiam
Panie Andrzeju, poważnej właściwej odpowiedzi udzieliły dwie osoby (powyżej) – Andrzej69 i bartover.
Odpowiedź ta wynika z faktu, że w pytaniu nie jest uściślone, że chodzi o jajko kurze.
Do Alka!
No ba, i tu koń pogrzebany. Bo jak dla mnie jeśli tylko do sześcianika jest dostęp z góry, to można go ściągnąć. A w jaki sposób? Naklejanie gumy do żucia? Wyciąganie magnesem? Zasysanie a choćby i odkurzaczem?
No cóż, zadanie nie definiuje w jaki sposób mają być one ściągane, więc nie wprowadzałbym dodatkowego ograniczenia w postaci dostępu do sześcianika z boku.
No cóż . Moja wiedza empiryczna (z okresu zabawy z klockami w dzieciństwie) , w połączeniu z wiedzą teoretyczną na temat grawitacji i sił tarcia (nabyta w okresie późniejszego uczęszczania do szkół) skłoniły mnie do takiej praktycznej interpretacji ściągania klocków z wierzchu . No bo inaczej rozwinięcie tego warunku brzmi nieco absurdalnie – ściagaj klocki z wierzchu odkurzaczem , bo jak wyciągniesz od spodu to się nie obsuną , ponieważ nie działa powszechne prawo ciążenia , albo tarcie klocków jest tak duże , że mogłaby powstać pustka z podstępnie wyciągniętego od spodu klocka !
Ale zgadzam się , że jest to z mojej strony nadinterpretacja . W końcu problemy matematyczne często opierają się na nieco wydumanej „rzeczywistości” a nie na podejściu praktycznym .
Pozdrowienia i bez urazy
Alek
Kura to też dinozaur, tylko mały.