Nonet czworaczków

1 lutego 2025
Marek Penszko

Znajoma pani matematyk zwróciła mi uwagę na sprytny sposób podejścia do zadania z poprzedniego wpisu. Przypomnę: chodziło o wpisanie do pól kwadratu 3×3 liczb od 1 do 9 w taki sposób, aby suma czterech liczb w każdym z czterech czworaczków, czyli subkwadratów 2×2, była liczbą pierwszą (na razie pomijamy hetmańską kolejność liczb). Sposób oparty jest na dwóch oczywistych faktach:
– każda liczba pierwsza jest nieparzysta;
– suma czterech liczb jest nieparzysta tylko wtedy, gdy nieparzysta jest dokładnie jedna z tych liczb lub dokładnie trzy.
To wymusza warunek: każdy subkwadrat powinien zawierać jedną lub trzy liczby nieparzyste (N).
Pierwszy etap rozwiązywania polega więc na takim rozmieszczeniu pięciu liter N w diagramie, aby powyższy warunek był spełniony. Okazuje się, że takie rozmieszczenia (całkowicie różne, czyli pomijając obroty i odbicia) są tylko trzy:

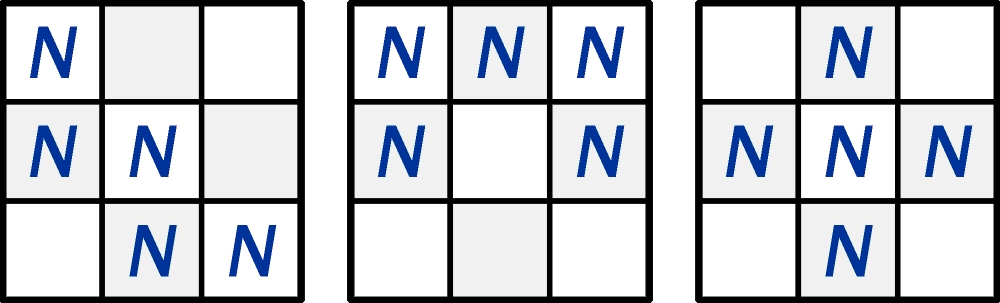
Teraz dopiero można przystąpić do prób i błędów, czyli wpisywania liczb – w szczególności kolejnych ruchem hetmana szachowego. Zadanie jest prostsze po zauważeniu, że jeden z powyższych schematów „nie działa” dla wersji hetmańskiej (który?).
Kuszące wydaje się powiększenie diagramu o jedno „oczko” – do formatu 4×4. Tylko że wtedy zadanie robi się ekstremalnie żmudne – praktycznie nie do ruszenia bez wsparcia komputerowego (zwłaszcza gdy chodzi o znalezienie wszystkich rozwiązań); liczb jest wówczas 16, czworaczków dziewięć (czyli nonet), a zakres sum w czworaczkach obejmuje tuzin liczb pierwszych – od 11 do 53.
Można jednak (pomijając hetmańską kolejność) skorzystać z podanego wyżej sposobu i poszukać schematów koniecznego rozmieszczenia w diagramie ośmiu liczb nieparzystych – od 1 do 15. Na poniższym rysunku podany jest jeden z takich schematów, a obok odpowiadające mu przykładowe rozwiązanie.

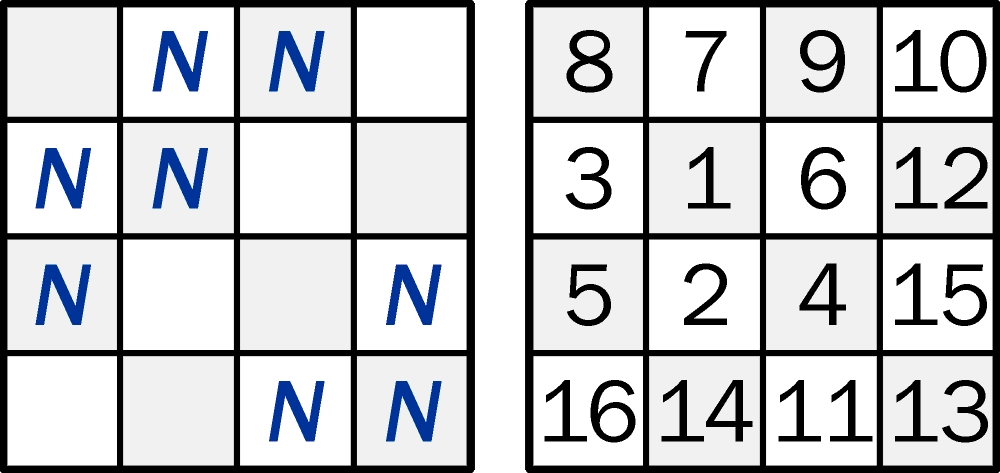
Ile jest wszystkich (całkowicie różnych) schematów takiego rozmieszczenia liczb nieparzystych w diagramie 4×4, aby suma czterech liczb w każdym z 9 subkwadratów 2×2 mogła być liczbą pierwszą?

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.