Kulisy seksu
Chodzi oczywiście o niezdrożny seks grupowy trójnic z łamigłówki konkursowej. W gruncie rzeczy kulisy teorii ujawnił sidelfius we wpisie, który wyczekał się kilka dni na publikację w związku z trwającym konkursem. Wprawdzie autor wpisu zmienił trójnice w ośmiornice, a twierdzenie (wzór) Eulera w tożsamość (tożsamością Eulera nazywa się zwykle coś innego), ale są to drobne figle formalne, natomiast meritum jest tip-top.
Praktycznie najistotniejszy wydaje się wniosek, że w grafie stanowiącym miłosną sieć nie mogą występować trójkątne ściany. W związku z tym, że wzór Eulera dotyczy zarówno grafów planarnych jak i wielościanów, co podkreśla zbieżność terminologii (w obu przypadkach mówimy o wierzchołkach, krawędziach i ścianach), więc, po uwzględnieniu wspomnianego wniosku, rozwiązywanie łamigłówki sprowadzi się do trywialnego zagadnienia: wskazania wielościanu o najmniejszej liczbie wierzchołków, którego żadna ściana nie jest trójkątem. Taka bryła to oczywiście równoległościan, a żeby było elegancko, można wskazać jego postać foremną, czyli sześcian. Teraz wystarczy sześcian „rozpłaszczyć”, a następnie odpowiednio oznaczyć krawędzie wychodzące z każdego wierzchołka, traktując je jak nogi trójnic i – rozwiązanie gotowe.
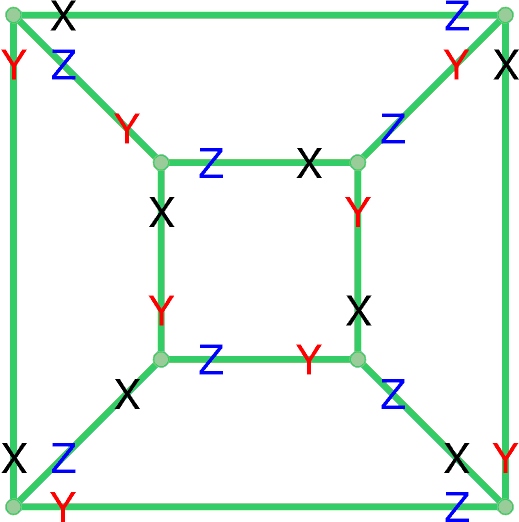
Taki sposób radzenia sobie z łamigłówką jest jednak trochę na skróty. Aby ujawnić w pełni kulisy rozwiązywania, warto podać nieco inną, bardziej praktyczną metodę.
Zacznijmy od tego, że są tylko dwa sposoby sczepienia się trójnicy z nogami trzech innych osobników:
S1: X1-Y, Y1-Z, Z1-X
S2; X1-Z, Y1-X, Z1-Y
I druga konkluzja: jeśli jakaś trójnica połączy się z trzema innymi sposobem S1, to każda z tych trzech będzie połączona z innymi sposobem S2. Uogólniając: każda trójnica S1 (korzystająca ze sposobu S1) łączy się z trzema trójnicami S2 – i odwrotnie. Ponieważ żadna noga nie pozostaje wolna, więc trójnic S1 będzie tyle samo, co S2, a więc łączna liczba wszystkich będzie parzysta.
Teraz można już przystąpić do graficznej symulacji procesu tworzenia się grupy w celu prokreacji. Trójnice będziemy lokować na naprzemianległych „poziomach” S1 i S2, odpowiadających sposobowi łączenia, z którego korzystają.
Najpierw jedna trójnica S1 łączy się z trzema S2.
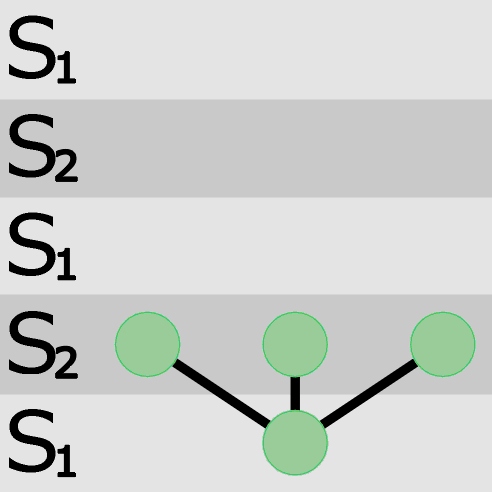
Jeżeli teraz na trzecim poziomie, czyli drugim S1, pojawi się jeden osobnik łącząc się z trzema S2 poniżej, to wprawdzie je „zaspokoi” (nie w pełni), ale równocześnie odetnie możliwość utworzenia trzeciego połączenia środkowej trójnicy.
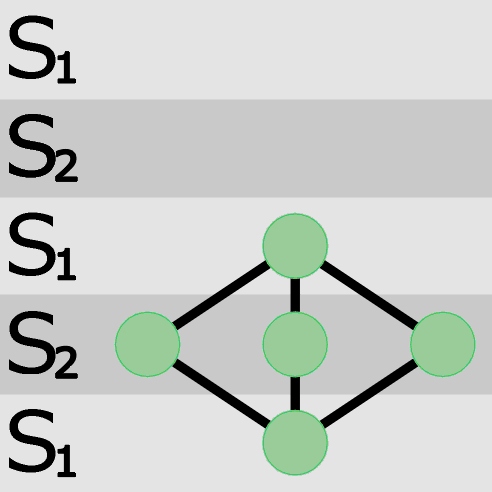
Spróbujmy więc umieścić na trzecim poziomie dwa osobniki i połączyć je z S2.
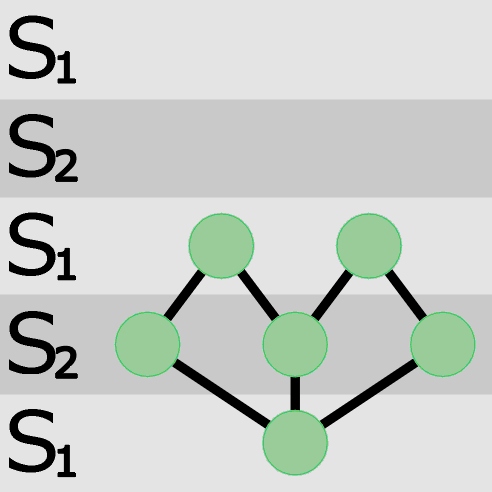
Tym razem wszystko gra, można więc kontynuować tworzenie grupy, przyłączając dalsze trójnice – zgodnie z regułą S1 do S2 i vice versa. Do pełni szczęścia brakuje już tylko dwóch osobników, a doprowadzenie do krótkiej chwili rozkoszy nie nastręcza problemów. Oto ta chwila:
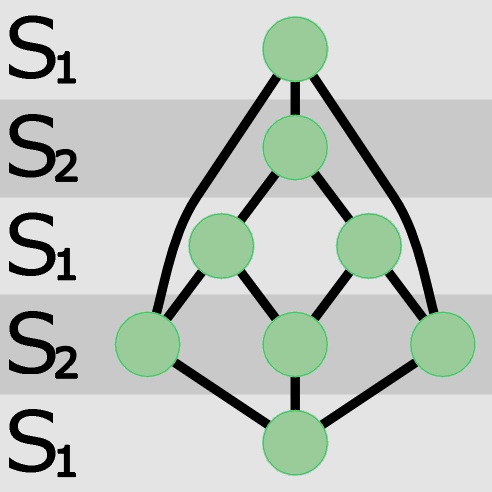
Proszę zwrócić uwagę, że z niemożności łączenia osobników znajdujących się na tym samym poziomie wynika także brak trójkątnych ścian w grafie.
Nieco mniej niż połowę z 73 nadesłanych przez Państwa rozwiązań, stanowiły ładne, zwykle kolorowe rysunki trójnic w niedwuznacznej sytuacji – byłaby z nich całkiem oryginalna wystawa. Ponieważ nagroda-niespodzianka jest zgoła symboliczna, więc mam nadzieję, że wybaczą mi Państwo, iż postanowiłem rozlosować ją wśród kilkunastu wybranych rozwiązań z najładniejszymi, moim zdaniem, rysunkami.
Nagrodę, łamigłówkę River Crossing, ufundowaną przez firmę Logorajd, otrzymuje Pani Aleksandra Golecka. Laureatkę proszę o kontakt pod adresem m.penszko@polityka.com.pl w celu ustalenia sposobu przekazania nagrody.
W sudoku z poprzedniego wpisu, stanowiącym modyfikację jednego z zadań z 2. Mistrzostw Świata, był drobny błąd (brak jednej kropki), poprawiony po uwadze Oystera. To potknięcie nasunęło mi pomysł zaprezentowania łamigłówki ze świadomym błędem, której rozwiązanie polega także na znalezieniu i poprawieniu pomyłki.
Literówka

W dodawaniu czterech liczb 4-cyfrowych cyfry zastąpiono literami. Takie same litery oznaczają jednakowe cyfry, a różnym literom odpowiadają odmienne cyfry. Jedną i tylko jedną cyfrę zastąpiono niewłaściwą literą. Którą oraz jakie są wartości składników i sumy?
Uwaga: w komentarzach są rozwiązania, więc kto chce trochę pogimnastykować szare komórki (zadanie jest łatwe), niechaj przedtem do komentarzy nie zagląda.

Komentarze
Wychodzi na to, że do zmiany kwalifikuje się któraś z pierwszych cyfr składników sumy, dlatego że cztery cyfry nie mogą dawać w wyniku piątej cyfry, bo nawet jak weźmiemy najmniejsze, czyli 1 + 2 + 3 + 4, to nie otrzymamy wyniku jednocyfrowego. Jeśli zmienimy CFBC na DFBC, to otrzymamy:
2148
1346
1146
4248
——
8888
Rozwiązanie
===========
EDBA
CFBC
DDBC
BEBA
———
AAAA
Cztery dodawane liczby zaczynają się różnymi literami.
Przy założeniu, że te litery są poprawne ich suma
wynosi co najmniej 1+2+3+4=10 więc wynik całego
dodawania powinien być pięciocyfrowy. Sprzeczność
dowodzi, że któraś z dodawanych liczb rozpoczyna się
błędną literą.
Znajdujemy wartość litery A.
Na podstawie pierwszej kolumny wnioskujemy, że A>=1+1+2+3=7
(któraś cyfra się powtarza, w minimalnym przypadku jest to 1).
Z kolei na podstawie ostatniej kolumny wnioskujemy, że
[1] A+2C=10k gdzie k=1 lub k=2. Czyli A jest parzysta
i musi być A=8.
Znajdujemy wartość litery C.
Z trzeciej kolumny dostajemy zależność [2] 4B+k=10m+8 dla pewnego m.
Czyli k jest parzyste (k=2) i z równości [1] dostajemy C=6.
Analizując jeszcze raz kolumnę pierwszą widać, że litera C jest
tam błędna, gdyż 1+1+2+6=10 i wynik byłby pięciocyfrowy.
Znajdujemy wartość litery B.
Równość [2] po podstawieniu przyjmuje postać 4B=10m+6, co jest
możliwe tylko dla B=4 i m=1 lub B=9 i m=3.
Drugi wariant należy odrzucić znów ze względu na pierwszą kolumnę
(litera B nie jest tam błędna), czyli B=4.
Po podstawieniu tego co już wiemy reszta zadania sprowadza się
do równości [3] 12D+11E+F+10X=47 (X zastąpiło błędną literę C).
Musi być X=1 oraz D=1,E=2 lub D=2,E=1 (dla innych wartości lewa
strona będzie >50). Czyli 11(1+2)+D+F+10*1=47, co po
skróceniu daje D+F=4.
Koniec końców otrzymujemy D=1, E=2 i F=3.
2148
1346
1146
4248
——–
8888
Witam.
Czy liczby czterocyforwe mogą zaczynać się od 0 (zera)?
Jeśli tak to liczba rozwiązań wzrośnie.
Pozdrawiam
Jak wynika z tekstu zadania na początku było dodawanie czterech liczb 4-cyfrowych. Czy liczba 4-cyfrowa może zaczynać się od zera w zapisie działania w słupku? Czy to będzie liczba 4-. czy 3-cyfrowa? A jeśli z przodu dopisalibyśmy n zer, to czy powstałaby liczba (n+3)-cyfrowa?
Czy to jest ciekawy temat do dyskusji?
🙂 mp
Moim zdaniem wątpliwośc Andrzeja jest jednak uzasadniona, bo w tego typu zadaniach przyjęty jest zwyczaj (inna sprawa, czy sensowny) informowania, że „żadna liczba nie zaczyna się zerem”.
Pozdrawiam
Kleo