Dwuwymiarowy seks grupowy
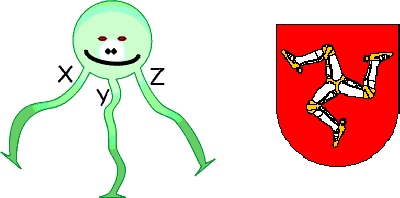
Trójnice należą do niezwykłego gatunku głowonogów rozmnażających się przez kontakt grupowy i to w bardzo osobliwy sposób. W przeciwieństwie do innych mięczaków z tej gromady, które mają osiem lub dziesięć ramion, zwanych potocznie nogami, każda trójnica ma tylko trzy nogi – żeńską (X), męską (Y) i żeńsko-męską (Z) – zaś każda noga zakończona jest odpowiednim organem płciowym. By doszło do grupowego zapłodnienia, końce wszystkich nóg grupy trójnic powinny się zetknąć tak, aby spełnionych było pięć warunków:
1. każda noga każdej trójnicy weszła w kontakt z jedną i tylko jedną nogą innej trójnicy;
2. każda trójnica została dotknięta przez trzy różne nogi (X, Y, Z);
3. każde dwie trójnice stykały się tylko jedną nogą lub nie stykały się w ogóle;
4. nigdzie nie stykały się takie same nogi (X z X, Y z Y, ani Z z Z);
5. nogi nigdzie się ze sobą nie krzyżowały (trójnice są stworami dwuwymiarowymi i wszystko dzieje się na płaszczyźnie);
warto też dodać, że nogi są bardzo rozciągliwe.
Gdy wszystkie powyższe warunki zostaną spełnione, następuje krótka chwila rozkoszy i nagle, jak za dotknięciem czarodziejskiej różdżki, nie wiadomo skąd wśród grupy trójnic pojawia się malutka trójniczka.
Uczeni wciąż badają ten tajemniczy proces, próbując uchwycić moment pojawienia się nowego stworzenia. Większość badaczy przychyla się do hipotezy, że to, co najistotniejsze, zachodzi w czwartym wymiarze, z pominięciem trzeciego, po czym następuje gwałtowny, przypominający eksplozję proces przemiany jakiegoś organizmu przejściowego w wyższym wymiarze, a w konsekwencji nagłe pojawienie się dojrzałej postaci na płaszczyźnie.
Ile co najmniej trójnic musi się zetknąć, aby na świat przyszła nowa trójniczka?
Odpowiedzi można przesyłać pod adresem m.penszko@polityka.com.pl Nie wystarczy jednak podać tylko liczby. Jako rozwiązanie proszę załączyć jakiś symboliczny zapis, schemat lub rysunek grupy trójnic w miłosnym… jak to określić? „Splocie” – nie pasuje, „uścisku” – chyba też nie za bardzo, może więc: „w miłosnej sieci”.
Jak zwał, tak zwał, a do rozlosowania jest atrakcyjna nagroda-niespodzianka. Ponieważ zadanie jest niełatwe, więc niechaj terminem nadsyłania rozwiązań będzie 14 maja (włącznie).
Poniżej: wizerunek trójnicy oraz, jako ciekawostka, jej „kuzyn” – szlachecki herb Drogomir.

Komentarze
Szanowni Rozwiązywacze, po kilku godzinach od opublikowania zadania otrzymałem juz kilkanaście rozwiązań, a wszystkie… błędne i błąd jest zawsze ten sam: pomijają Państwo warunek 2. Zadanie naprawdę nie jest takie proste.
Pozdrawiam
mp
Rezerwuję sobie rozwiązania od 1 do 5000. Schemat wyślę jak się dowiem, który wynik jest prawidłowy. 🙂
Jest to typowy przykład zadania które można rozwiązać
korzystając z tożsamości Eulera F+V=E+2, gdzie
F – liczba ścian, V – liczba wierzchołków, E – liczba krawędzi
w wielościanie wypukłym.
Poprawny układ ośmiornic można wyobrazić sobie jako
rzut takiego wielościanu na płaszczyznę, gdzie głowy ośmiornic
to wierzchołki, a połączenia odnóży to krawędzie. (ścisły tego dowód
wymagałby chyba sięgnięcia do topologii).
Jedyne co trzeba jeszcze zauważyć to fakt, że w takim układzie
nie mogą występować ściany trójkątne (tzn. ośmiornica nie może się
stykać z dwoma ośmiornicami, które się również stykają).
Jako dowód można rozpisać sobie wszystkie przypadki i dojść do
sprzeczności z którąś z zasad (nużące i brzydkie więc szkoda pisać).
Jeżeli przyjmiemy, że F(i) to liczba boków i-tej ściany wielościanu,
a V(i) to liczba krawędzi wychodzących z i-tego wierzchołka, to
korzystając z F(i)>=4 i V(i)=3 (każda ośmiornica ma 3 odnóża)
otrzymujemy zależności:
2E=Suma(V(i))=3V oraz 2E=Suma(F(i))>=4F
Stąd korzystając z tożsamości Eulera łatwo dojść do nierówności V>=8.
Czyli ośmiornic musi być co najmniej 8.
I rzeczywiście tyle wystarcza jeżeli umieścimy ośmiornice w
wierzchołkach sześcianu foremnego (łatwo zrzutować do grafu
planarnego) i odpowiednio poprzypisujemy rodzaje odnóży.
Rysunek (O – głowy ośmiornic, ciekawe jak się porozsuwa?):
OCCCCBBBBO
AB………….AC
A..A………B..C
A….OB.CO…C
A….C…..A…C
C….A…..C…A
C….OC.BO…A
C..B………A..A
CA………….BA
OBBBBCCCCO
No jestem pod wrażeniem … doszedłem do tego samego, bardziej „rzeźbiarską” metodą.
Teorię grafów miałem tak ze 15 lat temu
pozdrawiam
Można na naszkicowanym lekko okręgu umieścić w równych odstępach 6 główek. Z każdej główki wystawić po jednej nóżce w prawo i po jednej nóżce w lewo. Na tym etapie rysunek wygląda tak, jakby dzieci chwyciły się w kółeczku za ręce 🙂 Następnie co druga z tych sześciu trójniczek wstawia nóżkę do środka okręgu, a pozostałe trzy trójniczki wystawiają nóżki na zewnątrz okręgu. W środku okręgu należy dorysować 7 trójniczkę, która chwyci te wstawione do środka nogi, a na zewnątrz dorysować ósmą trójniczkę, która chwyci te nogi wystawione na zewnątrz.
Witam.
Można również narysować dwa okręgi współśrodkowe (o różnych średnicach) i na każdym z nich umieścić po cztery trójnice, a następnie połączyć parami trójnice lażące na wewnętrznym okręgu z odpowiednimi na zewnętrznym. Podobny układ uzyskamy rysując dwa kwadraty (jeden wewnątrz drugiego), a trójnice umieścić w wierzchołkach.
Pozdrawiam
Piotr