Uwież
Na niektórych białych polach należy ulokować wieże szachowe – czyli „uwieżyć” (neologizm bliźniaczy np. z „ukwiecić”) diagram – tak, aby każde białe pole było atakowane przez przynajmniej jedną wieżę, ale by żadna wieża nie atakowała innej. Podobnie jak w szachach – każda wieża atakuje wszystkie pola w wierszu i kolumnie, na przecięciu których się znajduje, w tym także zajmowane pole – jednak tutaj zasięg ataku ograniczają żółte pola. Cyfra w żółtym polu oznacza, w ilu spośród czterech sąsiadujących z nim bokiem pól powinny pojawić się wieże. Wieże mogą także zajmować inne, nie wskazane cyframi pola.
W zadaniu cyfry od 0 do 4 są zaszyfrowane literami od A do E. Takim samym literom odpowiadają jednakowe cyfry, a różnym – różne. Ponadto jedno i tylko jedno pole w diagramie jest nieatakowane – dopisane w sobotnie południe – sorry!
W rozwiązaniu wystarczy podać, ile wież udało się ulokować w diagramie.
Przykład:
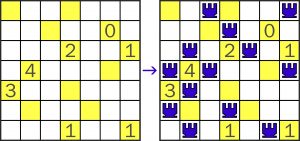

Wypada dodać, że zadanie jest wieżowo-szyfrowym (dość trudnym) wariantem japońskiej łamigłówki Akari, która już kiedyś w Łamiblogu gościła.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Czy zadanie w ogóle ma rozwiązanie?
Jedynie D oraz E mogą mieć wartość 4. Jeśli D=4, to szybko dochodzimy do sprzeczności (musi być wówczas A=0 i żadna litera nie mogłaby odpowiadać trójce). Zatem E = 4. Po rozstawieniu wież wokół E widać, że C = 3 (jedyna opcja dla trójki to C).
I teraz zaczyna się problem.
Załóżmy, że mamy już rozstawione wieże wokół C i E.
Nie może być B = 2, bo wówczas przy literze A na lewo od dwóch D nie mogłaby stać żadna wieża, ale musi być A >= 1 (bo C = 3).
Nie może być A = 2, bo to daje B = 0 (prawy dolny róg), stąd D = 1 i łatwo się przekonać, że białe pole w trzecim wierszu i piątej kolumnie pozostanie nieaatakowane, sprzeczność.
Ale też nie może być D = 2, bo wtedy A = 1 i B = 0, ale wtedy nieaatakowane pozostanie pole nad górną literą D.
Racja! Dopisałem brakujący warunek.
mp
Znalazłem rozwiązanie – musiałem tylko zmienić żółte pole (e7) na białe.
Dopisałem brakujący warunek.
mp
Jeśli się nie pomyliłem gdzieś po drodze, to uwzględniając poprawkę mamy jedno rozwiązanie:
A = 1, B = 0, C = 3, D = 2, E = 4
20 wież w diagramie, nieatakowane pole nad górną literą D.
Ilość wież: 22.
Rozwiązanie niemal po sznurku – z ciekawymi wnioskowaniami.
Właściwie słowo „niemal” mógłbym ominąć.
Jeśli 22, to które pole jest nieatakowane?
mp
https://zapodaj.net/b3034ef1945ed.png.html
Zamiana żółtego pola e7 na białe dawała „naprawę” całego zadania (zielone strzałki pokazują, że wszystkie pola są wtedy atakowane).
Zaproponowana przez Pana zmiana (jedno pole niatakowane) powoduje, że musiałem dodać do rozwiązania wieżę na polu e8.
Nieatakowane pozostaje czerwone c7.
No i zobaczyłem to po sekundzie od wysłania obrazka:
Niestety na polu e8 nie może stać wieża bo (w mojej wersji rozwiązania) B ma zero sąsiadów wieżowych.
Wygląda na to, że będę miał szansę jeszcze się trochę podelektować rozwiązywaniem ?.
20
20 wież
_-pole białe
w-pole z wieżą
#-pole czarne
0,1,2,3,4-pole czarne z liczbą
+-pole nieatakowane
_w1_#_w_#_
#___w__#_w
_0#__0_#w3
__+_#____w
w_2w__#w_1
1_w2__w#__
____w#___w
0_#w4w_##_
_w#_w____0
w#w__#_1w_
No to klops z tym polem, można było tam wrzucić żółty kwadracik (chociaż to by od razu ujawniło czwórkę).
Wyszło mi 20 wież (A=1, B=0, C=3, D=2, E=4).
20 wież; A=1, B=0, C=3, D=2, E=4; pole nieatakowane 4 rząd 3 kolumna
U mnie wyszło 20 wież,
A – 1, B – 0, C – 3, D -2, E -4
Nieatakowane pole to: 4 wiersz, 3 kolumna.
20