Elki
Jeśli w zadaniu w roli głównej pojawiają się elementy w kształcie litery „L”, to jest spora szansa, że jego tytuł będzie taki, jak wyżej. Parę „Elek” trafiło się w Omnibusach, ale w Łamiblogu jeszcze nie gościły. Pora na debiut takiego ich rodzaju, który w moim dorobku dotąd się nie pojawiał, choć jest podobny do zamieszczonego w zimowym Omnibusie przed dwoma laty.
Białą część diagramu należy podzielić na L-działki złożone z czterech kratek, uwzględniając oczywiście także odbicia lustrzane, czyli Г-działki. Żadna elka nie może obejmować szarej kratki.
Przykład
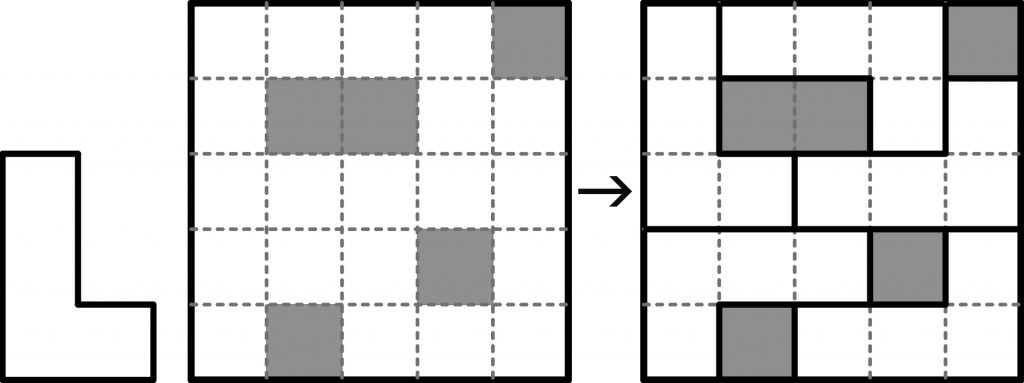
Zadanie

W rozwiązaniu wystarczy podać, ile elek znajduje się w diagramie w takiej pozycji jak litera L w tekście.

Komentarze
Jest ich wszystkich 22.
Dwie z nich są normalne (około 9% populacji).
Czyli dość przyzwoita statystyka.
Są dwie L
2
http://pokazywarka.pl/ykygaj/
Widzę dwie eLki:
http://pokazywarka.pl/dwie_elki/
Przed chwilą kliknąłem „Opublikuj komentarz”, lecz go nie widzę… Więc jeszcze raz:
Są dwie eLki:
http://pokazywarka.pl/dwie_elki/
Ponieważ zadanie było łatwe, to dodajmy cosik:
Wszystkich eLek nie da się pomalować trzema kolorami, potrzebne są cztery. Jeśli ten czwarty kolor będziemy używać najoszczędniej, jak tylko się da, to:
– ile eLek musi być nim pomalowanych?
– na ile sposobów takie kolorowanie można wykonać?
Takie eLki są tylko dwie. Jedna z nich w prawym rogu diagramu, druga
mniej więcej centralnie. Zaczyna się w trzecim wierszu piątej kolumnie i kończy się w piątym wierszu i szóstej kolumnie.
@xswedc
Wystarczy jedna elka inna, ale na ile sposobów – nie wiem. Co najmniej dwa 🙂
W diagramie podstawowym usuwamy dodatkowo cztery białe pola – tak, że tworzą one kwadrat 2×2.
Cel zadania pozostaje bez zmian: trzeba wypełnić białe pola Elkami.
Usunięty kwadrat 2×2 można umieścić dowolnie w obrębie białych pól.
Zastanawiam się, co podpowiada intuicja w takiej sytuacji.
@apartado
Intuicja podpowiada, aby zostawić ją w spokoju. Kolejne eLki wstawia się w sposób jednoznacznie wymuszony (z dokładnością do kolejności), co oznacza, usunięcie czegokolwiek, co nie jest eLką, uniemożliwi rozwiązanie.
Jest jedno rozwiązanie. 2 elki są jak w tekście
@apartado
po wyjęciu kwadratu 2×2 nie da się ułożyć puzzli
Jest jedno rozwiązanie w którym są dwie elki jak w tekście.
@apartado
Po wyjęciu kwadratu 2×2 nie da się ułożyć puzzli.
A jak będzie jeśli przez „diagram podstawowy” będziemy rozumieli kwadrat 10×10 bez żadnych szarych kwadracików i z takiego czystego kwadratu usuwamy kwadracik 2×2. Czy teraz można ułożyć wszystkie 24 elki?
Chyba warto by wskazać miejsce, z którego usuwamy kwadrat 2×2. Bo jeśli z dowolnego, to z wyłożeniem 24 elek nie ma problemu.
mp
Wydaje mi się, że z żadnego miejsca nie możemy wyrzucić bo wyłóżmy naszą posadzkę kafelkami 2×2 z następującym wzorem:
12
34
Wyjmując z dowolnego miejsca kwadrat 2×2 usuwamy zbiór {1,2,3,4}, Natomiast usuwając elkę usuwamy zbiór w którym jedna cyfra się powtarza. A więc kwadrat 10×10 bez kwadracika ma wszystkich cyfr po równo (po 25 sztuk) a w kwadracie bez elki mamy aż trzy różne ilości cyfr. Np 25 jedynek, 23 dwójki oraz 24 trójki i czwórki.
To ja inaczej: dwie elki pokrywają prostokąt 2×4; usuwając z rogu kwadrat 2×2 bez trudu pokryjemy pozostały obszar 12 prostokątami 2×4.
mp
„Chyba warto by wskazać miejsce, z którego usuwamy kwadrat 2×2. Bo jeśli z dowolnego, to z wyłożeniem 24 elek nie ma problemu.”
Można usunąć dowolny kwadrat 2×2 i zawsze rozwiązań są miliony. Jeżeli usuniemy dwa takie kwadraty (nienakładające się) to już nie można ułożyć pozostałej części z Elek.
Wersja zadania z usuwaniem pól:
Z diagramu 12×12 wypełnionego białymi polami usuwamy cztery pola za pomocą poniższej procedury.
Rzucamy dwiema kostkami sześciennymi.
Ilość oczek na każdej z kostek mnożymy przez 2.
Z diagramu usuwamy pole o współrzędnych policzonych w ten sposób.
Kostka1 x 2 =>oś X, kostka2 x 2 =>oś Y.
(Procedurę powtarzamy czterokrotnie).
Jakie jest prawdopodobieństwo, że tak utworzony diagram można wypełnić Elkami?
Nie chodzi mi o dokładnie policzone wartości, ale raczej o ocenę typu: „przeważnie można”, „raczej nie można”, „zawsze można” itp
Czyli: co nam podpowiada intuicja/oszacowanie ?.
Faktycznie można ułożyć 12 prostokątów 2×4, np. tak:
AAAABBBBAA
AAAABBBBAA
BBBBCCCCAA
BBBBCCCCAA
AAAABBBBCC
AAAABBBBCC
BBBBAAAACC
BBBBAAAACC
AAAABBBB
AAAABBBB
Zbyt pochopnie zastosowałem trik z kolorowaniem.
Widać, że zagadnienie jest ciekawe. Czy ktoś zna pokrycie 25 elkami kwadratu 10×10?
Takie pokrycie nie jest możliwe. Prostokąt axb można pokryć elkami tylko wówczas, gdy iloczyn axb jest wielokrotnością 8 (i oczywiście a,b>1).
mp
Białego kwadratu 10×10 nie da się wypełnić eLkami. Ogólniej, żadnego prostokąta o polu P=4*n dla nieparzystego n też się nie da.
Dowód:
Do każdej kratki prostokąta leżącej w wierszu parzystym wpiszmy 0, natomiast do leżącej w wierszu nieparzystym wpiszmy 1. Wtedy suma cyfr z kratek należących do dowolnej eLki jest zawsze nieparzysta (1 lub 3).
Liczba n-1 jest parzysta, więc suma liczb z n-1 eLek też jest parzysta. Dodanie sumy ostatniej n-tej eLki da całkowitą sumę nieparzystą. Tymczasem pole P jest parzyste. Sprzeczność.
Zastanawiam się nad dowodem wypełnialności eLkami dowolnej figury zbudowanej z jednostkowych kwadratów. Zakładam, że pole figury jest spójne, czyli, że od dowolnego kwadratu można dojść do każdego z pozostałych robiąc jednostkowe kroki w poziomie lub w pionie. To oznacza, że figura może mieć zarówno „szare pola” wewnątrz, jak i różnego rodzaju wcięcia, wypustki na obwodzie. Może też nie dać się rozciąć na prostokąty o polu będącym wielokrotnością 8.
Mam w tym tygodniu wyjątkowo mało czasu , więc pokażę tylko kilka początkowych przemyśleń:
Mamy dwa prostokąty, z których w dwóch narożnikach usunąłem po dwa kwadraty. Pola obydwu figur są równe 44, czyli mogą pomieścić po 11 eLek. Którą z nich można wypełnić eLkami?
http://pokazywarka.pl/linka1/
Łatwo to wywnioskować stosując metodę z dowodu przedstawionego wcześniej dla prostokątów: wypełniamy co drugi wiersz jedynkami i liczymy sumę. W lewej figurze wynosi ona 23, a prawej 22. 11 eLek daje sumę nieparzystą, więc można wypełnić tylko figurę lewą (suma 23).
http://pokazywarka.pl/linka2/
Zrobiłem też parę figur z podwójnymi wcięciami i wypustkami. Którą/które z tych trzech figur można zaeLkować?
http://pokazywarka.pl/linka3/
W każdej z nich suma z eLek wynosi 23 lub 25, więc wszystkie!
http://pokazywarka.pl/linka4/
Ale nie rozpędzajmy się… Są też takie figury:
http://pokazywarka.pl/linka5/
Niby suma eLek to 19, a nijak nie da się tego wypełnić! To może tak:
http://pokazywarka.pl/linka6/
Wypełniłem zerami i jedynkami nie tylko wiersze, ale również kolumny. Jest oczywiste, że i tu i tu suma z eLek musi być nieparzysta, tymczasem dla kolumn jest parzysta! – nie ma więc wypełnienia.
To były przypadki geometrycznie proste. Są jednak figury wredne, dla których, mimo prawidłowych sum i wierszach i w kolumnach wypełnienie nie istnieje.
http://pokazywarka.pl/linka7/
Zastanawiam się, jak takie przypadki ująć w sposób sformalizowany, godny umieszczenia w jakimś ogólnym dowodzie. LOL Za twórcze pomysły Ogólnoświatowe Stowarzyszenie ELkowców będzie wdzięczne…
@OlaGM
„Wystarczy jedna elka inna, ale na ile sposobów – nie wiem. Co najmniej dwa”.
Dokładnie dwa 🙂
Problem wypełnienia płaszczyzny figurami o różnych kształtach jest pochodzenia, jeśli nie antycznego, to co najmniej średniowiecznego.
Nie znalazłem jednak przypadku analizy dla eLek złożonych z czterech kwadratów. Są, owszem, w Internecie algorytmy dla „małych” eLek, czyli figur złożonych z trzech kwadratów tworzących kąt prosty, ale taki problem jest bardzo łatwy do ogarnięcia, więc nie jest tu przedmiotem rozważań.
Jest więc nisza, w którą każdy może próbować się wcisnąć. W wiadomości 193766 podałem przykład figury
http://pokazywarka.pl/linka7/
dla której gołym okiem widać, że jest nie-eLkowata, ale… jak to wyliczyć/udowodnić/wykazać?
Przyznam, że problem trochę mnie wessał, lecz po dłuższych przemyśleniach nie mam rokującego konceptu. Być może nie ma rozwiązania analitycznego, a może też istnieje takie, lecz ja go nie widzę. Jest to w stu procentach zgodne z ideą Godla, więc…
Pomysły?
@xswedc
Myślę, że przyda się znajomość odpowiedzi na pytanie, które zadałem w komentarzu numer 193763: „Wypełnienie tak utworzonej planszy jest NIEMOŻLIWE”.
Teraz wystarczy wymyślić, jaką wspólną cechę mają pola wyznaczane rzutami kostek.
Podpowiedź: pomoże w tym szachownica.