Przestawki
Freeman Dyson, wybitny fizyk amerykański, jest bohaterem anegdoty, w której pojawia się następująca łamigłówka:
znajdź liczbę, która po przestawieniu ostatniej cyfry na początek zwiększa się dwukrotnie.
Zadanie zostało zaprezentowane na spotkaniu towarzyskim grona uczonych, którzy oniemieli z wrażenia, gdy Dyson po niespełna 10 sekundach stwierdził, że to proste, a najmniejsza liczba, będąca rozwiązaniem, ma 18 cyfr. I miał rację. Jednak błyskawiczne prawie rozwiązanie nie było przejawem geniuszu, jak początkowo sądzono. Okazało się bowiem, że Dyson po prostu znał tę łamigłówkę.
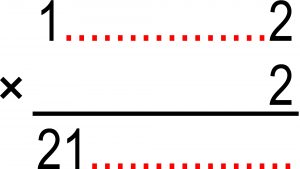
A jest ona rzeczywiście dość prosta. Jeśli przyjąć, ze najmniejsza szukana liczba zaczyna się jedynką, a jej dwukrotność dwójką, to rozwiązanie polega na rozszyfrowaniu poniższego mnożenia, w którym oba rzędy kropek oznaczają ten sam ciąg cyfr.
Zadanie domowe wydaje się trudniejsze, ale czy rzeczywiście takim jest?:
znajdź najmniejszą liczbę, która po przestawieniu przedostatniej cyfry na początek zwiększa się trzykrotnie.

Komentarze
1035 x 3 = 3105
A propos przykładu – to proste! :-)))
Tak na serio, warto zauważyć, że to zadanie ma wiele rozwiązań.
Cyfra jedności szukanej liczby to co najmniej 2, a dla każdej jej dopuszczalnej wartości istnieje odp liczba 18-cyfrowa o szukanej właśnosci:
2x 105263157894736842 = 210526315789473684
2x 157894736842105263 = 315789473684210526
2x 210526315789473684 = 421052631578947368
2x 263157894736842105 = 526315789473684210
2x 315789473684210526 = 631578947368421052
2x 368421052631578947 = 736842105263157894
2x 421052631578947368 = 842105263157894736
2x 473684210526315789 = 947368421052631578
c.d. do przykładu
Jeśli dopuścić 0 jako cyfrę początkową, można dorzucić rozwiązanie z cyfrą jedności =1:
2x 052631578947368421 = 105263157894736842
Co do zadania, przedostatnia cyfra, przestawiana na początek, musi wynosić min. 3, ale dla każdej dopuszczalnej wartości tej cyfry istnieje liczba o szukanej własności (dla 3 najmniejsza):
3x 1035 = 3105
3x 1379310345 = 4137931035
3x 1724137931034482758620689655 = 5172413793103448275862068965
3x 2068965 = 6206895
3x 2413793103448275 = 7241379310344825
3x 27585 = 82755
3x 310344827586206895 = 931034482758620685
Jeśli dopuścić 0 jako cyfrę początkową, można dorzucić rozwiązania z przedostatnią cyfrą 1 i 2:
3x 034482758620689655172415 = 103448275862068965517245
3x 06896551725 = 20689655175
Jedną znalazłam, 28-cyfrową, ale nie wiem, czy jest najmniejsza. Całej nie trzeba chyba podawać.
1724 …. 9655 x 3 = 51724 …. 965
Liczba 28-cyfrowa, mniejsza niż poprzednia:
13793 …. 1724 x 3 = 413793 …. 172
Pani Olu, liczba może być znacznie, znacznie krótsza.
mp
1035×3=3105
3105
Oj. Oczywiście 1035.
Sprawdziłam wszystkie możliwości wg ostatniej cyfry mnożnej (3-9).
Te liczby też mają po 28 cyfr:
1034482758620689655172413793 x 3 =
3103448275862068965517241379
1379310344827586206896551724 x 3 =
4137931034482758620689655172
1724137931034482758620689655 x 3 =
5172413793103448275862068965
20689655172413779310344827586 x 3 =
62068965517241377931034482758
2758620689655172413793103448 x 3 =
8275862068965517241379310344
3103448275862068965517241379 x 3 =
9310344827586206896551724137
Byłam skłonna sądzić, że 28 cyfr to jakaś prawidłowość.
Ale okazało się, że 7 generuje 30 cyfr:
241379310334482758620689665517 x 3 =
724137931033448275862068966551
Jeśli liczba może być znacznie, znacznie krótsza, to znaczy, że z moją metodą szukania jest coś nie tak. Mnożyłam to pisemnie od końca.
Pani Olu, przepraszam, ale dopiero teraz zauważyłem, ze Pani chyba rozwiązuje inne zadanie. Chodzi o przeniesienie na początek PRZEDostatniej cyfry, a Pani cały czas przenosi ostatnią.
mp
Inne zadanie! No ładnie 🙂 Ale nie szkodzi, było bardzo ciekawe.
A odpowiedź na to właściwe proponuję taką: 1035 x 3 = 3105.
W zadaniu Dysona (mnożnik 2) zawsze wychodzi liczba 18-cyfrowa, bez względu na to, jaka jest ostatnia cyfra mnożnej (sprawdziłam dla wszystkich 3-9). To rzeczywiście wygląda na prawidłowość.
157894736842105263 x 2 = 315789473684210526
210526315789473684 x 2 = 431578947368421052
263157894736842105 x 2 = 526315789473684210
315789473684210526 x 2 = 631578947368421052
368421052631578947 x 2 = 736842105263157894
421052631578947368 x 2 = 842105263157894736
473684210526315789 x 2 = 947368421052631578
Ciekawe, czy istnieje mnożnik, dla którego można znaleźć krótsze liczby.
Istnieje, to mnożnik 4:
102564 x 4 = 410256
128205 x 4 = 512820
153846 x 4 = 615384
179487 x 4 = 717948
205128 x 4 = 820512
230769 x 4 = 923076
Liczba poniżej jest najmniejsza przy założeniu, że ostatnią cyfrą mnożnej jest trzy.
1034482758620689655172413793*3=3103448275862068965517241379
Zadanie jest dość proste, chociaż „namnożyć” to się trzeba.
Mnożąc 3*3 otrzymujemy przedostatnią cyfrę równą 9,
następnie 3*9 otrzymujemy 7 itd. aż do skutku. W ten sam sposób można sprawdzić inne liczby na końcowej pozycji.
Liczba Dysona to:
105263157894736842
*2
210526315789473684
Liczba z zagadki jest znacznie mniejsza: 1035 *3 = 3105