Zakręcone 2010

31 grudnia 2009
Marek Penszko

Nowy rok zacznie się jutro, czyli w piątek. Piątek – zły początek. To pierwszy rok XXI wieku zaczynający się tego dnia.  Dobrze chociaż, że styczeń nie zaczyna się 13-go albo że rok nie jest 2013,  ale nie ma tego dobrego, co by… Proszę policzyć, ile różnych liter występuje w liczebniku (złożonym, głównym) oznaczającym 2010. Wszystkiego najlepszego w nowym pechowym roku :).

Próbowałem znaleźć coś osobliwego, a zwłaszcza krzepiącego w liczbie, która będzie nam towarzyszyć przez najbliższe 12 miesięcy. Błądziłem po różnych numeropediach, ale nic nie znalazłem. 2010 jest wyjątkowo nijakie. Chyba żeby się uprzeć i zbierać ciekawostki bardziej zakręcone.
Matematyk-sympatyk zacząłby od rozłożenia liczby na czynniki pierwsze: 2x3x5x67. Nic szczególnego nie widać, poza tym, że cyfry tworzące czynniki rosną wraz z czynnikami.

Noworoczna liczba wygląda  tak, jakby była zapisana w systemie trójkowym. A gdyby tak było, to jakiej liczbie w systemie dziesiętnym odpowiadałoby 2010?

To dobra okazja do powtórki z przerabiania liczb z jednego systemu na inny, w tym przypadku z dziesiętnego na trójkowy…:

20103= (2*3^3 + 0*3^2 + 1*3^3 + 0*3^4)10 = 5710

…i odwrotnie, czyli powracamy do rzeczywistości – 2010 jest liczbą dziesiętną, a szukamy jej bliźniaczki w systemie trójkowym:

2010 : 3 = 670 i reszta 0, czyli ______0 (zaczynamy pisać liczbę trójkową od końca);
670 : 3 = 223 i reszta 1, czyli _____10;
223 : 3 = 74 i reszta 1, czyli ____110;
74 : 3 = 24 i reszta 2, czyli ___2110;
24 : 3 = 8 i reszta 0, czyli __02110;
8 : 3 = 2 i reszta 2, czyli _202110;
2 : 3 = 0 i reszta 2, czyli 2202110.
A zatem 201010 = 22021103. Rzeczywiście bliźniaczki 🙂 .

Pocieszające, że 2010 ma coś wspólnego z „oczkiem”, które jak wiadomo kojarzy się z wygraną (na przykład w kasynie). Nie tylko dlatego, że 21 „tkwi” w 2010, ale przede wszystkim ze względu na to, że to liczba 21-kątna. Mówiąc obrazowo, wielokąt w kształcie 21-kąta foremnego można wypełnić szczelnie 2010 jednakowymi kółkami – lub kulkami-czekoladkami, gdyby był bombonierką – o odpowiedniej średnicy.

I jeszcze jedna zakręcona ciekawostka.
Dzielimy ciąg liczb naturalnych na grupy złożone z parzystej liczby liczb tak, że w pierwszej grupie są dwie liczby, a w każdej następnej o dwie więcej niż w poprzedniej. Liczby w każdej grupie dodajemy. Powstaje ciąg sum:
3 (1+2), 18 (3 + 4 + 5 + 6), 57 (7 + 8 + 9 + 10 + 11 + 12), 132 (13 + …+ 20), 255 (21 +…+30)… itd. Jaka będzie dziesiąta liczba w tym ciągu? Nietrudno zgadnąć.

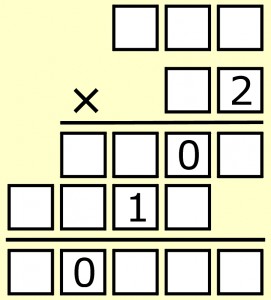
Więcej wyszukanych liczbowych osobliwości noworocznych – w przyszłym roku. A tymczasem proponuję rozszyfrować mnożenie, w którym ujawniła się tylko nasza dobra znajoma, a wraz z nią wszystkie zera występujące w zapisie działania.

W nowym roku życzę Państwu samych „oczek”.