Przepływy
Przed ośmiu laty zamieściłem w Łamiblogu zadanie zainspirowane pierwszym prawem Kirchhoffa. Chodziło o oznaczenie krawędzi grafu skierowanego liczbami od 1 do 13 tak, aby suma liczb „wpływających” do i „wypływających” z każdego węzła (wierzchołka) były równe. Oto znacznie skromniejszy przykład takiego zadania (liczby od 1 do 6, jedna ujawniona):
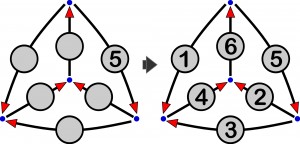
Przykład jest niemal trywialny, ale wraz ze wzrostem liczby krawędzi stopień zawiłości zadania szybko rośnie. Inaczej mówiąc, staje się ono coraz bardziej kombinacyjne. Ponieważ zamieszczone wówczas zadanie pochodziło z mistrzostw świata, więc wywołało dyskusję na temat sensu obecności takich zadań na turniejach. Jeśli bowiem próbowanie i błądzenie zaczyna dominować nad logiką, to zawody z założenia intelektualne zmieniają się w loterię. Istotny jest więc nie tyle rodzaj zadania, co stopień jego komplikacji, który powinien być optymalny, czyli taki, aby w trakcie rozwiązywania logika stanowiła danie główne, a kombinowanie tylko przystawkę lub deser. Co innego natomiast, gdy główkujemy bez współzawodnictwa, dla relaksu. Wówczas nieco większa (ale bez przesady) porcja kombinowania bywa całkiem przyjemna, a poza tym można poszukać jakiejś sprytnej metody, która pozwoli ominąć lub znacznie ograniczyć wyboiste próby, aby w miarę prostą logiczno-rachunkową ścieżką dotrzeć do celu. Być może taką ścieżkę uda się znaleźć w poniższym „przepływowym” zadaniu (w kółkach powinny się pojawić liczby od 1 do 12, trójka już jest), które pochodzi z 24-godzinnych mistrzostw w Budapeszcie. Warto dodać, że z 28 tytanów intelektu i kondycji, startujących w tych mistrzostwach, nie rozwiązał go nikt.
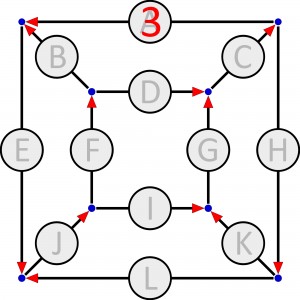
![]()

Komentarze
Rozwiązanie znalezione przez komputer:
a=3, b=5, c=12, d=1, e=8, f=6, g=11, h=9, i=4, j=10, k=7, l=2
A w głowie? 20 minut myślenia nie przyniosło ani rezultatu, ani nawet pomysłu jak się za to zabrać…
Trochę logiki trzeba było użyć – głównie do tego, żeby rozpatrzyć, gdzie może być 1 i 2. Są 4 takie miejsca: B, D, I, L. Potem metodą prób i błędów: B1 – nic z tego; D1 – udało się wszystko dopasować.
A3; B5; C12; D1; E8; F6; G11; H9; I4; J10; K7; L2
Niech mnie kule biją…
Zrobiłem za pierwszym razem, niestety nie ma się czym chwalić, bo to raczej szczęście niż jakieś logiczne myślenie.
http://i.imgur.com/1Vye2MK.png
Ile wynosi prawdopodobieństwo takiego strzału?
A3,B5,C12,D1,E8,F6,G11,H9,I4,J10,K7,L2
W ciągu kilku minut ustaliłem, że 12-ką może być tylko C albo J.
Spróbowałem C12…
… i w pierwszej próbie rozmieściłem całą resztę.
Rozwiązanie to:
A=3,
B=5,
C=12,
D=1,
E=8,
F=6,
G=11,
H=9,
I=4,
J=10,
K=7,
L=2,
Jeśli ktoś jest zainteresowany to kod programu znajdzie na
https://github.com/Jacwing/Przeplywy
@kroQ
Zależy gdzie się strzela. Np. jakie jest prawdopodobieństwo, że strzelając w powietrze na wiwat, strzelę sobie w stopę? (odpowiedź niżej)
B = E-3 = F-D
C = 3+H = D+G
D = F-B = C-G
E = 3+B = J-L
F = B+D = J-I
G = I+K = C-D
H = K+L = C-3
I = G-K = J-F
J = E+L = F+I
K = G-I = H-L
L = J-E = H-K
B+C = J+K = F+G = E+H
D+I = 3+L = C-K = J-B
F-E = D-3 = H-G = L-I
M. (wieloma) in. takie mamy układy równań. Po analizie można ograniczyć np. ostatnie do:
F-E = D-3 = H-G = L-I = {-2; -1; 1; 2; 3; 4}
(a to dlatego, że G,I,K!=3, G=I+K>=5, H=C-3<=9, z czego wynika: H-G <= 5)
Do sprawdzenia jest 6 możliwości i chyba przy każdej "dosyć" szybko da się dojść do sprzeczności lub końcowego rozwiązania.
Wracając do pytania o prawdopodobieństwa: jeśli ktoś mi każe wybrać "losowo", którąś wartość z mojego zbioru, to na pewno nie wezmę pierwszej z brzegu. Wówczas P(x=-2) = 0.
Jeśli natomiast do zadania zabiorę się systematycznie, P(x=-2) = 1.
Tyle teoria. W praktyce zacząłem systematycznie, wybrałem -2 i doszedłem do sprzeczności. Później zacząłem wybierać chaotycznie kolejne wartości i również dostałem sprzeczności. Wreszcie się zniechęciłem i wysmażyłem algorytm, który zrobił wszystko za mnie. Okazało się, że powinienem wybrać -2 i do żadnej sprzeczności nie dochodzić. Niestety u mnie prawdopodobieństwo realizacji takiej powinności jest bliskie zeru.
A=3
B=5
C=12
D=1
E=8
F=6
G=11
H=9
I=4
J=10
K=7
L=2
Posłowie:
Drugą grupę z moich równań można osiągnąć przez przekształcenia pierwszej, ale łatwiej je po prostu odczytać z grafu. Wybieramy dowolny zbiór wierzchołków i sumujemy krawędzie przechodzące z naszego zbioru do pozostałych lub na odwrót (te drugie z minusem). Zresztą w ten sam sposób powstała pierwsza grupa równań – tam zbiorem był pojedynczy wierzchołek. Jeszcze odpowiednio pogrupować wyrazy po obu stronach równań i gotowe. A przy odrobinie wprawy końcowe równania widać na grafie gołym okiem.
A=3, B=5, C=12, D=1, E=8, F=6, G=11, H=9, I=4, J=10, K=7, L=2
A,B,C,…,K,L= 3,5,12,1,8,6,11,9,4,10,7,2.
Można to znaleźć ręcznie w stosunkowo rozsądnym czasie.
Zauważamy, że najlepszymi kandydatami na 12 są C i J.
Ponieważ bliżej A=3 jest C, więc od C zaczniemy próby. Następną dobierana zmienną będzie B. Potem wyliczamy E i H. Teraz musimy próbować kolejne L dla których obliczamy J oraz K. Po czym następna seria prób dla I. Tak więc cały układ ma tylko cztery zmienne niezależne.
W naszej analizie najlepiej (moim zdaniem) jest przyjąć C,B,L,I, właśnie w takiej kolejności. Zaczynamy więc C=12. Wyliczamy H=9. Dla B próbujemy kolejno 1,2,3,4, i otrzymujemy sprzeczności. Dla B=5 mamy E=8 i teraz probujemy L=1 sprzeczność.L=2 to K=7, J=10. Teraz rozwidla się I.
Odrzucamy kolejno I=1,2,3 (bo sprzeczności) i wreszcie I=4 pozwala wyliczyć resztę zmiennych.
Oczywiście relatywna szybkość tej metody opiera się na zaufaniu do autora zadania, że przyjął C=12 a nie np. C=10. 🙂
3 5 12 1 8 6 11 9 4 10 7 2
„Logika” komputera.