Saperska pomyłka

29 lipca 2015
Marek Penszko

Podobno błędy bywają pożyteczne, bo czegoś się na nich uczymy. Oczywiście nie każdy i nie zawsze. W przypadku sapera, który się pomyli, o pożytku nie może być mowy, raczej wręcz przeciwnie. Chyba że błąd będzie dotyczył zadania zwanego saperem. Taka „eksplozja” zdarzyła się w ósmym Omnibusie, na co zwrócili uwagę czytelnicy.

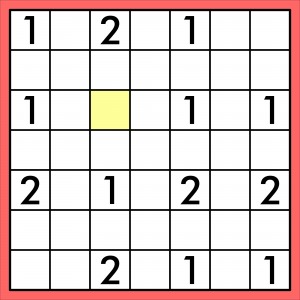
Na stronie 49 jest zestaw sześciu zadań pod tytułem „Mały saper”. Mały, ponieważ diagramy są nieduże (7×7), a ostatni wygląda tak:

Sapp

Z żółtego pola wypadła trójka, więc rozwiązania się rozmnożyły. A pożytek z ubytku taki, że stał się on przyczynkiem do tworzenia innych łamigłówek, jakby wariacji na temat błędu. Z dyskusji z jednym z czytelników wynikły poniższe dwa zadania. Zacznę jednak od przypomnienia zasad „Małego sapera”.

Każda cyfra oznacza, w ilu sąsiednich kratkach – stykających się z polem z cyfrą bokiem lub rogiem – jest mina. Należy oznaczyć wszystkie zaminowane pola, których – to dodatkowy warunek – jest dziesięć.

W pierwszym zadaniu zakładamy, że powyższy diagram (bez trójki) jest poprawny. Natomiast zmieniamy dodatkowy warunek: liczba zaminowanych pól jest najmniejszą możliwą. Jaka jest ta liczba i w których polach są miny?

W drugim, znacznie trudniejszym zadaniu w diagramie cyfry brakuje – ale nie trójki, lecz jedynki. Na którym polu należy umieścić tę jedynkę, aby rozwiązanie było jedno? Wystarczy wskazać jedno takie pole, choć być może ktoś się pokusi o wskazanie wszystkich – jeśli jest ich więcej. Dodatkowy warunek (dziesięć min) pozostaje bez zmian.

Kom