Pokropkowo
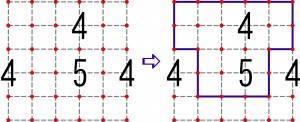
W najnowszym numerze tureckiego kwartalnika Akil oyunlari trafiłem na ciekawą odmianę pokropki. Postanowiłem przedstawić ją w Łamiblogu w formie zagadki indukcyjnej. Oto przykład i jego rozwiązanie – na wszelki wypadek dodam, że jedyne prawidłowe.
Z przykładu proszę wywnioskować, jakie są zasady zabawy, a następnie rozwiązać poniższe zadanie.
W rozwiązaniu wystarczy podać, ile czerwonych kropek otacza linia zamknięta. Dodatkowo warto spróbować zwięźle i jasno przedstawić reguły łamigłówki, co nie jest takie proste.


Komentarze
Myślę, że nie zdradzę reguły, jak powiem, że linia musi być zamknięta, a liczba oznacza ilość kropek należących do linii (wokół tej liczby). Pozostaje jeszcze jedna reguła do odkrycia, ponieważ te dwie generują wiele rozwiązań 🙁
Trzecia reguła to możliwość skrętu tyko na kropkach wokół liczb lub na brzegu planszy.
Moja odpowiedź to 10 kropek.
Odpowiedź dobra, reguła jakby nie.
mp
@Wiąz
Chyba linia nie może się złamać, zanim zakreślone zostaną nią w kolejności 3 kropki – w żadnym małym kwadracie nie mogą być objęte linią wszystkie kropki.
Trochę dobrze.
mp
@Wiąz
Oj, bez sensu wyżej.
Każde dwa odcinki linii ciągłej muszą być oddzielone co najmniej jednym odcinkiem linii przerywanej. Lub – linia w trzech kolejnych punktach nie może skręcić w tę samą stronę.
Nie rozumiem, na czym polega oddzielenie dwu odcinków linii ciągłej jednym odcinkiem przerywanej.
mp
13
_ _
| | _ _ _
| | _ _ | |
|_ |
| _ _ _|
| |
| _ _ _|
Liczba określa liczbę punktów w jej otoczeniu (również po skosie), które są połączone linią. Linia jest łamaną zamkniętą i nie może łamać się w tę samą stronę w trzech kolejnych punktach.
I zagadka:
Na wielkim pustym placu leży rura długości 1 metra i o przekroju 0,5 metra. Na jednym krańcu rury przez jej otwór patrzy biały kot. Na drugim krańcu rury przez jej otwór patrzy czarny kot. Dlaczego te koty się nie widzą*?
*Koty mają dobry wzrok, otwór rury nie jest niczym przesłonięty.
Oj, może to ASCI wyjdzie
__ . . . . .
| . |_ . __
| . . |__| .|
|_ . . . . . |
. |__ . . _|
. . . | . . | .
. . .|___| .
. . . . . . . .
– linia musi być zamknięta
– nie może się przecinać z samą sobą
– dodatkowo musi przechodzić przez dokładnie tyle punktów otaczających daną liczbę ile wskazuje owa liczba
– jeszcze jeden warunek (lub więcej) dotąt mi nie znanych, powyższe natomiast nie dają jednoznacznego rozwiązania zarówno zadania jak i przykładu 🙁
@bubekró:
albo jest ciemna bezksiężycowa noc a plac nie jest oświetlony albo rura nie jest prosta
Może brakującym warunkiem jest to aby obszar będący poza pętlą był spójny?
Wówczas wewnątrz pętli będą tylko trzy czerwone kropki oraz cyfry 5 i 6.
@rubik
Rura jest prosta, a plac jest ciągle oświetlony.
bubekró: więc może to Kot Schrödingera i jest jednocześnie biały i czarny i znajduje się w tym samym czasie po obu końcach rury? 🙂
rubik: to dwa różne koty. No i odpowiedź już chyba znasz.
11
https://www.dropbox.com/s/izn243rfb1al39r/2.png?dl=0
czyli 11. Coś nie tak?
Tak, tzn. nie tak 🙂 Ale może jest reguła inna niż „oficjalna”, która prowadzi do jednoznacznego rozwiązania.
mp
Chyba, że obowiązuje dodatkowa reguła: wielokąt ma obejmować jak najwięcej kropek?
12?
Brakująca reguła: Gospodarz ma zawsze rację 🙂
więc jaka ta reguła?
Cała instrukcja mogłaby brzmieć tak:
„Narysuj linię łamaną zamkniętą, biegnącą po liniach przerywanych i nie przecinającą samej siebie. Linia ta powinna przechodzić przez tyle kropek, otaczających daną liczbę, jaka jest wartość tej liczby. Wszystkie cztery kropki, wyznaczające rogi każdego elementarnego kwadracika siatki, nie mogą znaleźć się na linii
, a jeśli znajdą się dwie lub trzy, to muszą być kolejnymi na linii.”mp
„Wszystkie cztery kropki, wyznaczające rogi każdego elementarnego kwadracika siatki, nie mogą znaleźć się na linii, a jeśli znajdą się dwie lub trzy, to muszą być kolejnymi na linii.”
A nie prościej napisać, że wszystkie kropki elementarnego kwadracika będące na linii, maksymalnie 3, muszą być połączone bezpośrednio ze sobą.
… jak chciałem to napisać, to wydawało mi się to prostsze niż po napisaniu…
@ mp
Bardzo dobra instrukcja. Trzeba tylko usunąć fragment ostatniego zdania – „…, a jeśli znajdą się dwie lub trzy, to muszą być kolejnymi na linii.” -, bo jest ono niepotrzebne.
Bardzo trafna uwaga. Wskazany fragment w przypadku zamieszczonego przykładu i zadania istotnie nie jest potrzebny.
mp
A czy dodatkowa reguła wymagająca by obszar poza linią był spójny także nie powoduje, że rozwiązanie podane w przykładzie jest jednoznaczne?
Wtedy moim zdaniem będzie 5 czerwonych kropek otoczonych linią ciągłą…
W przykładzie ta reguła „działa”, w zadaniu już nie.
mp