Nowinka

10 października 2009
Marek Penszko

Raz na 2-3 miesiące bawię się w „prasówkę”, czyli myszkuję po najciekawszych działach prasy światowej w poszukiwaniu nowości. Prasą są poważne dzienniki, a najciekawszymi działami oczywiście rozrywki umysłowe. Lubię wiedzieć, co w tych działach piszczy, a zwłaszcza czy przypadkiem nie nadciąga następca sudoku. Rozsądek podpowiada, że wystarczyłoby zerkać do gazet brytyjskich oraz że kolejne łamigłówkowe tsunami, jeśli w ogóle nadejdzie, to nie wcześniej niż za ćwierć wieku, o ile do tego czasu prasa nie zniknie. Tym niemniej nawyk myszkowania warto mieć, żeby czegoś ciekawego nie przegapić.

Ostatnio pomieszkuję na Słowacji, więc najbliżej mi do slovenských denníkov. W miarę poważne, czyli ne bulvár, i zasługujące na uwagę są dwa: SME i Pravda (ten tytuł nie za dobrze się kojarzy osobom w moim wieku). Oba są w brytyjskim stylu, czyli sporo miejsca zajmują w nich przeróżne krížovky, hlavolamy i hádanky. Pravda oferuje codziennie aż półtorej kolumny, na której czytelnik może sobie pobazgrać z głową. Obowiązkowo jest sudoku (w SME nawet codziennie dwa), czasem pojawia się kakuro, rzadziej inne zadania z japońskim rodowodem. Wprawdzie w Pravdzie ani w SME na nowinki raczej nie ma co liczyć, ale to, co jest, wygląda na solidną robotę – krzyżówki są ambitne (silnie powiązane wyrazy i niezbyt oklepane), a sudoku wcale nie proste.

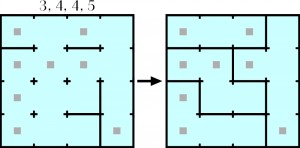
Nowinek, zgodnie z przypuszczeniami, należy jednak szukać przede wszystkim u wyspiarzy. Stało się już niemal regułą, że od czasu do czasu jakiś brytyjski dziennik serwuje nowy drobiazg. Poniżej przykład sprzed paru miesięcy. Nazwy zadania ani miejsca debiutu na razie nie podaję, żeby nikogo nie korciło szukać reguł, które również należy ustalić na podstawie przykładu z rozwiązaniem. Krótko mówiąc, zagadka jest także indukcyjna, jak to już nieraz w Łamiblogu bywało – ostatnio tu i tu i jeszcze tu oraz tu.

A zatem najpierw przykład.

A potem, czyli po rozgryzieniu reguł zabawy – zadanie do rozwiązania.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3 dni.