Król w labiryncie
Autorzy książki Szachy a sztuka negocjacji (Karpow, Phelizon, Kouatly) przyrównują partię szachów do wędrówki w labiryncie. Wykonując ruch na planszy otwieramy jakieś drzwi i wchodzimy do nowego pomieszczenia, w którym dostrzegamy kilka lub kilkanaście następnych drzwi. Pierwszą rzeczą, którą należy wówczas zrobić, jest wskazanie drzwi, które powinny pozostać zamknięte, czyli wybranie dróg, którymi nie należy dalej iść. „Wiedz zawsze zawczasu, czego nie chcesz zrobić” – ta maksyma obowiązuje zarówno w szachach jak i w negocjacjach oraz wszelkich poczynaniach biznesowych. Wędrówki w labiryncie szachowym i poruszanie się w labiryncie rokowań mają zaskakująco wiele wspólnego. Wspomniana książka powinna znaleźć się w spisie lektury obowiązkowej naszych eurodeputowanych (zakładam, że wszyscy oni nieźle grają w szachy).
Przyrównywanie szachów do labiryntu nie jest niczym nowym. Królewska gra tak właśnie traktowana jest w heurystyce, czyli w nauce o twórczym rozwiązywaniu problemów. Ściśle rzecz biorąc, chodzi o problemy „niedookreślone”, czyli takie, w których wybór jakiejś drogi nie gwarantuje, że osiągnie się cel, ale dzięki twórczemu myśleniu można dokonać takiego wyboru, że szansa trafienia w cel będzie zmaksymalizowana. Dla specjalistów od heurystyki, a także dla cybernetyków i kognitywistów szachiści są jak szczury w labiryncie. Jak pracuje ich umysł, gdy dokonują wyboru, którym korytarzem będą dalej podążać i jak stworzyć model takiego arcymistrzowskiego wyszukiwania najlepszych wariantów? – oto zagadki.
Natomiast w całkiem realnym labiryncie szachowym poruszał się 21 lutego br. bułgarski arcymistrz Kirył Georgijew, bijąc w Sofii rekord Guinnessa w najliczniej obsadzonej symultanie. Uczestniczyło w niej 360 osób, trwała ponad 14 godzin; arcymistrz wygrał 280 partii, 74 zremisował, 6 przegrał. Trasa „jednego posunięcia” wynosiła blisko pół kilometra. Kilka dni temu rekord został oficjalnie potwierdzony certyfikatem.
Inną drogę przez labirynt ma przed sobą czarny król na poniższym diagramie. Powinien przedostać się z pola a8 na h1, klucząc między białymi bierkami. Po drodze nie wolno mu oczywiście stawać na szachowanym polu, ale może zbijać bierki – pozostają one nieruchome. Proszę wskazać całą królewską drogę (najkrótszą).


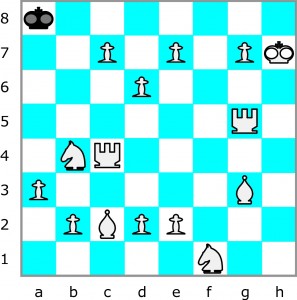

Komentarze
Królewska droga:
Ka8,b7,c8,d7,e6,f6,g5,f6,e6,d7,c8,b7,b6,b5,c4,b5(c5),b6,b7,c8,d7,e6,f6,g5,g4,h3,g2,h1.
Droga ktora znalazlem to : a8-b7-c8-d7-e6-f6-g5(bicie wiezy)-f6-e6-d7-c8-b7-b6-b5-c4(bicie drugiej wiezy)-b5-b6-b7-c8-d7-e6-f6-g5-g4-h3-g2-h1
Razem 27 ruchow. Ciekawe czy to jest najkrotsza, niestety sporo fragmentow sie powtarza(trzeba sie cofac po tej samej drodze ktora sie przyszlo). Mysle to dobre zadanie na wstepny etap olimpiady informatycznej, komputer do takich zabaw nadaje sie niezle.
Pozdrawiam
Wg mnie 22 ruchy. Schemat ze strzałkami poniżej:
http://img41.imageshack.us/img41/3002/szachy.jpg
najpierw czerwony, później niebieski, później zielony. Gdyby się komuś pomyliło 🙂
Czy ta łamigłówka w ogóle ma rozwiązanie? Hetman (Hg5) uniemożliwia królowi przekroczenie piątej linii.
b7,c8,d7,e6,f6,g5,f6,e6,d7,c8,b7,b6,b5,c4,b5,b6,b7,c8,d7,e6,f6,g5,g4,h3,g2,h1
Nie jestem pewien, czy gdzies nie przesadzilem:
b7-c8-d7-e6-f6-g5-f6-e6-d7-c8-b7-b6-b5-c4-b5-b6-b7-c8-d7-e6-f6-g5-g4-h3-g2-h1 = 26 ruchow
(choc ja na miejscu tego krola zamiast ostaniego ruchu zbilbym skoczka, potem piony i gonce za to, ze sie tak musilem nachodzic… raczej „na gore” juz bym nie szedl…)
(jest tez jedna „dwoistosc” -> po biciu na c4 mozna isc albo przez b5 albo przez c5 do pola b6)
W 26 ruchach:
b7, c8, d7, e6, f6, g5, f6, e6, d7, c8, b7, b6, b5, c4, c5(lub b5), b6, b7, c8, d7, e6, f6, g5, g4, h3, g2, h1.
Ale się musi nachodzić, tylko nie wiedzieć po co?
Pozdrawiam
Lepiej niż 24 ruchy chyba się nie da. (do Rafała: Na g5 stoi wieża, a nie hetman)
Gdyby to był Hetman to faktycznie nie dałoby się rozwiązać.
Veromik’u, na d5 konie kopią i tam królowi stawać nie wolno.
Pozdrawiam
Theto, jak zrobic, zeby byly 24 ruchy?
a
A kto powiedział, że w 24 się da? A tak serio, to jakoś przegapiłem, że skoczek jest chroniony i trzeba dwa ruchy nadrobić.