Dookoła koła
W światku łamigłówek matematycznych nie brak prostych zadań, których rozwiązania są z różnych względów zaskakujące i w pierwszej chwili mogą się wydawać błędne. Niektóre z nich mają swoją historię, czy choćby historyjkę.
W roku 1868 pewien czytelnik Scientific American nadesłał do redakcji list z pytaniem: „Ile razy wokół swojej osi obróci się koło przetoczone raz po drugim kole o takiej samej średnicy”? Redakcja opublikowała pytanie i odpowiedź – „raz”. Wywołało to lawinę listów z protestami i wskazaniem, że odpowiedź powinna brzmieć „dwa razy”, a po publikacji kilku z nich – kolejną lawinę od tych, którzy uważali, że jednak powinno być „raz”. Przypominając przed laty tę historię, Martin Gardner zacytował fragment listu jednego ze zwolenników „jednego razu”:
Czy jeśli chwycić kota za ogon i kręcić nim nad głową, to jego głowa i oczy będą się obracać wokół swojej osi? Czy kot zdechnie przy dziewiątym obrocie?
Trudno w to uwierzyć, ale spór toczył się na łamach kilka miesięcy. Niewątpliwie jego przyczyną było nieuwzględnianie… teorii względności :). Kto stoi w okrążanym nieruchomym kole, ten poda inną odpowiedź, niż ten, kto obserwuje cały układ z zewnątrz. Rozwiązujący jest oczywiście poza układem, ale pierwsza możliwość może „mieszać” w głowie.
Uogólnimy nieco problem sprzed lat.
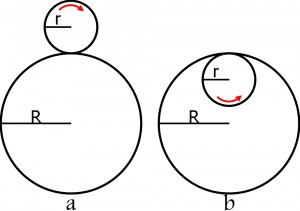
Ile razy wokół swojej osi obróci się małe koło o promieniu r przetoczone raz po obwodzie dużego koła o promieniu R:
a) na zewnątrz koła?
b) wewnątrz koła?
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co kilka dni.

Komentarze
po krótkiej analizie bez użycia kartki i ołówka:
a) R/r razy
b) R/r razy
Źle, ale nie uwalniam, bo jest zbyt blisko celu
mp
no tak, prawidłowa odpowiedź to
a) R/r+1
b) R/r-1
„widać” to gdy wyobrazimy sobie duże kółko jako prostą, którą następnie zawijamy w okrąg.
a) R/r+1
b) R/r-1
Czy ktoś myśli, że jest jakakolwiek różnica w ilości obrotów wewnątrz i na zewnątrz?!
🙂 Jakos nie jestem w stanie wyobrazić sobie by jakakolwiek różnica była między ilością obrotów w przypadku a) i b). Jedyna różnica to to, że koło obraca sie w przeciwną stronę, droga nadal jest tej samej długości, a ilość obrotów będzie funkcją ilorazu obwodów.
… chyba sie pospieszyłem z wnioskami… obracając kółka w głowie wyszło mi, że może być czterokrotnie mniej obrotów wewnątrz niż na zewnątrz…
… dwukrotnie…
Wiązie, liczne komentarze miła rzecz, ale jednak…
Czy jest odpowiednik „głośnego myślenia” dotyczący pisania? 🙂
Każda wielokrotność może być dobra – zależy od promieni kół.
mp
Z pokorą przyjmuję reprymendę 🙂
🙂 mp
W pierwszej chwili także pomyślałem, że nie ma żadnej różnicy pomiędzy obrotami na zewnątrz i wewnątrz… nawet miałem już napisany komentarz… Ale intuicja mi podpowiadała, że jak jest takie proste, to znaczy, że gdzieś jest haczyk. I wychodzi na to, że droga do pokonania taka sama, ale wysiłek inny 😉
Liczba obrotów małego koła ‚r’ wewnątrz dużego ‚R’:
n=R/r -1
na zewnątrz:
n=2*(R/r -1)
Daje to iloraz liczby ‚zewnętrznej’ i ‚wewnętrznej’ równy 2.
🙂 Po głębszym namyśle, w drodze do domu, odkryłem inny wzór:
a) n=R/r * (1+r/R)
b) n=R/r * (1-r/R)
a/b) n=(R+r)/(R-r)
Na zewnatrz – R/r +1
Wewnatrz – R/r – 1
a
1) R/r+1
2) (R/r+1)/2
Na zewnątrz małe koło pokonuje drogę 2*pi*R+2*pi*r (bo się obraca) to należy podzielić przez 2*pi*r. Czyli jeżeli koła są równe to koło zewnętrzne obróci się dwa razy, przebywając drogę wokół nieruchomego koła. Wewnątrz zakładamy r=R. Aby punkt ruchomego okręgu przesunął się po nieruchomym okręgu wystarczy jeden obrót, czyli stosunek drogi zewnętrznej do wewnętrznej jest jak 2:1.
Gdyby obwód dużego koła narysować jako linie prostą to małe koło wykonałoby dokładnie R/r obrotów, a ponieważ obwód jest zwinięty (droga po której porusza się mniejsze koło jest kołem) to mniejsze koło poruszając się po takiej drodze i wykonując… nie wiem jak to nazwać… ruch postępowy obrotowy względem swego środka, wykona dodatkowy obrót. Natomiast wykonując ruch wewnątrz, mniejsze koło obraca się jakby przeciwnie do ruchu swego środka i w ten sposób koło ‚zgubi’ jeden obrót. Podsumowując, mniejsze koło po linii prostej o długości równej obwodowi dużego koła wykona R/r obrotów, po drodze kolistej, na zewnątrz dużego koła wykona o jeden więcej obrót czyli R/r+1, a wewnątrz koła o jeden mniej niż po linii prostej czyli R/r-1
Pięknie! Od razu trzeba było tak pisać 🙂
mp
a: R/r + 1
b: R/r – 1
Poniekąd pokrewne jest pytanie z astronomii: ile czasu trwa obrót Ziemi wokół własnej osi (albo ile takich obrotów zachodzi w ciągu roku).
R/r dla sytuacji (a) i (b).
Jeżeli rozwiniemy okręgi to od razu widać, że niema znaczenia czy obracane koło jest w środku czy na zewnątrz. Długości okręgów się nie zmienią.
Obracane koło w (a) jak i w (b) zawsze styka się jednym punktem z kołem o promieniu R i związku z tym nie pokonuje jakiejś dodatkowej drogi.
Czy w tym rozumowaniu jest jakiś błąd?
Koła toczą się po obwodzie w tym samym kierunku, ale obracają się w przeciwne strony. Stąd różnica we wzorach.
mp
„Koła toczą się po obwodzie w tym samym kierunku, ale obracają się w przeciwne strony. Stąd różnica we wzorach. mp” – jakoś nie rozumiem i
intuicja mnie całkowicie zawodzi.
Analitycznie to będzie tak:
(a)
Środek obracanego koła porusza się po promieniu R+r.
Obwód drogi poruszającego się koła koła to 2*pi*(R+r).
A teraz równie: 2*pi*(R+r) = 2*pi*r*x
x = (R+r)/r = R/r + 1
(b)
Środek obracanego koła porusza się po promieniu R-r.
Obwód drogi poruszającego się koła koła to 2*pi*(R-r).
A teraz równie: 2*pi*(R-r) = 2*pi*r*x
x = (R-r)/r = R/r – 1