Pasjansik
Zdrobniale, bo potrzeba tylko 10 kart, a zabawa trwa najwyżej minutę.
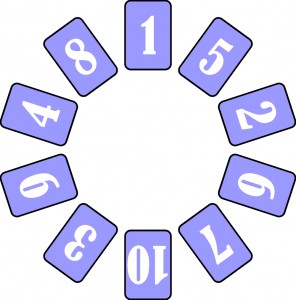
Występują: as, który pełni rolę jedynki, blotki (od 2 do 9) oraz dziesiątka. Wszystkie te karty układamy odkryte w kształcie okręgu – w przypadkowej kolejności. Karciane kółko może więc w wersji liczbowej wyglądać na przykład tak:
Zaczynamy od dowolnej karty i wykonujemy kolejno 10 ruchów. Każdy składa się z dwóch etapów i polega na:
– odwróceniu wybranej karty liczbą do dołu,
– odliczeniu w kierunku zgodnym z ruchem wskazówek zegara, zaczynając od następnej karty, tylu kart, jaka liczba była na odwróconej.
Od karty, na której zakończymy liczenie, wykonywany jest następny ruch, czyli jej odwrócenie, a potem wyliczanka itd. Pasjans wyjdzie, jeżeli odwrócimy wszystkie karty w 10 ruchach, a właściwie w 10 i pół, bo odwrócenie dziesiątej będzie połową jedenastego ruchu.
Dla układu przedstawionego na rysunku wróżba związana z pasjansem nie wypadnie niestety pomyślnie. Od którejkolwiek karty byśmy nie zaczęli, wszystkich nie odwrócimy. Najbliżej celu będziemy startując od czwórki. Wówczas kolejno „zniknie” 7 cyfr: 4, 2, 7, 5, 3, 8, 9, a ostatnia wyliczanka zakończy się na koszulce trójki.
Pasjansik można stawiać, ale ponieważ nie jest zbyt wyszukany, więc nadaje się raczej do rozwiązywania. Bardzo łatwo zauważyć, że nie ma sensu zaczynać od dziesiątki oraz że wypadałoby na dziesiątce zakończyć, jeśli pasjans ma wyjść. Proszę spróbować samemu wyciągnąć inne wnioski dotyczące układu liczb i znaleźć układ, przy którym pasjans wychodzi – oczywiście po rozpoczęciu od odpowiedniej liczby. Nie jest to łatwe, choć takich układów jest dużo – 288, jeśli komputer się nie pomylił.

Komentarze
9 7 5 3 1 10 8 6 4 2
Nie było chyba trudne, najpierw malejąco nieparzyste, później malejąco parzyste i jest OK.
Metoda sprawdza się, gdy zamiast liczby 10 weźmiemy dowolną liczbę parzystą.
A co z nieparzystą liczbą N?
Pazdrawiam
Z nieparzystą liczbą N nie jest tak dobrze.
Każda liczba wskazuje ile kroków należy wykonać, aby znaleźć się w następnym polu. Skoro tak, to policzmy ile musimy wykonać wszystkich kroków dla zadanego N i określmy na którym polu zakończymy swoją wędrówkę.
Wszystkich kroków jest 1+2+…+(N-1), czyli N(N-1)/2. Poruszając się po okręgu musimy wykonać pewną liczbę okrążeń. Czyli N(N-1)/2 mod N wskaże nam ostatnie pole względem pola od którego rozpoczeliśmy naszą wędrówkę.
Dla parzystego N wyrażenie N(N-1)/2 mod N jest równe N/2. W przypadku N=10 kończymy na piątym polu licząc od pola początkowego.
Gdy N jest nieparzyste, to wyrażenie N(N-1)/2 mod N jest równe 0. Czyli musielibyśmy zakończyć swoją wędrówkę na polu początkowym. A to jest możliwe jedynie dla N=1.
Pozdrawiam
Też mi wyszło, że jest 288 rozwiązań. Rozpoczynamy zawsze od ostatniej liczby. Aby było czytelniej X (rzymskie) zastępuje 10.
Antyp
1234X56789
1259X34786
1259X34867
1264X58973
1264X59783
1349X52678
1364X89527
1385X26974
1385X27946
1385X29647
1453X78629
1453X86729
1467X28953
1483X26759
1485X27963
1524X86379
1527X39648
1534X86729
1537X28649
1537X92648
1562X78394
1564X89723
1564X97823
1569X28374
1623X74859
1623X84579
1629X34857
1645X89723
1645X97823
1647X92853
1723X59648
1723X84596
1749X28356
1783X29564
2315X64897
2315X64978
2345X67891
2347X61859
2347X69158
2348X51679
2357X69184
2358X14679
2364X85971
2367X15894
2395X14678
2458X37961
2468X91357
2495X17368
2495X81367
2564X89731
2564X97831
2567X91834
2568X91374
2594X37861
2597X31864
2615X94837
2641X57839
2645X89731
2645X97831
2648X39751
2691X34857
2731X64958
2734X68951
2734X85961
2741X69358
2793X51864
2914X35786
2914X35867
2934X85167
2935X17468
2935X81467
2945X81736
2948X31756
3125X64897
3125X64978
3148X52796
3152X64789
3164X58972
3164X59782
3164X95827
3185X29467
3458X16729
3458X72961
3458X96127
3461X75928
3468X91527
3469X25781
3469X51782
3485X16792
3495X26781
3529X64178
3561X79428
3562X78491
3569X28471
3581X26479
3582X61749
3584X79162
3584X96172
3594X72861
3628X14579
3628X59147
3648X92571
3649X58172
3682X15749
3682X95147
3691X52847
3728X14596
3741X69528
3742X68591
3752X68941
3781X25946
3791X24586
3925X16478
3925X61847
3941X62578
3951X62847
3964X18572
4137X25689
4138X52697
4152X67389
4183X25679
4185X27936
4185X29637
4237X61589
4257X69183
4267X15893
4283X61579
4295X71386
4297X31586
4518X72396
4582X71639
4589X27136
4618X52973
4639X57182
4683X79152
4692X57183
4695X17823
4697X12853
4713X69528
4739X15628
4739X51682
4792X51683
4793X81526
4913X62578
4938X26157
4952X67183
5124X67389
5128X34697
5164X97382
5261X74938
5263X78491
5264X78931
5267X18493
5267X91483
5281X36497
5283X61749
5289X31467
5294X36781
5317X26489
5317X62948
5348X71629
5348X72691
5397X12648
5397X26184
5618X92347
5648X97123
5649X82731
5689X12734
5691X82347
5693X82741
5714X96382
5728X16394
5748X91623
5791X24683
5913X72468
5914X36782
5928X31647
5948X27163
6124X85379
6134X85729
6138X52794
6157X92834
6158X92374
6184X39752
6185X29734
6284X95173
6285X91473
6294X58173
6359X82471
6382X71459
6394X72851
6394X82571
6395X71824
6415X78392
6417X28539
6417X38592
6417X92538
6418X52793
6427X81539
6428X37591
6429X57138
6458X97123
6459X82731
6481X27539
6481X37592
6489X31752
6491X37528
6495X81723
6497X28153
6712X95348
6738X91524
6751X89342
6751X89423
6781X29453
6782X91453
6915X28473
6925X71834
6951X82473
6952X78134
7123X64859
7138X52964
7163X94852
7163X95824
7231X56489
7231X64589
7235X96481
7249X58136
7261X59483
7281X35946
7291X34586
7293X58146
7312X56489
7312X64589
7318X52946
7369X15824
7382X15649
7382X16459
7389X12456
7392X56184
7395X16824
7418X52963
7461X85923
7493X82561
7528X39641
7531X86429
7538X92641
7561X89423
7581X39642
7592X38641
7923X85146
7925X16834
7935X18642
7938X12564
8152X94637
8153X94672
8231X56497
8231X64597
8239X51467
8249X51736
8251X64973
8251X74936
8259X14736
8293X51746
8312X56497
8312X64597
8342X67591
8342X75691
8349X25671
8352X67941
8392X51647
8423X75691
8459X17362
8491X26357
8493X26751
8512X64793
8514X79362
8514X96372
8537X91642
8591X24673
8591X27346
8592X71364
8612X94537
8612X95347
8613X94572
8642X97531
8931X25647
8931X26457
8941X25673
Dla mnie zadanie było trudne tylko do chwili, kiedy zobaczyłem rozwiązanie podane przez Jazza. Potem było już łatwo.
Dla nieparzystego N=1 pasjans wychodzi.
Jazzie, przyjemnie poczytac Twoje wyjasnienia dotyczace nieparzystej liczby kart. Sa jak trafienie w dziesiatke.
a
Andy, dziękuję, czasem się uda.
Pozdrawiam