Rządy hetmanów
Problem ośmiu hetmanów, o którym wspomniałem poprzednio, jest najbardziej znanym zadaniem matematyczno-szachowym. Popularność zawdzięcza między innymi temu, że zajmowały się nim takie tuzy jak Gauss i Cantor. Nieco mniej znane, choć bardziej wiekowe, jest tzw. zagadnienie dominacji hetmanów, wywodzące się z podstępnej XVII-wiecznej łamigłówki nie tylko dla szachistów.
Na szachownicy należy rozstawić 4 hetmany tak, aby wszystkie wolne pola były atakowane.
Próbowano wielokrotnie, długo, wytrwale i bezskutecznie. Rozwiązanie nie istnieje – zawsze co najmniej dwa pola pozostają nieatakowane. Próby trwały, bo nie tak łatwo dowieść, że to niemożliwe.
Pod koniec XIX wieku problem uogólnili i wzięli pod lupę matematycy.
Ile co najmniej hetmanów należy umieścić na planszy n x n, aby każde wolne pole było atakowane przez przynajmniej jednego z nich?
Zagadnienie okazało się wyzwaniem. Chociaż w ostatnich latach dzięki wsparciu komputerowemu znaleziono rozwiązania nawet dla monstrualnych plansz, to z podporządkowaniem wyników jakimś regułom jest kłopot. Chaos panuje mniej więcej taki, jak w ciągu liczb pierwszych, a wiele problemów pozostaje nierozstrzygniętych. Na najprostszym przykładzie można pokazać, jak to się plecie.
Dla planszy 3 x 3 hetman ustawiony w centrum załatwia sprawę. Dodajemy wiersz i kolumnę, dostawiamy w rogu hetmana i też jest OK. Potem pojawia się następny skrajny wiersz i kolumna plus hetman w rogu i nadal jest w porządku, bo planszy 5 x 5 mniej niż trzy hetmany nie opanują.
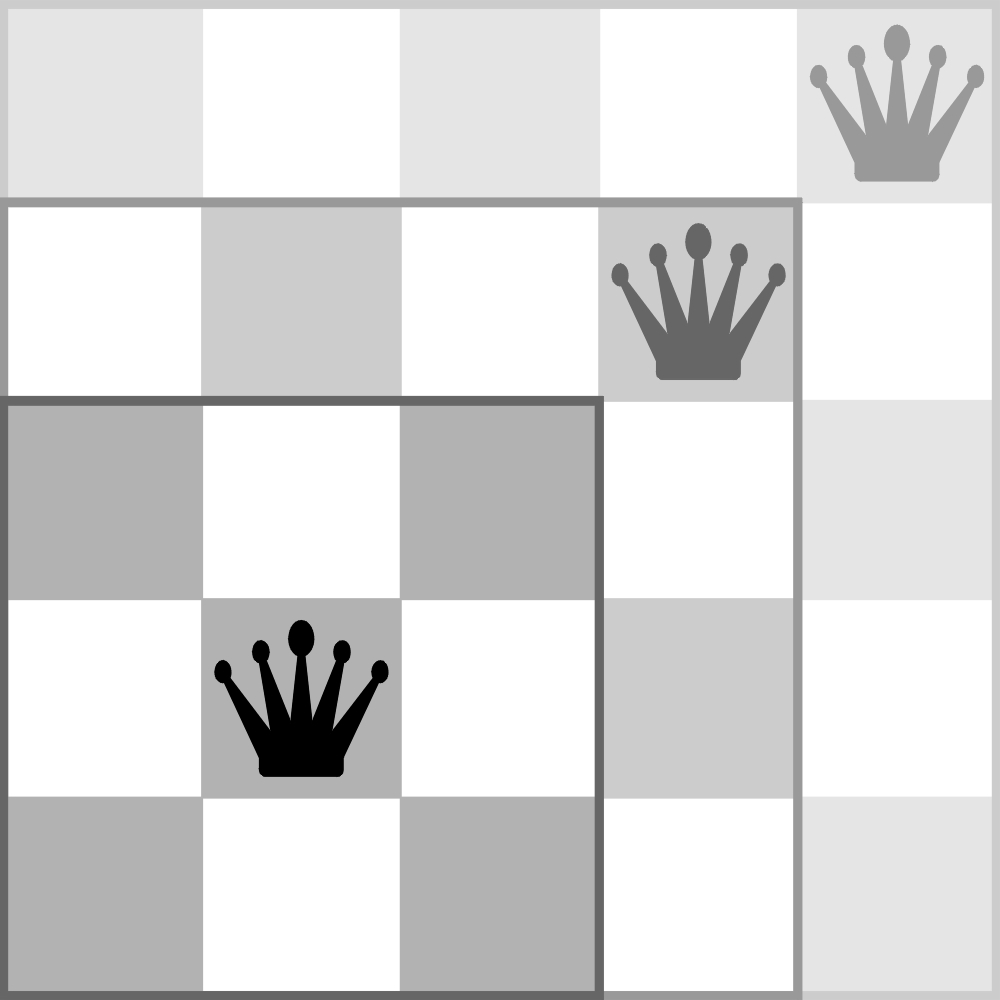
Moglibyśmy tak w nieskończoność dodawać dwa rzędy i hetmana, gdyby nie to, że już przy planszy 6 x 6 przekroczymy normę. Nowego hetmana dostawiać nie trzeba – trzy wystarczą, jeśli w rozwiązaniu dla 5 x 5, umieszczonym na 6 x 6, wykonamy trzy ruchy:
Dla planszy 7 x 7 i 8 x 8 postępujemy zgodnie z początkowym schematem i docieramy do 9 x 9 z następującym układem (przeniesionym z 8 x 8):
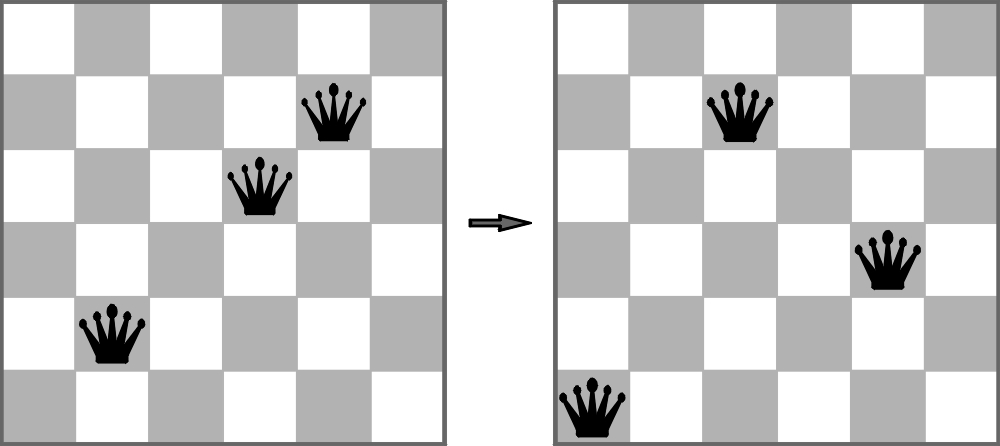
Teraz także nie trzeba dostawiać hetmana. Wystarczy niektóre z obecnych odpowiednio przesunąć – zgodnie z zasadami ich poruszania się – aby wszystkie wolne pola planszy 9×9 były atakowane. Iloma co najmniej hetmanami należy wykonać po jednym ruchu i w jaki sposób?
Co ciekawe, poczynając od 9 x 9 pojawia się nowy sposób rozmieszczania hetmanów, znacznie bardziej efektywny. Dzięki niemu do opanowania pola 11 x 11 także dość będzie pięciu hetmanów. Może się to wydać nieprawdopodobne, skoro z obszarem prawie dwukrotnie mniejszym cztery nie dawały sobie rady.


Komentarze
1. a1-e5
2. c5-c8
3. e3-b3
4. g7-g2
5. h8-h7
Znalazłem rozwiązanie najgorsze z możliwych (pięć posunięć), co nie oznacza, że istnieje lepsze.
Wystarczy przesunąć trzy hetmany:
1.c5-c7
2.g7-i9
3.h8-g9
I jest to jedyne możliwe rozwiązanie.
Do Antypa:
Rozwiązanie jest prima…aprilisowe?
Bo dwa pola h4 i h5 nie sa atakowane.
a
Błąd jest niezamierzony. Powinno być tak
1.c5-c7
2.g7-i5
3.h8-g8
Antypie, teraz jest wyłącznie prima… Gratuluję!
mp