Trójki przyrożne
Pisałem niedawno, że dowodów nie będzie. Uściślę: nie będzie zbyt trudnych lub zawiłych dowodów. Natomiast proste dowodziki mogą się okazjonalnie i w rolach drugoplanowych pojawiać. Jak na przykład w tym wpisie.
Dysponujemy trzynastoma różnymi liczbami całkowitymi – od 1 do 13. Dwunastoma z nich oznaczamy krawędzie sześcianu w taki sposób, że
suma liczb na trzech krawędziach zbiegających się przy każdym wierzchołku jest taka sama.
Nazwijmy te trójki liczb przyrożnymi.
Oto cztery stwierdzenia dotyczące tego osobliwego układu liczb na krawędziach:
1. jedną trójkę przyrożną tworzą trzy kolejne wyrazy postępu arytmetycznego.
2. dwie trójki przyrożne składają się wyłącznie z liczb nieparzystych.
3. wśród liczb na krawędziach nie ma trzynastki.
4. jedna trójka przyrożna to trzy potęgi.
Niestety, prawdziwość powyższych stwierdzeń budzi wątpliwości. Które z nich na pewno są fałszywe?
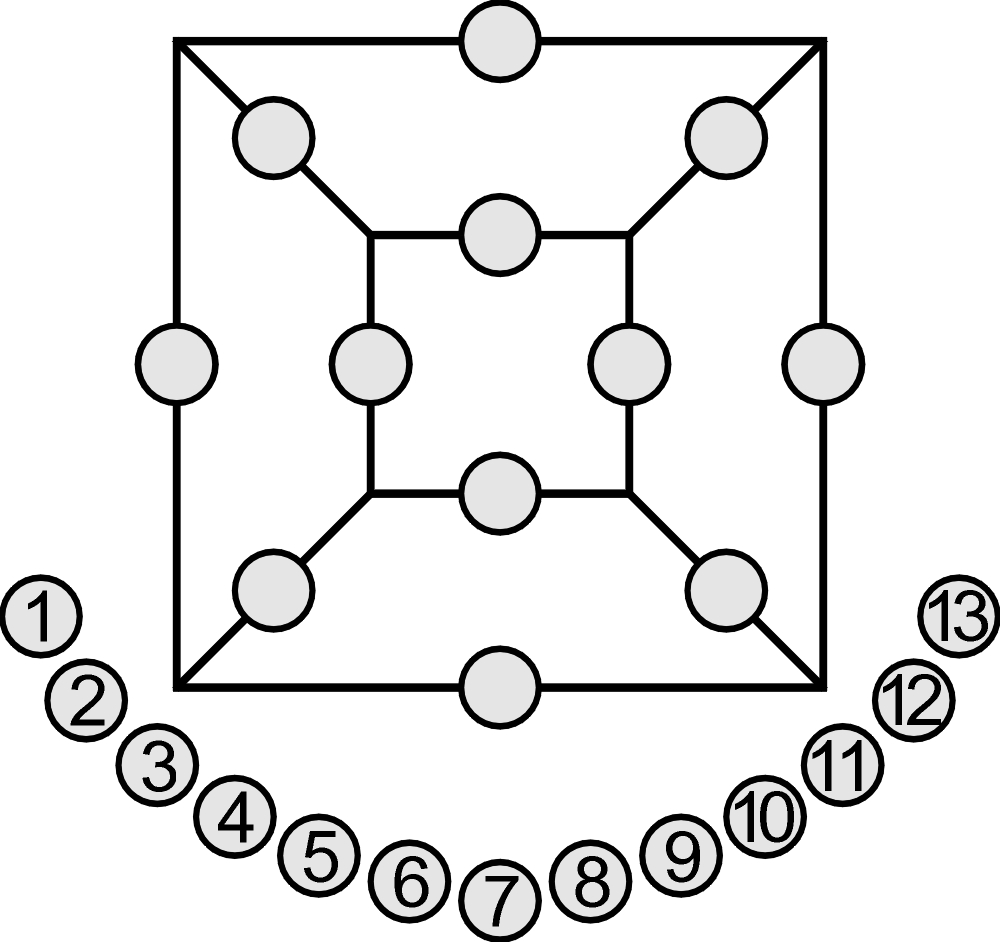
I zadanie dodatkowe: proszę podać przykład takiego rozmieszczenia liczb na poniższym schemacie sześcianu, które będzie zgodne przynajmniej z jednym z podanych stwierdzeń.

Komentarze
Ułożenie liczb zgodne z podstawowym warunkiem zadania, „suma liczb na trzech krawędziach zbiegających się przy każdym wierzchołku jest taka sama” , jest możliwe tylko w przypadku, jeżeli wybierzemy takie liczby, których podwojona suma jest podzielna przez 8. Ponieważ suma liczb od 1 do 13 jest równa 91, to możemy wyrzucić tylko liczby 3, 7 lub 11. Wówczas sumy przy wierzchołkach będą równe odpowiednio 22, 21 lub 20.
1.Mamy sumę ciągu arytmetycznego a+(a+n)+(a+2n)=S. Po przekształceniu 3a+3n=S. Widać, że S=21 bo jest jedyna liczba podzielna przez 3. Więc a+n=7, czyli środkowy wyraz ciągu jest równy 7, ale 7 jest wyrzucone. Więc nie ma takiego układu liczb, który by spełniał ten warunek.
2.Ten warunek też może być spełniony tylko w przypadku gdy S=21 np. 1,9,11, ponieważ 21 możemy otrzymać jako sumę 3 liczb nieparzystych lub dwóch parzystych i jednej nieparzystej. Sum jest 8, liczb 24 (bo każdą używamy dwukrotnie) 12 parzystych i 12 nieparzystych, więc jest 6 układów parzysto-nieparzystych (dwie liczby parzyste i jedna nieparzysta) i dwa nieparzyste (składających się wyłącznie z licz nieparzystych).
3. W każdym zbiorze liczb, które można ustawić zgodnie z warunkami zadania jest trzynastka więc zawsze na jednej z krawędzi musi być trzynastka.
4. Potęgami, które można użyć są 1,4,8,9. Trzy liczby to 4+8+9=21, trzeba to sprawdzić. Po sprawdzeniu jestem prawie pewny, że nie ma takiego układu.
Na pewno fałszywe są stwierdzenia 1 i 3, prawdopodobnie prawdziwe 2 (trzeba ułożyć odpowiedni układ). Wszystkie możliwe układy poniżej, liczby wpisujemy po kolei w kółka od góry do dołu, na końcu jest suma.
Nie wyrzucałem układów, które powstają przez symetrię, obrót itd.
1 6 7 4 13 10 9 12 2 8 3 5 20
1 6 10 2 13 12 8 9 3 5 7 4 20
1 7 6 4 12 9 10 13 3 8 2 5 20
1 7 9 8 12 5 3 10 2 13 4 6 20
1 9 7 8 10 3 5 12 4 13 2 6 20
1 9 13 4 10 7 3 6 8 5 12 2 20
1 10 6 2 9 8 12 13 7 5 3 4 20
1 10 12 6 9 4 2 7 3 13 5 8 20
1 12 10 6 7 2 4 9 5 13 3 8 20
1 12 13 5 7 3 2 6 9 8 10 4 20
1 13 9 4 6 3 7 10 12 5 8 2 20
1 13 12 5 6 2 3 7 10 8 9 4 20
2 5 8 3 13 12 9 10 1 7 4 6 20
2 5 12 7 13 8 1 6 3 9 10 4 20
2 6 10 1 12 13 9 8 3 4 7 5 20
2 6 13 4 12 10 3 5 1 9 8 7 20
2 8 5 3 10 9 12 13 4 7 1 6 20
2 8 12 5 10 7 3 6 9 4 13 1 20
2 10 6 1 8 9 13 12 7 4 3 5 20
2 10 13 6 8 4 1 5 9 7 12 3 20
2 12 5 7 6 1 8 13 10 9 3 4 20
2 12 8 5 6 3 7 10 13 4 9 1 20
2 13 6 4 5 3 10 12 8 9 1 7 20
2 13 10 6 5 1 4 8 12 7 9 3 20
3 4 5 7 13 9 8 12 1 10 2 6 20
3 4 9 10 13 6 1 8 2 12 7 5 20
3 5 4 7 12 8 9 13 2 10 1 6 20
3 5 8 2 12 13 10 9 1 6 4 7 20
3 8 5 2 9 10 13 12 4 6 1 7 20
3 8 13 5 9 7 2 4 1 12 6 10 20
3 9 4 10 8 1 6 13 7 12 2 5 20
3 9 12 7 8 4 1 5 10 6 13 2 20
3 12 9 7 5 1 4 8 13 6 10 2 20
3 12 13 6 5 2 1 4 8 10 9 7 20
3 13 8 5 4 2 7 9 6 12 1 10 20
3 13 12 6 4 1 2 5 9 10 8 7 20
4 3 7 5 13 12 8 9 6 2 10 1 20
4 3 10 9 13 8 1 6 5 7 12 2 20
4 6 7 1 10 13 12 9 2 5 3 8 20
4 6 13 2 10 12 5 3 1 7 8 9 20
4 7 3 5 9 8 12 13 10 2 6 1 20
4 7 6 1 9 12 13 10 3 5 2 8 20
4 9 10 8 7 3 2 6 12 5 13 1 20
4 9 13 1 7 10 6 3 8 2 12 5 20
4 10 3 9 6 1 8 13 12 7 5 2 20
4 10 9 8 6 2 3 7 13 5 12 1 20
4 13 6 2 3 5 12 10 8 7 1 9 20
4 13 9 1 3 6 10 7 12 2 8 5 20
5 2 3 8 13 10 9 12 6 4 7 1 20
5 2 7 12 13 6 1 8 4 10 9 3 20
5 3 2 8 12 9 10 13 7 4 6 1 20
5 3 7 4 12 13 9 8 6 1 10 2 20
5 7 2 12 8 1 6 13 9 10 4 3 20
5 7 3 4 8 9 13 12 10 1 6 2 20
5 8 12 2 7 10 6 3 9 1 13 4 20
5 8 13 3 7 9 4 2 1 10 6 12 20
5 12 8 2 3 6 10 7 13 1 9 4 20
5 12 13 1 3 7 6 2 9 4 10 8 20
5 13 8 3 2 4 9 7 6 10 1 12 20
5 13 12 1 2 6 7 3 10 4 9 8 20
6 1 2 10 13 9 8 12 4 7 5 3 20
6 1 4 7 13 12 9 10 5 3 8 2 20
6 2 1 10 12 8 9 13 5 7 4 3 20
6 2 4 13 12 5 3 10 7 8 9 1 20
6 4 1 7 10 9 12 13 8 3 5 2 20
6 4 2 13 10 3 5 12 9 8 7 1 20
6 10 12 1 4 9 7 2 3 8 5 13 20
6 10 13 2 4 8 5 1 9 3 12 7 20
6 12 10 1 2 7 9 4 5 8 3 13 20
6 12 13 3 2 5 4 1 8 7 9 10 20
6 13 10 2 1 5 8 4 12 3 9 7 20
6 13 12 3 1 4 5 2 9 7 8 10 20
7 1 4 6 12 13 10 9 5 2 8 3 20
7 1 8 9 12 10 3 5 6 4 13 2 20
7 4 1 6 9 10 13 12 8 2 5 3 20
7 4 5 3 9 13 12 8 1 6 2 10 20
7 5 4 3 8 12 13 9 2 6 1 10 20
7 5 12 2 8 13 6 1 3 4 10 9 20
7 8 1 9 5 3 10 12 13 4 6 2 20
7 8 9 10 5 2 1 4 12 6 13 3 20
7 9 8 10 4 1 2 5 13 6 12 3 20
7 9 12 3 4 8 5 1 10 2 13 6 20
7 12 5 2 1 6 13 8 10 4 3 9 20
7 12 9 3 1 5 8 4 13 2 10 6 20
8 2 3 5 10 13 12 9 6 1 7 4 20
8 2 5 12 10 6 3 7 1 13 4 9 20
8 3 2 5 9 12 13 10 7 1 6 4 20
8 3 5 13 9 4 2 7 10 6 12 1 20
8 5 2 12 7 3 6 10 4 13 1 9 20
8 5 3 13 7 2 4 9 12 6 10 1 20
8 7 9 1 5 12 10 3 2 6 4 13 20
8 7 10 9 5 4 1 2 3 13 6 12 20
8 9 7 1 3 10 12 5 4 6 2 13 20
8 9 10 4 3 7 6 2 12 1 13 5 20
8 10 7 9 2 1 4 5 6 13 3 12 20
8 10 9 4 2 6 7 3 13 1 12 5 20
9 1 4 13 10 6 3 7 2 12 5 8 20
9 1 8 7 10 12 5 3 6 2 13 4 20
9 3 7 12 8 5 1 4 2 13 6 10 20
9 3 10 4 8 13 6 1 5 2 12 7 20
9 4 1 13 7 3 6 10 5 12 2 8 20
9 4 8 10 7 6 2 3 1 13 5 12 20
9 7 3 12 4 1 5 8 6 13 2 10 20
9 7 10 8 4 5 2 1 3 12 6 13 20
9 8 1 7 3 5 12 10 13 2 6 4 20
9 8 4 10 3 2 6 7 5 13 1 12 20
9 10 3 4 1 6 13 8 12 2 5 7 20
9 10 7 8 1 2 5 4 6 12 3 13 20
10 1 2 6 9 13 12 8 4 3 5 7 20
10 1 6 12 9 7 2 4 8 5 13 3 20
10 2 1 6 8 12 13 9 5 3 4 7 20
10 2 6 13 8 5 1 4 3 12 7 9 20
10 4 8 9 6 7 3 2 1 12 5 13 20
10 4 9 3 6 13 8 1 2 5 7 12 20
10 6 1 12 4 2 7 9 13 5 8 3 20
10 6 2 13 4 1 5 8 7 12 3 9 20
10 8 4 9 2 3 7 6 5 12 1 13 20
10 8 9 7 2 5 4 1 12 3 13 6 20
10 9 4 3 1 8 13 6 7 5 2 12 20
10 9 8 7 1 4 5 2 13 3 12 6 20
12 1 5 13 7 6 2 3 4 10 8 9 20
12 1 6 10 7 9 4 2 8 3 13 5 20
12 2 5 8 6 10 7 3 1 9 4 13 20
12 2 7 5 6 13 8 1 4 3 9 10 20
12 3 6 13 5 4 1 2 7 9 10 8 20
12 3 7 9 5 8 4 1 2 10 6 13 20
12 5 1 13 3 2 6 7 8 10 4 9 20
12 5 2 8 3 7 10 6 4 9 1 13 20
12 6 1 10 2 4 9 7 13 3 8 5 20
12 6 3 13 2 1 4 5 10 9 7 8 20
12 7 2 5 1 8 13 6 9 3 4 10 20
12 7 3 9 1 4 8 5 6 10 2 13 20
13 1 4 9 6 10 7 3 2 8 5 12 20
13 1 5 12 6 7 3 2 4 9 8 10 20
13 2 4 6 5 12 10 3 7 1 9 8 20
13 2 6 10 5 8 4 1 3 9 7 12 20
13 3 5 8 4 9 7 2 10 1 12 6 20
13 3 6 12 4 5 2 1 7 8 10 9 20
13 4 1 9 3 7 10 6 5 8 2 12 20
13 4 2 6 3 10 12 5 9 1 7 8 20
13 5 1 12 2 3 7 6 8 9 4 10 20
13 5 3 8 2 7 9 4 12 1 10 6 20
13 6 2 10 1 4 8 5 7 9 3 12 20
13 6 3 12 1 2 5 4 10 8 7 9 20
1 8 9 10 12 3 2 11 5 13 6 4 21
1 9 8 10 11 2 3 12 6 13 5 4 21
1 11 12 4 9 6 5 8 2 13 3 10 21
1 12 11 4 8 5 6 9 3 13 2 10 21
2 6 9 11 13 4 1 10 5 12 8 3 21
2 9 6 11 10 1 4 13 8 12 5 3 21
2 10 13 3 9 8 5 6 1 12 4 11 21
2 13 10 3 6 5 8 9 4 12 1 11 21
3 5 8 12 13 4 1 10 6 11 9 2 21
3 8 5 12 10 1 4 13 9 11 6 2 21
3 10 13 2 8 9 6 5 1 11 4 12 21
3 13 10 2 5 6 9 8 4 11 1 12 21
4 5 6 13 12 3 2 11 8 10 9 1 21
4 6 5 13 11 2 3 12 9 10 8 1 21
4 11 12 1 6 9 8 5 2 10 3 13 21
4 12 11 1 5 8 9 6 3 10 2 13 21
5 3 12 8 13 10 1 4 2 9 11 6 21
5 4 13 6 12 11 2 3 1 9 10 8 21
5 12 3 8 4 1 10 13 11 9 2 6 21
5 13 4 6 3 2 11 12 10 9 1 8 21
6 2 11 9 13 10 1 4 3 8 12 5 21
6 4 13 5 11 12 3 2 1 8 10 9 21
6 11 2 9 4 1 10 13 12 8 3 5 21
6 13 4 5 2 3 12 11 10 8 1 9 21
8 1 10 9 12 11 2 3 4 6 13 5 21
8 3 12 5 10 13 4 1 2 6 11 9 21
8 10 1 9 3 2 11 12 13 6 4 5 21
8 12 3 5 1 4 13 10 11 6 2 9 21
9 1 10 8 11 12 3 2 4 5 13 6 21
9 2 11 6 10 13 4 1 3 5 12 8 21
9 10 1 8 2 3 12 11 13 5 4 6 21
9 11 2 6 1 4 13 10 12 5 3 8 21
10 2 3 13 9 6 5 8 11 4 12 1 21
10 3 2 13 8 5 6 9 12 4 11 1 21
10 8 9 1 3 12 11 2 5 4 6 13 21
10 9 8 1 2 11 12 3 6 4 5 13 21
11 1 4 12 9 8 5 6 10 3 13 2 21
11 4 1 12 6 5 8 9 13 3 10 2 21
11 6 9 2 4 13 10 1 5 3 8 12 21
11 9 6 2 1 10 13 4 8 3 5 12 21
12 1 4 11 8 9 6 5 10 2 13 3 21
12 4 1 11 5 6 9 8 13 2 10 3 21
12 5 8 3 4 13 10 1 6 2 9 11 21
12 8 5 3 1 10 13 4 9 2 6 11 21
13 2 3 10 6 9 8 5 11 1 12 4 21
13 3 2 10 5 8 9 6 12 1 11 4 21
13 5 6 4 3 12 11 2 8 1 9 10 21
13 6 5 4 2 11 12 3 9 1 8 10 21
1 8 11 2 13 12 9 10 4 6 7 5 22
1 8 12 4 13 10 6 9 7 5 11 2 22
1 9 11 6 12 7 5 10 2 13 4 8 22
1 9 13 2 12 11 7 8 6 5 10 4 22
1 10 12 8 11 4 2 9 5 13 7 6 22
1 10 13 5 11 7 4 8 9 6 12 2 22
1 11 8 2 10 9 12 13 7 6 4 5 22
1 11 9 6 10 5 7 12 4 13 2 8 22
1 12 8 4 9 6 10 13 11 5 7 2 22
1 12 10 8 9 2 4 11 7 13 5 6 22
1 13 9 2 8 7 11 12 10 5 6 4 22
1 13 10 5 8 4 7 11 12 6 9 2 22
2 7 11 5 13 10 6 9 8 4 12 1 22
2 7 12 9 13 6 1 8 5 11 10 4 22
2 8 11 1 12 13 10 9 4 5 7 6 22
2 8 13 4 12 10 5 7 1 11 6 9 22
2 9 12 6 11 7 4 8 10 5 13 1 22
2 9 13 1 11 12 8 7 6 4 10 5 22
2 11 7 5 9 6 10 13 12 4 8 1 22
2 11 8 1 9 10 13 12 7 5 4 6 22
2 12 7 9 8 1 6 13 10 11 5 4 22
2 12 9 6 8 4 7 11 13 5 10 1 22
2 13 8 4 7 5 10 12 6 11 1 9 22
2 13 9 1 7 8 12 11 10 4 6 5 22
4 5 6 7 13 10 9 12 1 11 2 8 22
4 5 10 11 13 6 1 8 7 9 12 2 22
4 6 5 7 12 9 10 13 2 11 1 8 22
4 6 10 5 12 11 7 8 9 2 13 1 22
4 8 12 1 10 13 9 6 7 2 11 5 22
4 8 13 2 10 12 7 5 1 9 6 11 22
4 10 5 11 8 1 6 13 12 9 7 2 22
4 10 6 5 8 7 11 12 13 2 9 1 22
4 12 8 1 6 9 13 10 11 2 7 5 22
4 12 13 8 6 2 1 5 9 11 10 7 22
4 13 8 2 5 7 12 10 6 9 1 11 22
4 13 12 8 5 1 2 6 10 11 9 7 22
5 4 7 6 13 12 9 10 8 2 11 1 22
5 4 11 10 13 8 1 6 2 12 9 7 22
5 6 10 4 11 12 8 7 9 1 13 2 22
5 6 13 7 11 9 2 4 1 12 8 10 22
5 7 4 6 10 9 12 13 11 2 8 1 22
5 7 11 2 10 13 9 6 8 1 12 4 22
5 10 6 4 7 8 12 11 13 1 9 2 22
5 10 13 1 7 11 8 4 9 2 12 6 22
5 11 4 10 6 1 8 13 9 12 2 7 22
5 11 7 2 6 9 13 10 12 1 8 4 22
5 13 6 7 4 2 9 11 8 12 1 10 22
5 13 10 1 4 8 11 7 12 2 9 6 22
6 4 5 10 12 8 7 11 1 13 2 9 22
6 4 7 5 12 13 10 9 8 1 11 2 22
6 5 4 10 11 7 8 12 2 13 1 9 22
6 5 7 13 11 4 2 9 10 8 12 1 22
6 7 4 5 9 10 13 12 11 1 8 2 22
6 7 5 13 9 2 4 11 12 8 10 1 22
6 9 11 1 7 12 10 5 2 8 4 13 22
6 9 12 2 7 11 8 4 10 1 13 5 22
6 11 9 1 5 10 12 7 4 8 2 13 22
6 11 12 9 5 2 1 4 7 13 8 10 22
6 12 9 2 4 8 11 7 13 1 10 5 22
6 12 11 9 4 1 2 5 8 13 7 10 22
7 2 5 11 13 9 6 10 1 12 4 8 22
7 2 9 12 13 8 1 6 4 10 11 5 22
7 5 2 11 10 6 9 13 4 12 1 8 22
7 5 6 4 10 13 12 9 1 8 2 11 22
7 6 5 4 9 12 13 10 2 8 1 11 22
7 6 13 5 9 11 4 2 1 10 8 12 22
7 9 2 12 6 1 8 13 11 10 4 5 22
7 9 10 11 6 2 1 5 12 8 13 4 22
7 10 9 11 5 1 2 6 13 8 12 4 22
7 10 13 8 5 4 1 2 6 12 9 11 22
7 13 6 5 2 4 11 9 8 10 1 12 22
7 13 10 8 2 1 4 5 9 12 6 11 22
8 1 2 11 13 10 9 12 5 7 6 4 22
8 1 4 12 13 9 6 10 2 11 5 7 22
8 2 1 11 12 9 10 13 6 7 5 4 22
8 2 4 13 12 7 5 10 9 6 11 1 22
8 4 1 12 10 6 9 13 5 11 2 7 22
8 4 2 13 10 5 7 12 11 6 9 1 22
8 10 12 1 4 11 9 2 5 6 7 13 22
8 10 13 7 4 5 2 1 6 11 9 12 22
8 12 10 1 2 9 11 4 7 6 5 13 22
8 12 13 4 2 6 5 1 9 7 10 11 22
8 13 10 7 1 2 5 4 9 11 6 12 22
8 13 12 4 1 5 6 2 10 7 9 11 22
9 1 2 13 12 8 7 11 4 10 5 6 22
9 1 6 11 12 10 5 7 8 4 13 2 22
9 2 1 13 11 7 8 12 5 10 4 6 22
9 2 6 12 11 8 4 7 1 13 5 10 22
9 6 1 11 7 5 10 12 13 4 8 2 22
9 6 2 12 7 4 8 11 5 13 1 10 22
9 7 11 10 6 5 1 2 4 13 8 12 22
9 7 12 2 6 13 8 1 5 4 10 11 22
9 11 7 10 2 1 5 6 8 13 4 12 22
9 11 12 6 2 5 4 1 7 10 8 13 22
9 12 7 2 1 8 13 6 10 4 5 11 22
9 12 11 6 1 4 5 2 8 10 7 13 22
10 1 5 13 11 8 4 7 2 12 6 9 22
10 1 8 12 11 9 2 4 6 7 13 5 22
10 4 5 6 8 12 11 7 1 9 2 13 22
10 4 11 5 8 13 6 1 2 7 9 12 22
10 5 1 13 7 4 8 11 6 12 2 9 22
10 5 4 6 7 11 12 8 2 9 1 13 22
10 7 8 13 5 2 1 4 11 9 12 6 22
10 7 11 9 5 6 2 1 4 12 8 13 22
10 8 1 12 4 2 9 11 13 7 6 5 22
10 8 7 13 4 1 2 5 12 9 11 6 22
10 11 4 5 1 6 13 8 9 7 2 12 22
10 11 7 9 1 2 6 5 8 12 4 13 22
11 1 2 8 10 13 12 9 5 4 6 7 22
11 1 6 9 10 12 7 5 8 2 13 4 22
11 2 1 8 9 12 13 10 6 4 5 7 22
11 2 5 7 9 13 10 6 1 8 4 12 22
11 5 2 7 6 10 13 9 4 8 1 12 22
11 5 10 4 6 13 8 1 7 2 12 9 22
11 6 1 9 5 7 12 10 13 2 8 4 22
11 6 9 12 5 4 1 2 10 8 13 7 22
11 9 6 12 2 1 4 5 13 8 10 7 22
11 9 10 7 2 6 5 1 12 4 13 8 22
11 10 5 4 1 8 13 6 12 2 7 9 22
11 10 9 7 1 5 6 2 13 4 12 8 22
12 1 4 8 9 13 10 6 2 7 5 11 22
12 1 8 10 9 11 4 2 6 5 13 7 22
12 2 6 9 8 11 7 4 1 10 5 13 22
12 2 9 7 8 13 6 1 4 5 11 10 22
12 4 1 8 6 10 13 9 5 7 2 11 22
12 4 8 13 6 5 1 2 7 10 11 9 22
12 6 2 9 4 7 11 8 5 10 1 13 22
12 6 9 11 4 5 2 1 10 7 13 8 22
12 8 1 10 2 4 11 9 13 5 6 7 22
12 8 4 13 2 1 5 6 11 10 7 9 22
12 9 2 7 1 6 13 8 11 5 4 10 22
12 9 6 11 1 2 5 4 13 7 10 8 22
13 1 2 9 8 12 11 7 4 6 5 10 22
13 1 5 10 8 11 7 4 2 9 6 12 22
13 2 1 9 7 11 12 8 5 6 4 10 22
13 2 4 8 7 12 10 5 9 1 11 6 22
13 4 2 8 5 10 12 7 11 1 9 6 22
13 4 8 12 5 6 2 1 7 9 11 10 22
13 5 1 10 4 7 11 8 6 9 2 12 22
13 5 7 6 4 11 9 2 10 1 12 8 22
13 7 5 6 2 9 11 4 12 1 10 8 22
13 7 8 10 2 5 4 1 11 6 12 9 22
13 8 4 12 1 2 6 5 11 9 7 10 22
13 8 7 10 1 4 5 2 12 6 11 9 22
1,3 i 4 są fałszywe. 2 jest prawdziwe przy sumie trzech liczb narożnych równej 21, czyli bez 7.
Przykład rozmieszczenia liczb (rzędami):
(13), (3,2),(10),(5,8,9,6),(1),(12,11),(4).
Prawdziwe jest stwierdzenie – „dwie trójki przyrożne składają się wyłącznie z liczb nieparzystych”.
1
8 9
10
12 3 2 11
13
5 6
4
Dołożę jeszcze dwa interesujące stwierdzenia.
5. Suma liczb na przeciwległych ścianach sześcianu jest zawsze jednakowa.
6. Suma liczb na wszystkich ścianach jest taka sama.
Wszystkie 12 liczb, którymi oznaczamy krawędzie sześcianu, możemy podzielić na 4 rozłączne trójki przyrożne. Ponieważ suma każdej przyrożnej trójki jest taka sama, to suma wszystkich 12 liczb użytych do oznaczenia krawędzi musi się dzielić bez reszty przez 4.
Taki przypadek może zachodzić, gdy z 13 liczb usuniemy jedną z liczb: 3, 7 albo 11.
Usunięcie liczby 3 da nam sumę liczb przyrożnych równą 22. Dla liczby 7 ta suma jest równa 21 a dla 11 ? jest równa 20.
Przejdźmy teraz do prawidłowości wymienionych stwierdzeń.
1. Aby przyrożną trójką były 3 kolejne liczby dające sumę równą: 20, 21 albo 22, to tę trójkę może tworzyć jedynie liczba 6, 7 i 8. Ale dla tych liczb suma jest równa 21 a taką sumę uzyskamy tylko w przypadku wyrzucenia liczby 7. Daje to sprzeczność, czyli dla każdego rozwiązania stwierdzenie 1. jest fałszywe.
3. Ponieważ z trzynastu liczb możemy jedynie wyrzucić 3, 7 albo 11, to jak widać liczba 13 zawsze musi być użyta. Inaczej mówiąc, nie istnieje rozwiązanie, dla którego stwierdzenie 3. jest prawdziwe.
4. Przyrożna trójka złożona z potęg, mogła by być stworzona jedynie z liczb: 1, 4 i 9. Ale suma tych liczb to jedynie 14. Zatem stwierdzenie 4. jest zawsze fałszywe.
2. Analiza tego stwierdzenia jest bardziej złożona.
2.1. Istnieje rozwiązanie (z sumą 21), dla którego jest ono prawdziwe. Jedynym rozwiązaniem dla tego przypadku (nie licząc odbić i obrotów) to:
1
9, 8
10
11, 2, 3, 12
13
6, 5
4
2.2. Istnieje sześć – po trzy dla sumy 20 i 22 – istotnie różnych rozwiązań (tj. bez odbić i obrotów), dla których stwierdzenie 2 jest fałszywe. Jednym z nich jest np.:
4
13, 9
1
3, 6, 10, 7
2
12, 8
5
Pozdrawiam