Kwadratura żyrafy

30 listopada 2008
Marek Penszko

Przeglądając ostatnio domowe archiwum w poszukiwaniu rodowodu goszczących w poprzednim wpisie Klotsków, trafiłem na oryginalną przesuwankę – jedną z takich, jakie lubię. Może i Państwu się spodoba.

              

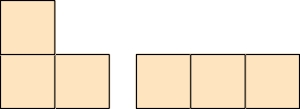
Z dziewięciu kwadratowych płytek ułożyłem żyrafę – tak mi podpowiada wyobraźnia; gdyby komuś nie podpowiadała, to zdjęcie przypomina, jak mniej więcej wygląda to coraz rzadsze zwierzątko.
Przesuwając po jednej płytce, żyrafę można zmienić w kwadrat w czterech ruchach na wiele sposobów.
Umówmy się jednak, że przesuwać wolno tylko po dwie płytki tak, jakby były one ze sobą połączone. Konkretne połączenie obowiązuje wyłącznie w danym ruchu. W następnym przesuwaną parę mogą tworzyć dowolne płytki, czyli jedną z nich może być także ta, która w poprzednim ruchu była w parze z inną. Przy takich zasadach z żyrafy uda się zrobić kwadrat w trzech ruchach, na przykład tak:
cd(ef) – gi(fh) – ab(dfi)
Przesuwana para (nie w nawiasie) powinna po przemieszczeniu dotknąć bokami płytek, których oznaczenia podane są w nawiasie; obrót w trakcie przesuwania wykonywany jest zawsze w lewo, oczywiście o kąt co najwyżej półpełny.
A teraz umawiamy się, że przesuwać należy po trzy płytki równocześnie, a więc zawsze tak, jakby tworzyły one jeden z dwóch kamieni triomina.

Czy uda się Państwu uporać z przesuwanką, czyli przekształcić żyrafę w kwadrat, w dwóch ruchach?