1111
11 listopada, czyli dwie jedenastki, albo cztery jedynki, albo liczba 1111… W pierwszej chwili para jedenastek może się kojarzyć numerologicznie i czasowo.
 11:11 to moja ulubiona godzina. Pamiętam słoneczne przedpołudnie, kiedy zobaczyłem ją na moim pierwszym, otrzymanym od ojca cyfrowym zegarku. Byłem wtedy w szkole i właśnie trwała duża przerwa. Od tamtej pory, ilekroć uda mi się uchwycić 11:11 na jakimkolwiek cyferblacie, wracam pamięcią do tamtego pierwszego razu i pierwszego zegarka. I liczę, ile lat już minęło.
11:11 to moja ulubiona godzina. Pamiętam słoneczne przedpołudnie, kiedy zobaczyłem ją na moim pierwszym, otrzymanym od ojca cyfrowym zegarku. Byłem wtedy w szkole i właśnie trwała duża przerwa. Od tamtej pory, ilekroć uda mi się uchwycić 11:11 na jakimkolwiek cyferblacie, wracam pamięcią do tamtego pierwszego razu i pierwszego zegarka. I liczę, ile lat już minęło.
Tak Grzegorz Turnau wyjaśniał tytuł wydanego przed trzema laty albumu „11:11”. Przy okazji wspomniał o tzw. „lightworkers”, czyli ludziach obarczonych jakoby misją kumulowania światła na naszej planecie, którzy przypisują liczbie 1111 właściwości magiczne. Zresztą nie tylko oni wierzą, że przypadkowe zauważenie tej liczby na wyświetlaczu, zwłaszcza zegarka cyfrowego, to jakiś omen.
Z arytmetycznych osobliwości liczby 1111 dwie są „okrągłe”: suma cyfr stu pierwszych liczb pierwszych równa się 1111, zaś tysiąc sto jedenastą liczbą w rosnącym ciągu złożonym z potęg (1, 4, 8, 9, 16, 25, 27, 32, 36, 49, …) jest milion. Wiadomo też, że 1111 jest liczbą 22-kątną oraz przypuszcza się, że jedynym kwadratem (jedyną potęgą?) z 1111 w środku jest 8111104 (2848^2).
Pora na łamigłówki. Zaczniemy od przystawki: jaką największą liczbę można zapisać czterema jedynkami?
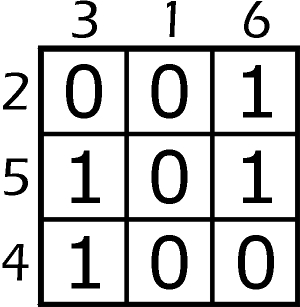
I kolej na dwa dania, oba z tej samej kuchni: krzyżówki zerojedynkowe. W każdej występują liczby złożone z zer i/lub jedynek, ale nie są to liczby zapisane w systemie dwójkowym. Niektóre z nich, krótsze niż n-cyfrowe, są dopełnione na początku zerami tak, aby wszystkie były tej samej długości, czyli składały się z n cyfr. Oto przykładowe rozwiązanie krzyżówki dla n=3.
Proszę zwrócić uwagę na dwie cechy, które będą istotne w zadaniach:
a) liczby wpisane są w rzędy (001, 101, 100) i kolumny (011, 000, 110) diagramu;
b) kolejność liczb, od najmniejszej do największej, oznaczona jest obok diagramu – przed rzędami i nad kolumnami (000, 001, 011, 100, 101, 110).
n=4
Do diagramu należy wpisać osiem liczb zerojedynkowych tak, aby liczby umieszczone obok diagramu oznaczały ich kolejność.
n=6
Do diagramu należy wpisać 11 podanych liczb oraz jedną nie podaną, o której wiadomo, że jej częścią jest liczba 1111. Jedenaście plus jedna cyfra znajdują się już na właściwych miejscach.



Komentarze
Przystawka: podejrzewam, że to liczbą jest 11 podniesione do 11 potęgi (chyba, że pozwolimy aby ostatnia jedynka stanęła na głowie i zaczęła krzyczeć – powstanie „wykrzyknik” i w konsekwencji 111! 😉 )
Danie pierwsze:
0110
0001
1100
0000
Danie drugie:
Brakująca liczba to 111110 (jej miejsce to ostatni wiersz).
Pozdrawiam 🙂
Zacznę od przystawki. Jeśli wolno użyć tylko samych czterech jedynek, to wydaje mi się , że największą będzie …
I tu mam kłopot, bo na tym forum może to być chyba tylko 1111 (przecież nie mogę użyć znaku „^”). Gdybym to miał zapisać w innym miejscu (np. kredą na tablicy), to napisałbym 11 do potęgi 11. Użycie innych znaków np. nawiasów i silni nie pozwala zapisać największej liczby. Bo jeśli komuś wydaje się, że taką znalazł, to wezmę ją w nawias i postawię na końcu „!”. 🙂
Przechodząc do dania dla jaroszy:
0 1 1 0
0 0 0 1
1 1 0 0
0 0 0 0
i dla mięsożernych:
1 1 0 0 1 1
0 0 0 1 1 0
1 0 1 0 0 0
0 0 0 0 1 0
1 1 0 1 1 0
1 1 1 1 1 0
I znów nie jestem z siebie zadowolony, bo choć zadania są dość nietypowe, to jednak niczego szczególnego nie wnoszą.
Pozdrawiam,
Jazz_off
Zdanie: „suma stu pierwszych liczb pierwszych równa się 1111” jest nieprawdą albo czegoś nie rozumiem.
Przystawka utknęła mi w gardle, a dopóki nie znajdę czegoś lepszego, to proponuję: (11!)^(11!), a jeśli silnia jest niewskazana, to 11^11.
Danie n=4:
0110
0001
1100
0000
Danie n=6:
110011
000110
101000
000010
110110
111110,
a brakująca liczba, to: 111110
Pozdrawiam
Najpierw zadanie – przystawka.
Bez podawnia działań, jakie można wykonywac – można napisac liczbę dowolnie dużą.
np.:
(((1111!)!)!)! …
czyli (1111 silnia) silnia….
A jeżeli założyc, że można wykonywac wyłącznie działania tj.: +, -, *, / oraz „zlepianie” jedynek, to 1111.
Jeżeli dołączyc potęgę, to 11 do potęgi 11.
Można też kombinowac z rónymi systemami niedziesiętnymi, silniami, itp.
Danie pierwsze:
0110
0001
1100
0000
I na koniec drugie danie:
110011
000110
101000
000010
110110
111110
W zdaniu: „przypuszcza się, że jedynym kwadratem (jedyną potęgą?) z 1111 w środku jest 8111104 (2848^2)”, czegoś brakuje, bo można podać nieskończenie wiele różnych liczb spełniających żądany warunek.
To zadanie wypada rozwiązać w ciągu 11 minut i najlepiej o godzinie 11:11 🙂
Zadanie n=4:
0110
0001
1100
0000
Zadanie n=6:
110011
000110
101000
000010
110110
111110
Takie zadania powinny „tygryski” lubić najbardziej, bo nic nie trzeba strzelać, a rozwiązanie układa się logicznie.
I diagram:
0110
0001
1100
0000
II diagram:
110011
000110
101000
000010
110110
111110
Lamigłówka:
11^11, a jeszcze więcej M^M
Andrzeju, tak to jest, gdy niezbyt dokładnie notuje się ciekawostki i przyjmuje je na wiarę. Niestety, nie pamiętam w tej chwili skąd wziąłem tę osobliwą osobliwość (nie jest pierwszej świeżości), ale nie ustaję w poszukiwaniach.
Za spostrzegawczość i dociekliwość dzięki oraz gratulacje okraszone rumieńcem.
mp
a co powiecie na takie coś: 1111^4 obliczcie to i powiedzcie jaki to ma związek z liczbami dwumianowymi:D