Czempiomaty
Aby uczestniczyć w eliminacjach do dwu Mistrzostw w Grach Matematycznych i Logicznych – najpierw VII Polski, a potem XXIII Międzynarodowych Francji – wystarczy dysponować czasem, ochotą oraz pewną kwotą (wpisowe od 20 do 50 zł). O zamiłowaniu do główkowania nie wspominam, bo to oczywiste. Nazwa imprezy brzmi elegancko, ale jest nieco zmyłkowa, więc na wszelki wypadek wyjaśniam, że nie chodzi o granie, tylko o rozwiązywanie zadań zaliczanych do tzw. matematyki rekreacyjnej. Do udziału zapraszają jak co roku od 17 lat: Wydział Podstawowych Problemów Techniki Politechniki Wrocławskiej oraz Oddział Wrocławski Polskiego Towarzystwa Matematycznego. Merytorycznie nad całością czuwa Francuska Federacja Gier Matematycznych. Podział na kategorie umożliwia start każdemu od lat 9 do 99.
Eliminacje są korespondencyjne i trwają do 15 grudnia; wiosną przyszłego roku odbędą się półfinały i finał krajowy, a latem najlepsi pojadą na międzynarodowy finał do Paryża. Szczegóły organizacyjne i zadania eliminacyjne znajdują się na stronie Wydziału PPT.
Kupić nie kupić, czyli startować nie startować, obejrzeć i porozwiązywać zadania można i warto. Wydaje się, że w tym roku Francuzi dla zachęty zaserwowali zestaw wstępny łatwiejszy niż w latach poprzednich. Na miękko rozwiązałem ostatnie zadanie (Kule armatnie w Monako), czyli z założenia najtrudniejsze – miałbym mały zgryz, gdyby tekst oderwać od rzeczywistości, pomijając w nim słowo „kilku”. Większość zadań ma charakter zabaw liczbowych, a niektóre są dość żmudne i w związku z tym, niestety, wiodą na pokuszenie, aby skorzystać z gotowych programów rozwiązujących dostępnych w Internecie. Inne, nawet te z środka stawki (np. Kleksy), zbliżają się niebezpiecznie stopniem trudności do konkursów audiotele. Najbardziej spodobała mi się Figura-zgadywanka – też prosta, ale oryginalna i trochę zabawna.
Łącząc kreskami punkty kratowe, należy narysować figurę C, która ma taki sam obwód, jak figura A i takie samo pole, jak figura B. Wystarczy podać jedno rozwiązanie.
„Punkty kratowe” brzmi groźnie, ale wiadomo o co chodzi. Napisałbym łagodniej – „węzły siatki”, zwłaszcza że nie ma mowy o układzie kartezjańskim. Zacytowałem to zadanie dla zachęty – rozwiązań proszę oczywiście nie nadsyłać w komentarzach. Natomiast mile widziane będą rozwiązania poniższego zadania, które pochodzi z finału pierwszego, jeszcze nie międzynarodowego Championnat 1987 De France des jeux mathematiques et logiques.
Magiczna piramida
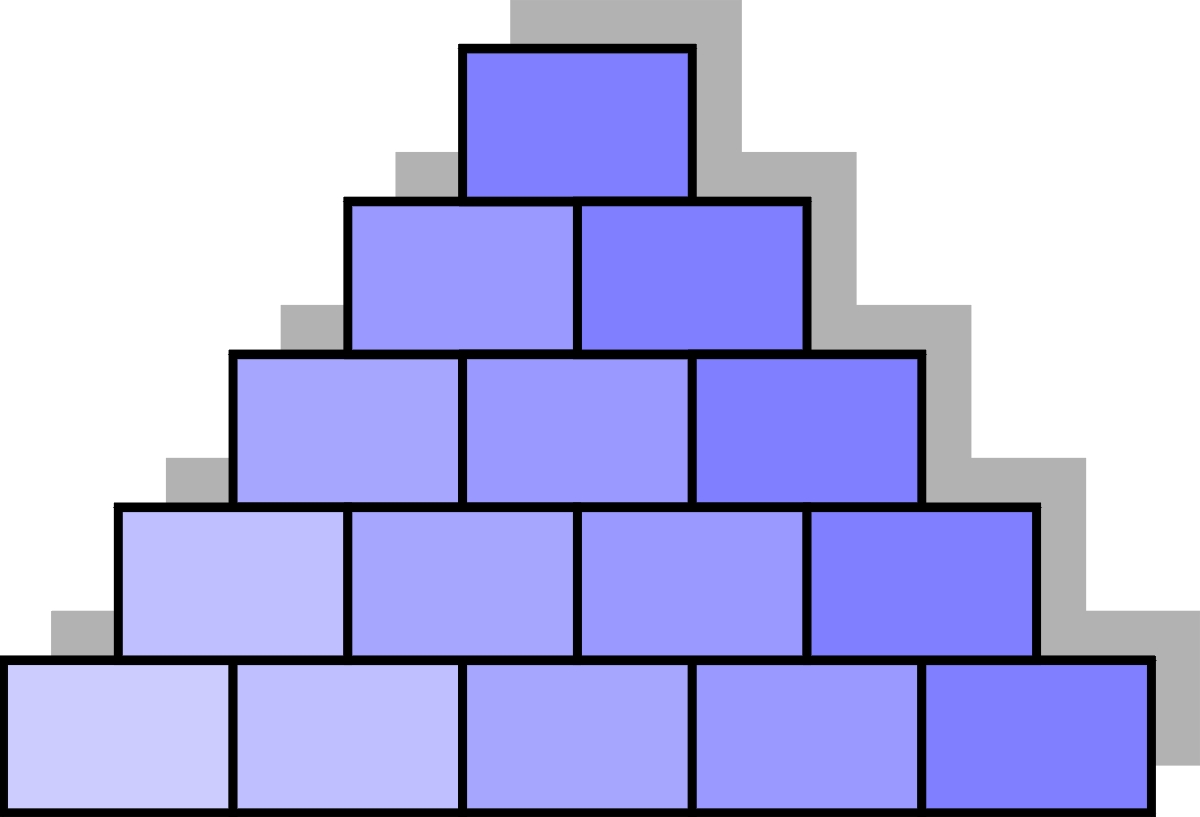
Do każdego pola należy wpisać inną liczbę całkowitą dodatnią taką, aby liczby w każdym rzędzie poziomym ustawione były w kolejności od najmniejszej do największej, ich suma była zawsze jednakowa, równa liczbie na szczycie, a ponadto – najmniejsza z możliwych. Minimalna powinna być także suma liczb w pięciu skrajnych najciemniejszych polach.
Ciekawostką jest fakt, że autorzy tego zadania przeoczyli pewien drobiazg, który ujawniony został dopiero na finale przez rozwiązujących. O jaki drobiazg chodzi – to dodatkowa zagadka.

Komentarze
Nie powiedziano czy od najmniejszej do największej
to z lewa na prawo czy odwrotnie.
Jeśli o to chodziło. ale nie powiedziałbym, że to przeoczenie – mogło to być świadome działanie, bo w obu przypadkach: Minimalna suma liczb w pięciu skrajnych najciemniejszych polach jest inna i np. autorom chodziło o tą faktycznie najmniejszą.
empiotrze, przeoczenie dotyczące kolejności jest moje (jeśli to przeoczenie). Chodzi o kolejność jak w wojsku (kolejno odlicz!), i w alfabecie, i w ciągu liczbowym, i w ogóle, czyli od lewej do prawej. Przeoczenie autorów jest natomiast czymś w rodzaju drobnej „niedoróbki”, która i w Łamiblogu już nieraz się zdarzała.
mp
To pewnie chodzi o okreslenie:
… ich suma była zawsze jednakowa, równa liczbie na szczycie …
Nie jest tu powiedziane konkretnie, że ma to być taka sama suma w każdym rzędzie, a nie suma 14 liczb pod tą najwyżej położoną…
empiotrze, zimno. Mam wrażenie, że słówko „zawsze” wyjaśnia sprawę, czyli jest pięć równych minimalnych sum – oczywiście w przypadku górnej liczby „suma” jest równa tej liczbie.
mp
Pewnie to, ze najmniejsza możliwa suma pięciu najciemniejszych pól nie jest realizowana dla najmniejszej sumy w wierszu. Ale wg mnie to jest prawidłowe bo dla najmniejszej sumy „wierszowej” są możliwe różne sumy „ciemnych” pól więc chcą tą najmniejszą. 🙂
Także nie o to chodzi.
Może podpowiedzią będzie informacja, że przeoczony drobiazg nie tyle został przez rozwiązujących ujawniony, co ujawnił się sam.
mp
Poddaję się … 🙂
27
13,14
1,11,15
2,6,9,10
3,4,5,7,8
a suma to 74.
Kiedy zobaczyłem rysunek piramidy, to wmówiłem sobie, że mam do czynienia z trójkątem Pascala i … nie mogłem zrozumieć treści zadania. Natomiast po chwilowym wymazaniu z pamięci owego trójkąta treść zadanie wydała się jasna.
Magiczna piramida ma co najmniej 3 rozwiązania i to być może jest tym zagadkowym drobiazgiem tak często nie lubianym przez układających zadania.
Pozdrawiam
Andrzeju, tak, właśnie o ten drobiazg chodzi, ale żeby aż co najmniej trzy? Francuzi przyznali się do deux solutions possibles…
mp
Jeżeli Francuzi przyznają się do deux solutions possibles … , to ja nie przyznaję się do znalezionych przeze mnie trzech rozwiązań. Okazało się, że jeden z „króliczków” był fałszywy (kłopoty z dodawaniem).
27
13-14
1-11-15
2-6-9-10
3-4-5-7-8
27
13-14
1-11-15
3-5-9-10
2-4-6-7-8
Pozdrawiam
Mam dwa rozwiązania:
27
13, 14
1, 11, 15
2, 6, 9, 10
3, 4, 5, 7, 8
oraz
27
13, 14
1, 11, 15
3, 5, 9, 10
2, 4, 6, 7, 8
Jak ma się plan, to rozwiązanie idzie jak po sznurku, jednak nad tym planem trochę się namęczyłem.
A oto zarys metody rozwiązania:
1. Musimy ustalić jaką najmniejszą liczbę n należy wstawić w miejsce 15 aby
1+2+…+14+n <=5n.
Tą liczbą jest 27 i ona będzie na szczycie piramidy.
2. Następnie należy ustalić jakie kombinacje czternastu liczb naturalnych dadzą w sumie 4*27 czyli 108. Są 3 takie kombinacje:
1, 2, … , 10, 11, 12, 13, 17
1, 2, … , 10, 11, 12, 14, 16
1, 2, … , 10, 11, 13, 14, 15
3. Na drugi (od góry) rządek z każdej kombinacji wybieramy dwie liczby dające w sumie 27. Może to być 10 i 17, 11 i 16, 13 i 14. Ostatnia kombinacja jest najlepsza, bo liczba większa z pary jest najmniejsza.
4. Do wypełnienia trzech dolnych rzędów piramidy pozostają:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 15
Na środkowy rządek wybieramy te z nich, które dają w sumie 27 i grupują dwie największe. Będzie to 1, 11 i 15.
5. Na dwa dolne rządki piramidy pozostają:
2, 3, 4, 5, 6, 7, 8, 9, 10
Na drugi od dołu rządek wybieramy 4 liczby, dające w sumie 27 i grupujące dwie największe. Może to być:
2, 6, 9, 10
lub
3, 5, 9, 10.
Daje to dwa – przedstawione powyżej – rozwiązania.
Z pozdrowieniami,
Jazz_off
PS
Nie poznaliśmy (przynajmniej ja nie poznałem) rozwiązania usztywnienia rozchwianego szkieletu sześcianu w wersji z linami. Czy mógłby Pan, Panie Marku, napisać coś na ten temat?
Jazz_onie, pozostawię sprawę otwartą jeszcze przez 2-3 tygodnie. Może przez ten czas ktoś zaproponuje jakieś rozwiązanie. Jakkolwiek by nie było, po tym czasie powrócę do tematu „usztywniania” sześcianu i innych brył.
mp