Koniec Wieczności
Trzy i pół roku temu w sprzedaży pojawiła się układanka Eternity II, wydana przez angielską firmę zabawkarską Tomy. 50 dolarów (u nas 150 złotych), zainwestowanych w jej zakup, było równocześnie jakby wpisowym w konkursie z nagrodą opiewającą na 2 miliony dolarów. Aby zainkasować tę kwotę wystarczyło odpowiednio poskładać wszystkie elementy i przesłać rozwiązanie pod wskazany adres, no i oczywiście być pierwszym nadawcą takiej przesyłki.
Pomysłodawcą całego zamieszania był angielski dziennikarz Christopher Monckton, znany wcześniej z podobnej łamigłówki o nazwie Eternity, za uporanie się z którą wypłacono nagrodę w wysokości miliona funtów.
Konkurs z „drugą wiecznością” trwał do końca 2008 roku, ale ponieważ rozwiązanie nie wpłynęło, został przedłużony o dwa lata. Niedawno na stronie firmowej pojawiła się informacja o definitywnym zakończeniu zabawy oraz zapowiedź następnych podobnych.
Z układanką nikt się nie uporał. Żadnego rozwiązania autorskiego nie podano – podobno są ich tysiące, choć nie byłbym zaskoczony, gdyby nie było… ani jednego i okazałoby się, że organizatorzy nabili klientów w butelkę.
O Eternity II pisałem, gdy debiutowało. Przypomnę: chodziło o ułożenie dużego kwadratu (16 x 16) z 256 małych. Każdy mały kwadrat podzielony był przekątnymi na cztery trójkąty prostokątne, a na każdym trójkącie znajdował się jeden z 17 symboli. Kwadraty w rozwiązaniu powinny się stykać jednakowymi symbolami.
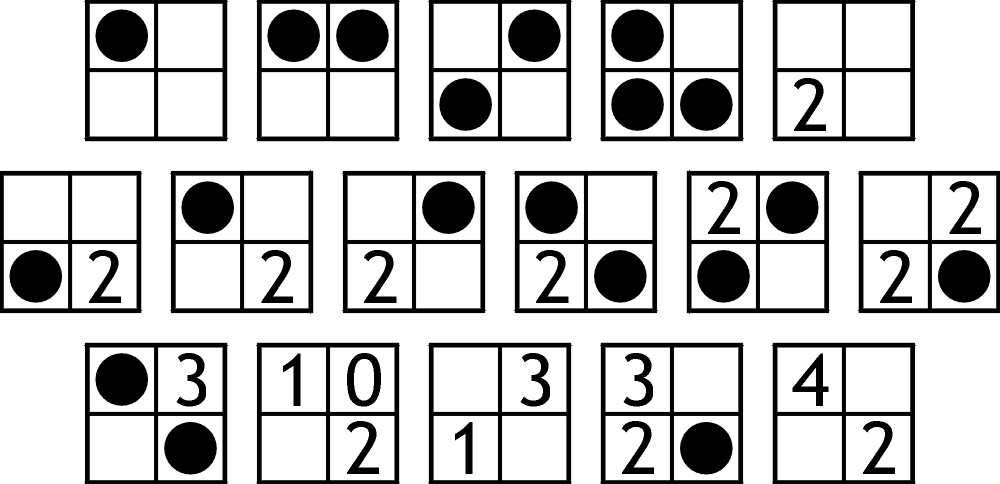
Dawniej na stronie firmowej była wprawka z 16 wybranych kwadratów. Wyglądała tak:
Z lewej strony surowce – kwadraty ułożone na chybił-trafił, z prawej – jak należy, czyli rozwiązanie układanki 4 x 4.
Przed trzema laty do boju ruszyła armia informatyków zbrojna w komputery, ale była to walka z wiatrakami, bo najszybsze maszyny, nawet kooperujące w dużej grupie w ramach tzw. platformy BOINC, są bezradne wobec ogromu kombinacji, jakie należałoby sprawdzić (liczba grubo ponad 600-cyfrowa). Chodziło więc raczej o to, by pomóc szczęściu, a praktycznie łamigłówka, choć niby z pełną informacją, była bliska loterii. Pojawiło się wprawdzie kilka publikacji naukowych na temat sposobu zmagania się z kwadratami, ale dotyczyły one metod heurystycznych, czyli na skróty i z grubsza, a więc bez pewności dotarcia do 2 milionów.
Układanka Eternity II, jeśli chodzi o podstawową zasadę, jest bardzo podobna do klasycznej łamigłówki Tetravex z rozrywkowego pakietu Windows sprzed 22 lat, dziś dostępnej za friko (ja grywam tu). Tetravex jest jednak bardziej przyjazny, bo mniejszy i kwadratów się w nim nie obraca.
Mam nadzieję, że przyjazna okaże się również poniższa łamigłówka, należąca do tej samej rodziny, zwanej z angielska edge-matching (pasowanki brzegowe).
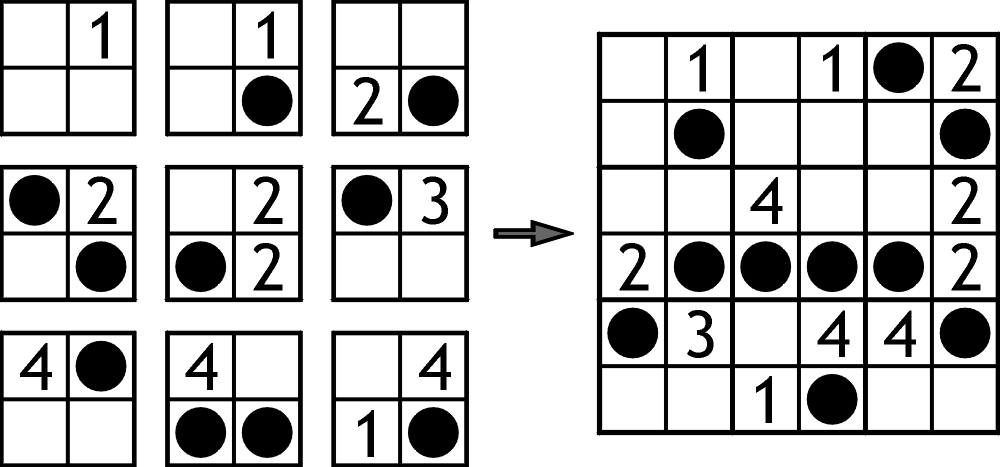
Diagram 8 x 8 z rozwiązaniem łamigłówki zwanej saperem lub polem minowym rozcięto na 16 kwadratów 2 x 2:
Proszę odtworzyć, czyli poskładać diagram. W rozwiązaniu wystarczy podać, ile min jest na obu przekątnych.
Gwoli jasności poniżej mniejsza łamigłówka (9 kwadratów) z rozwiązaniem. Jak widać elementów, jak w Tetraveksie, nie należy obracać.
Z przykładu łatwo wywnioskować podstawową zasadę sapera (jeśli ktoś jej nie zna): cyfra w danej kratce oznacza, w ilu polach stykających się z tą kratką – bokiem lub rogiem – są miny.
PS Ściśle rzecz biorąc, układ min na ułożonym diagramie 8 x 8 nie będzie jedynym rozwiązaniem zadania, które powstałoby po usunięciu min; jest tylko jednym z układów spełniających warunki sapera.
Nie muszę chyba dodawać, że kwadratów nie trzeba wycinać – wystarczy, zerkając na nie, tworzyć rysunek zaminowanego diagramu na kartce w kratkę. Chyba nie będzie to trudne, ale może się mylę.



Komentarze
Czy łamigłówka, pasowanki (niepasowanki) brzegowe, to nie jest nabijanie w butelkę?
Skąd takie podejrzenie?
mp
\ – 4
/ – 2
Według mnie zadanie trudne. Sporo czasu nad nim spędziłem. Ale satysfakcja olbrzymia.
Na przekatnych jest 6 min
xxoxox10
o22ooox2
x23x4xoo
2o2ox2xx
oxxxo3xo
x22xxoox
2oxox3ox
ox2x1xxx
Trudne, wiec niezbyt przyjazne, ale przyjemnie jest dotrzec do celu.
a
Panie Marku!
Dziś mamy 11.02.2011 co bez separatorów daje ładną bo symetryczną liczbę 11022011. Na wzór niemiecki, pić z tej okazji nie zamierzam, ale może warto coś z tym zrobić? Następna taka okazji będzie za rok. Kolejna, no właśnie, kiedy będzie kolejna? Dlatego zachęcam wykorzystać taką okazję do zadania stosownego zadania 😉
Pozdrawiam serdecznie,
zj
Jazzie, właściwie to zadanie zostało zadane, więc nic tu po mnie 😉
Z drugiej strony zabawnie się składa, bo przypadkiem mam na tapecie pewien mały test zero-jedynkowo-dwójkowy (ale nie palindromowy). Powstał nie do Łamiblogu, ale nie będzie grzechem tu go zaprezentować, co zapewne uczynię przy okazji ostatniej w tym roku zimowej (bo będą jeszcze jesienne) daty typu 0-1-2, czyli 22.02.2011.
Zdravi moc
mp
Myślałem, że łamigłówka z diagramu 8×8, to mały żarcik i zadanie nie ma rozwiązania.
Podczas rozwiązywania nie mogłem poradzić sobie z wolnymi minami, tj. takimi, których nie można przyporządkować do żadnej liczby. Byłem przekonany, że w łamigłówce zachodzi następująca relacja stykania się:
jeżeli liczba, to mina
oraz
jeżeli mina, to liczba,
tak jak to widać w przykładzie z dziewięcioma kwadratami.
Prawdopodobnie nie rozumiem na czym polega gra – saper.
PS Przykładowa łamigłówka z dziewięcioma kwadratami może mieć inne rozwiązanie (inaczej można rozmieścić kwadraciki 2×2).
Z „niewyliczonymi” minami rzeczywiście był kłopot. W normalnym saperze mogą się takie trafiać, jeśli na początku jest podane, ile powinno być wszystkich min (brakującymi do pełnego zestawu wypełnia się wówczas pola nie sąsiadujące z liczbami). Ten saper-układanka nie był jednak całkiem normalny, bo (o czym uprzedzałem) był jednym z wielu rozwiązań zadania, czyli jako klasyczny saper trafiłby do kosza.
mp
Jazzie, 11.02.2011 był ostatnim palindromicznym dniem.
Kolejnych już nie będzie!
Dlaczego?
Jak przypomnisz sobie jeden ze starszych wpisów na „Łamiblogu”, to będziesz wiedział(a).