Dostatecznie duża
Część znajdującego się pod poprzednim wpisem komentarza Andrzeja dotyczy tematu, który postanowiłem rozwinąć. Andrzej nawiązał do artykułu zamieszczonego w numerze styczniowym „Świata nauki”, którego fragment brzmi tak:
„W 1923 roku dwaj brytyjscy matematycy Godfrey Hardy i John Littlewood wysunęli hipotezę bezpośrednio wiążącą liczby pierwsze z kwadratami: każda dostatecznie duża liczba naturalna jest albo kwadratem, albo sumą kwadratu i liczby pierwszej. Komputerowe łowy na liczbę, która by obalała tę hipotezę, nie powiodły się, ale jej dowodu jak dotąd nie znaleziono”.
Andrzej zadał dwa pytania. Zacznę od drugiego, aby potem niepostrzeżenie przejść do pierwszego: co to jest dostatecznie duża liczba? Takie pytanie już kiedyś w Łamiblogu zadawałem, licząc na Państwa wyjaśnienie, ale nikt się nie ośmielił, więc korzystając z okazji spróbuję sam.
Pojęcie dostatecznie duża należy do matematyki „mglistej” oraz „humorystycznej”. Pojawia się zwykle w teorii liczb jako warunek prawdziwości jakiegoś twierdzenia i oznacza pewną liczbę, powyżej której to twierdzenie jest prawdziwe. Mówiąc ściślej, dostatecznie duża liczba x znaczy to samo, co większa od jakiejś liczby a, której wartości nie znamy. Gdybyśmy ją znali, to zamiast dostatecznie duża w twierdzeniu byłoby podane konkretnie: każda liczba naturalna większa od – powiedzmy – 44… itd.
A dlaczego to sformułowanie jest humorystyczne? Ponieważ stanowi żartobliwe uzasadnienie, że równość 2 + 2 = 5 jest prawdziwa dla… dostatecznie dużych dwójek.
Nietrudno, sprawdzając kolejne liczby, trafić na takie, które hipotezy Hardy’ego-Littlewooda nie spełniają. Najmniejszą jest 10, a kolejne to 34, 58, 85, 91, 130 itd., aż do 21679 i… koniec? Jak dotąd wszystko wskazuje na to, że tak, więc zapewne w hipotezie H-L zamiast dostatecznie duża można by wstawić większa od 21679, ale pewności nie ma, bo dowodu brak.
Pozostając przy kwadratach i liczbach pierwszych, proponuję zmierzyć się z krzyżówką liczbową.
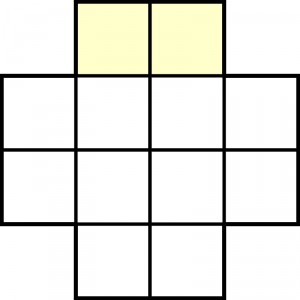
Do diagramu należy wpisać 12 cyfr, które powinny utworzyć w rzędach i kolumnach osiem różnych liczb – cztery 4-cyfrowe i cztery 2-cyfrowe. Siedem z nich powinno być kwadratami, jedna – żółta – nie. W zasadzie nie muszę dodawać, że ta jedynaczka będzie liczbą pierwszą, bo rozwiązanie i bez tej informacji byłoby jedno. A czy to dopowiedzenie ułatwia rozwiązywanie? Zapewne tak, ale jeszcze łatwiej będzie tym z Państwa, którzy uważali na Łamiblogowych lekcjach i pamiętają tę.

Komentarze
Czy 13 i 31 spełniają hipotezę Hardy’ego-Littlewooda?
Mnie udało sie znaleźć przykłady dla tych liczb tylko przy założeniu, że dopuszczalne są kwadraty liczb urojonych. Wtedy mamy np. 13=17-4 i 31=47-16
Tak. Każda liczba pierwsza p = 0^2 + p.
mp
Rozwiązanie:
_71_
2304
5929
_64_
Jest jeszcze pięć innych z felerem, np.
_11_
8100
1521
_64_
Feler to liczba zapisana z zerem wiodącym.
Liczby poziomo: 71, 2304, 5929, 64
Pionowo: 25, 7396, 1024, 49.
Rzedami od gory:
71, 2304, 5929, 64
a
Określenie: liczba „dostatecznie duża”, nie wzbudziło we mnie śmiechu i traktuję je jako zwykły skrót myślowy a w hipotezie Hardy’ego-Littlewooda rozumiem je tak, że liczb niespełniających tej hipotezy jest skończenie wiele.
Natomiast mam wątpliwości do fragmentu tekstu zamieszczonego w „Świecie nauki” sugerującego, że znalezienie kolejnej liczby niespełniającej hipotezy Hardy’ego-Littlewooda obalałoby tę hipotezę. Chyba jedynie mówiłoby, że tą „dostatecznie dużą” liczbą nie jest 21679?
Pozdrawiam,
Jazz
Święta racja. „Obalenie” zostało obalone.
mp