Tylko siedem
Nob Yoshigahara, znany japoński spec od łamigłówek, miał słabość do dwóch ich rodzajów – manipulacyjnych i liczbowych. Łamigłówki manipulacyjne to po prostu zabawki dla rąk i głowy – w rodzaju różnych układanek lub kostki Rubika, która właściwie też jest układanką i której właśnie stuknęło pół wieku.
Od łamigłówek liczbowych roi się w książkach Noba, których większość (ponad 50) wydano tylko w Japonii; po angielsku ukazały się zaledwie dwie. W obu jest następujący liczbowy orzeszek:
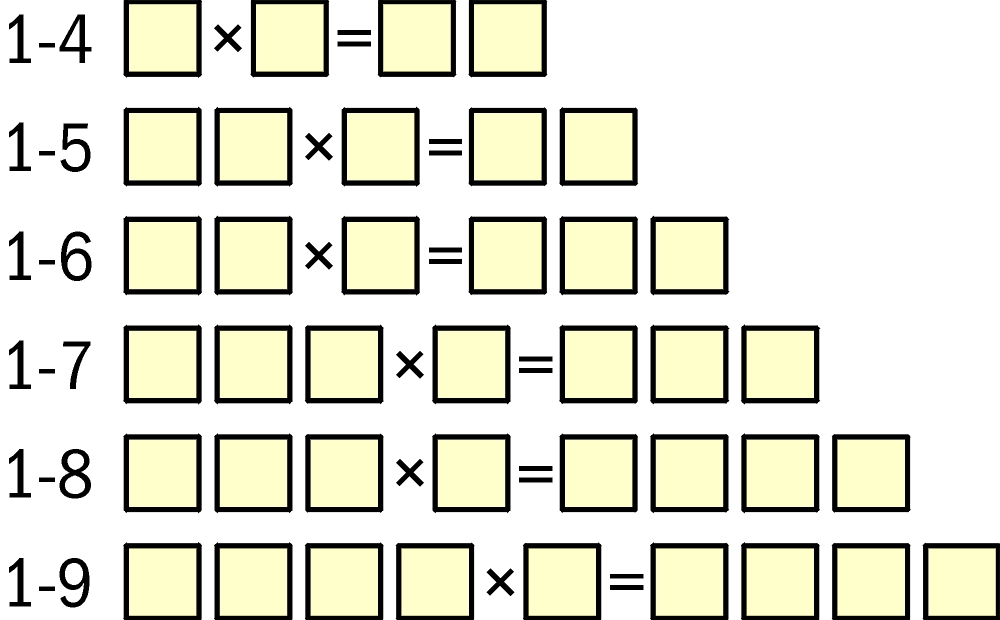
Do kratek w każdym rzędzie należy wpisać różne cyfry z zakresu podanego z lewej strony – tak, aby każde mnożenie było poprawne. Gwoli jasności, rozwiązaniem najprostszego pierwszego działania jest 3×4=12 (lub 4×3=12).
Rozszyfrowanie mnożenia dla zakresu 1-5 także nie jest trudne, bo pomocna jest ogólna zasada, wykluczająca z określonych kratek 1 i 5, co pozwala od razu ulokować te cyfry w konkretnych polach. Jednak dla kolejnych działań zaczynają się schody – moim zdaniem dla trzech ostatnich zakresów zbyt żmudne, praktycznie nie do pokonania „na piechotę”. Co gorsza dla zakresów 1-8 i 1-9 są po dwa rozwiązania, a dla 1-7 rozwiązań brak.
Proponuję modyfikację zabawy liczbowej dla zakresu 1-7, aby uzyskać rozwiązanie. Proszę spróbować utworzyć równość zawierającą tylko siedem różnych cyfr od 1 do 7, operując wyłącznie czterema podstawowymi działaniami bez nawiasów. Eleganckim przykładem dla zakresu 1-5 byłaby równość 12-3-4=5, a mniej eleganckim 1×5-4:2=3.
Ponadto, co widać w przykładach, działania mogą występować tylko po lewej stronie równości; po prawej powinien być jedynie wynik.
Zapewne obecność rozwiązania będzie okupiona obfitością rozwiązań.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
_ _ x _ + _= _ _ _
2 3 x 7+ 4 = 1 6 5
4) 3*4=12
5) 13*4=52
6) 54*3=162
7) Trzy przykładowe
54*7/3=126
45*7+6=321
43*6-1=257
8)
582*3=1746
453*6=2718
9)
1963*4=7852
1738*4=6952
24×7-3=165
Rozwiązania:
1-5: 13 x 4 = 52
1-6: 54 x 3 = 162
1-7: brak
1-8: 453 x 6 = 2718 lub 582 x 3 = 1746
1-9: 1738 x 4 = 6952 lub 1963 x 4 = 7852
Dla 1-7 można by rozważyć na przykład takie równanie:
_ _ _ / _ _ + _ = _
które ma jedynie 2 rozwiązania (216/54 + 3 = 7 lub 235/47 + 1 = 6).
Na razie to przykład z najmniejszą liczbą rozwiązań jaki znalazłem, ale jeszcze poszukam 🙂
Kolejne cyfry:
7*6-5-4-32=1
7+6*5-4-32=1
Ułamki:
3/2+6/4+5-7=1
Wszystkie cztery działania:
3*6/2+4-5-7=1
i tak dalej…
Panie Marku, wykorzystam to miejsce, aby zwrócić uwagę na jedną rzecz w grudniowym Świecie Nauki. Na stronie 73 napisał Pan, że liczba meczów, przewodów łączących elementy sieci i uścisków dłoni w grupie wynosi LT=Tn, czyli n(n+1)/2 Jednak ta liczba wynosi T(n-1), czyli n(n-1)/2.
Ten wzór jest często potrzebny np. przy liczeniu wariancji sumy zmiennych losowych o takim samym rozkładzie, które nie są niezależne (gdy są niezależne, to wtedy po prostu wariancja sumy to suma wariancji). Wtedy wzór ten wygląda mniej więcej tak:
Var(X1+…+Xn)=Var(X1) + … + Var(Xn) + 2*Cov(Xi,Xj) dla i j.
Zawsze wyzwaniem dla głowy jest wyobrażenie sobie liczby elementów kowariancji, które trzeba zsumować. Tu pomocne są liczby trójkątne, bo liczba tych elementów to właśnie liczba uścisków dłoni.
Wyobrażam sobie to tak: mamy kwadrat n × n, z którego usuwamy przekątną (nikt sam się ze sobą nie wita; a w odniesieniu do wzoru na wariancję – ta przekątna to są wariancje każdej zmiennej z osobna, bo Cov(X,X)= Var(X)). Mamy więc n × n – n, czyli n(n-1). Następnie zostają mi dwa trójkąty, z których muszę usunąć jeden, bo nie chcę 2 razy liczyć każdego uścisku dłoni. W odniesieniu do wzoru na wariancję, mamy tam na stałe 2*Cov(i,j), bo Cov(i,j)=Cov(j,i), nie chcemy więc uwzględniać tego podwójnie. Ostatecznie uzyskujemy n(n-1)/2, czyli T(n-1).
https://oeis.org/A000217 – n(n+1)/2. Oba wzory dają liczby trójkątne, ale oczywiście racja, że w przypadku meczów n drużyn, uścisków dłoni n osób itp. właściwym jest wzór z minusem.
mp
13 × 4 = 52
54 × 3 = 162
— (na rozwiązanie dla 1- 7 przyjdzie czas) —
453 × 6 = 2718
582 × 3 = 1746
1738 × 4 = 6952
1963 × 4 = 7852
582 * 3 = 1746
453 * 6 = 2718
Uzupełnienie – wybrane rozwiązania dla 1-7 (jest ich multum, więc subiektywnie wybrałem kilka moim zdaniem eleganckich):
1+2-3-4+5+6 = 7
1-2+3+4-5+6 = 7
1-2*3*4+5*6 = 7
1/2*3*4-5+6 = 7
1+2*35-4 = 67
12/3+4+5-6 = 7
1+2+34-5*6 = 7
1963 * 4 = 7852
1738 * 4 = 6952