Stopniowanie swobód

30 listopada 2024
Marek Penszko

Przygotowuję zadania do przyszłorocznego „Omnibusa”, a w trakcie tej czynności pojawiają się odpady. Określenie to dotyczy wyłącznie skutków procesu, a nie jakości, czyli niektóre zadania odpadają z jakichś mało istotnych, ale nie merytorycznych względów; zwykle po prostu dlatego, że jest ich za dużo, więc trzeba jakieś odrzucić – prawie losowo. Zaś odpady są jak surowce wtórne – mogą pojawić się w innym miejscu, np. w Łamiblogu.
Poniższe odpadowe zadanie należy do rodzaju, który już tu kiedyś gościł, ale to było ponad dekadę temu, więc warto je przypomnieć – zwłaszcza że jest (moim zdaniem) ciekawe, oryginalne i nieproste.
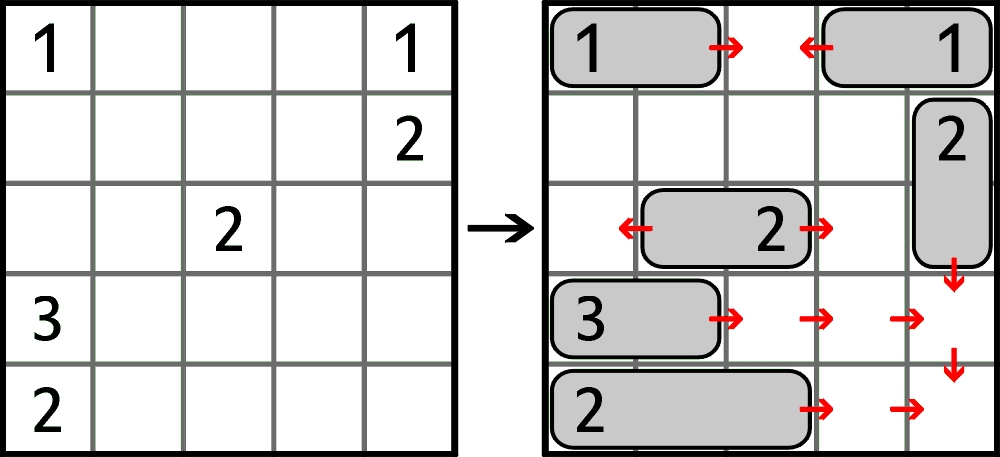
Diagram jest parkingiem, na którym stoją auta – prostokąty 1×2 (każdy zajmuje dwa pola) i 1×3 (każdy na trzech polach). Na każdym aucie jest jedna cyfra, która oznacza liczbę jego „stopni swobody”, czyli liczbę wolnych pól, na które można przemieszczać to auto do przodu i do tyłu.
Auta usunięto z diagramu – pozostały tylko cyfry. Należy odtworzyć rozmieszczenie aut, pamiętając o dodatkowym warunku: kratki nie zajęte przez auta powinny tworzyć spójny obszar (jeden wielokąt). Czerwone strzałki na rozwiązaniu przykładu wskazują na stopnie swobody aut.
W rozwiązaniu wystarczy podać liczby aut małych i dużych stojących na parkingu (w przykładzie M-5, D-1).
PS stopnie swobody aut nie mają oczywiście nic (lub prawie nic) wspólnego z pojęciem stopni swobody w fizyce, ani tym bardziej w statystyce.
Przykład

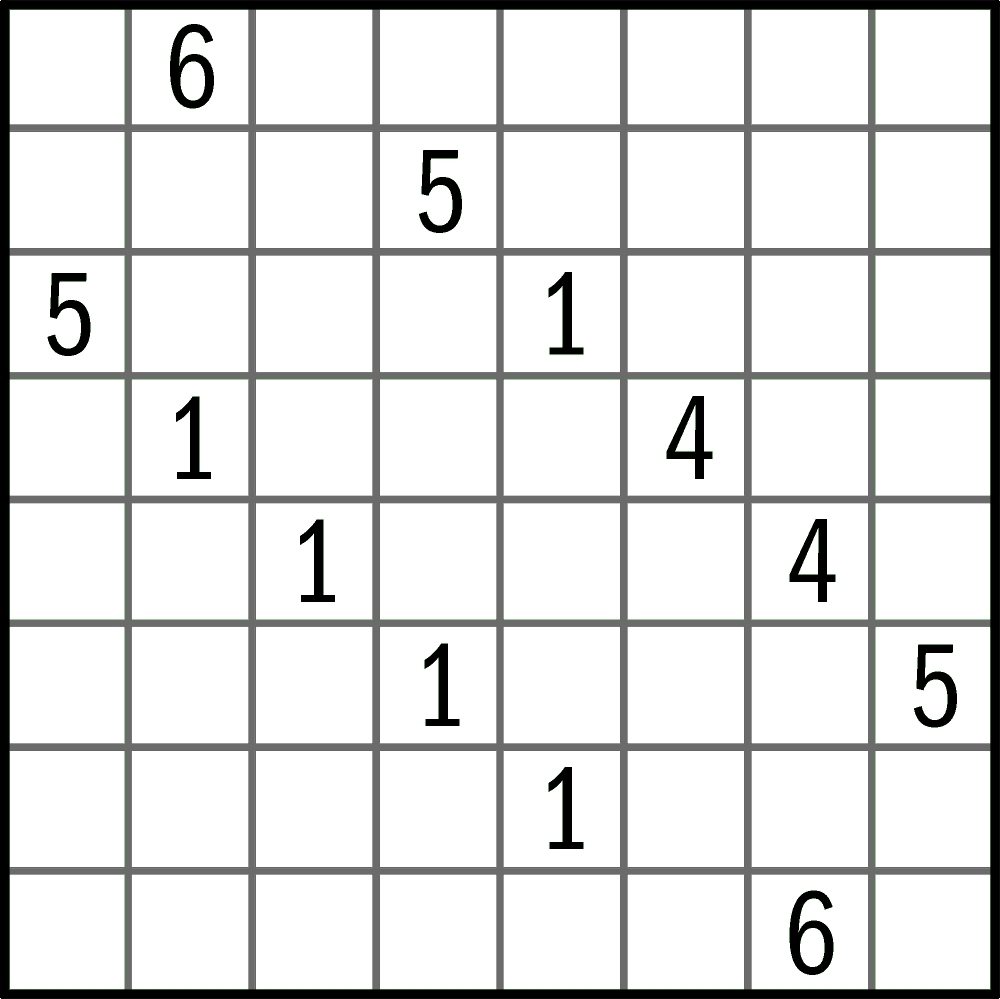
Zadanie

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.