Dwa szkielety

14 września 2024
Marek Penszko

Mnożenie jest najpopularniejszym działaniem w arytmetyce szkieletowej. Przypomnę, że chodzi o dziedzinę matematyki rekreacyjnej, obejmującą zadania, które polegają na rekonstruowaniu działań na podstawie ich „szczątków”. Szczątkami jest właśnie „szkielet”, czyli ujawnione wszystkie miejsca po cyfrach, tworzących słupkowe działanie oraz z reguły kilka cyfr, zajmujących niektóre z tych miejsc. Mnożenie ma priorytet przed innymi działaniami ze względu na podpowiedzi, którymi są iloczyny cząstkowe. Wprawdzie w dzieleniu w słupku także pojawiają się iloczyny cząstkowe, ale zapis mnożenia jest bardziej zwarty, więc łatwiej zauważyć i wykorzystać logiczne zależności między cyframi oraz zwykle w niewielkim stopniu korzystać z metody prób i błędów.
Ojczyzną szkieletowych mnożeń jest Kraina Kwitnącej Wiśni, którą można by także nazwać Krainą Łamigłówek – zwłaszcza po nie tak dawnej pandemii sudoku, bo jej ogniskiem była właśnie Japonia. Są one tam znane od XVIII w. jako molowe rachunki, czyli działania, których zapis powygryzały mole. Przybierają niekiedy ekstremalną, karykaturalną formę, która służy raczej do łapania się za głowę, niż do jej łamania – jak na poniższym obrazku.

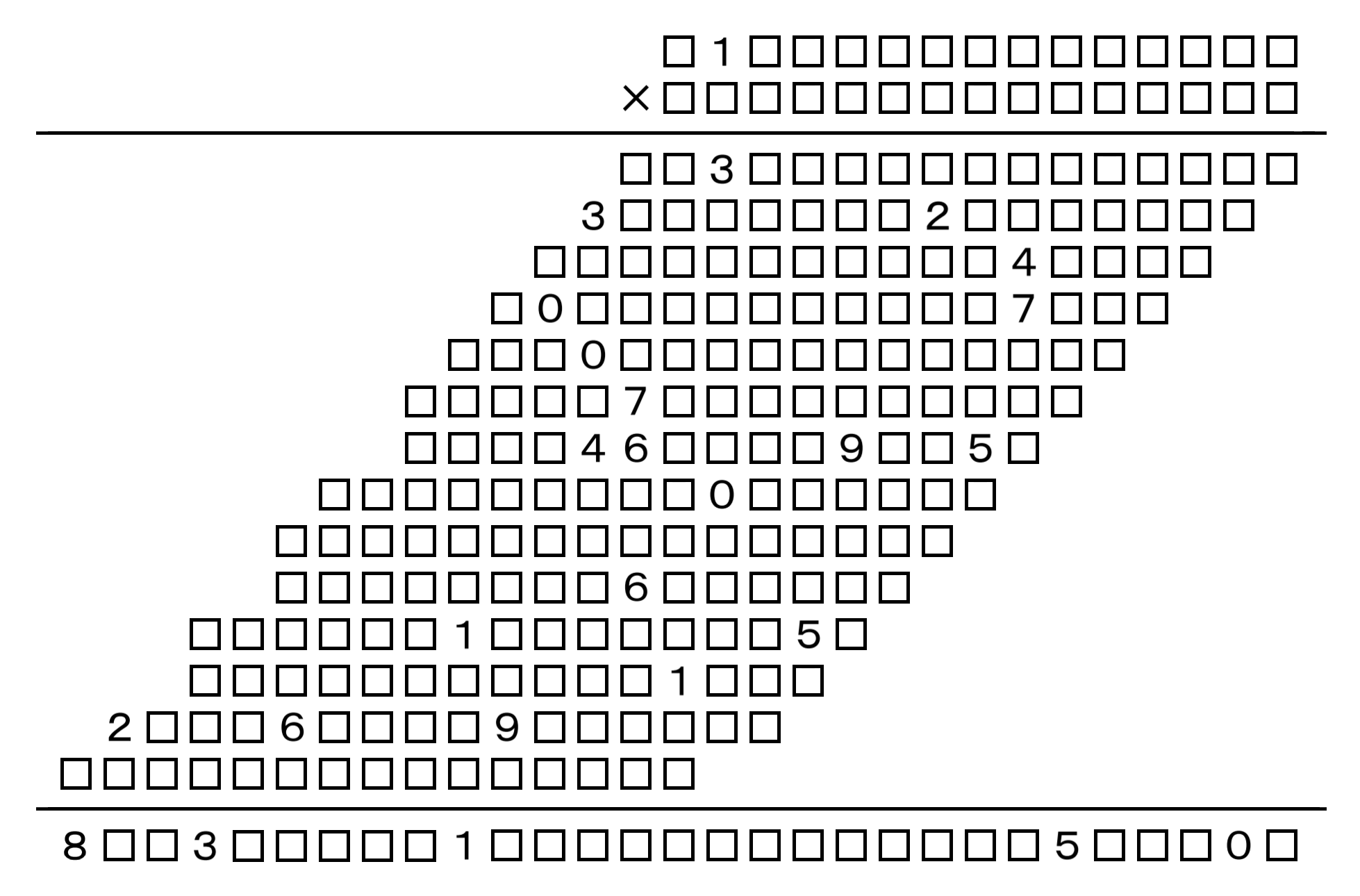
Proponuję coś prostszego, choć niekoniecznie prostego – dwa szkielety silnie spokrewnione, bo mniejszy jest jakby kawałkiem większego. W obu ujawnione są wszystkie jedynki. Szukamy iloczynów.

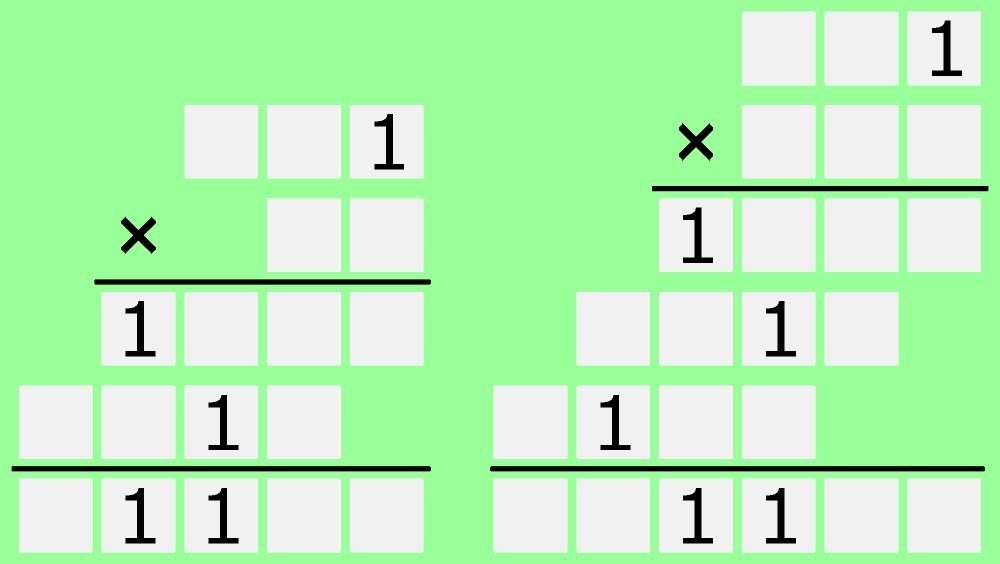
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.