Od 14 do 24

Ile co najmniej pól szachownicy (8×8) należy zablokować (uczynić nieprzechodnimi), aby pozostałe można było obejść wieżą po jedynej możliwej trasie zamkniętej? To pytanie dotyczy tzw. unikalnych cykli wieżowych (UCW), które były tematem artykułu w sierpniowym Świecie Nauki. Z tym tematem wiązało się także zadanie autorstwa apartado, zamieszczone w poprzednim wpisie. Na diagramie tego zadania pojawia się w trakcie rozwiązania poniższy UCW.

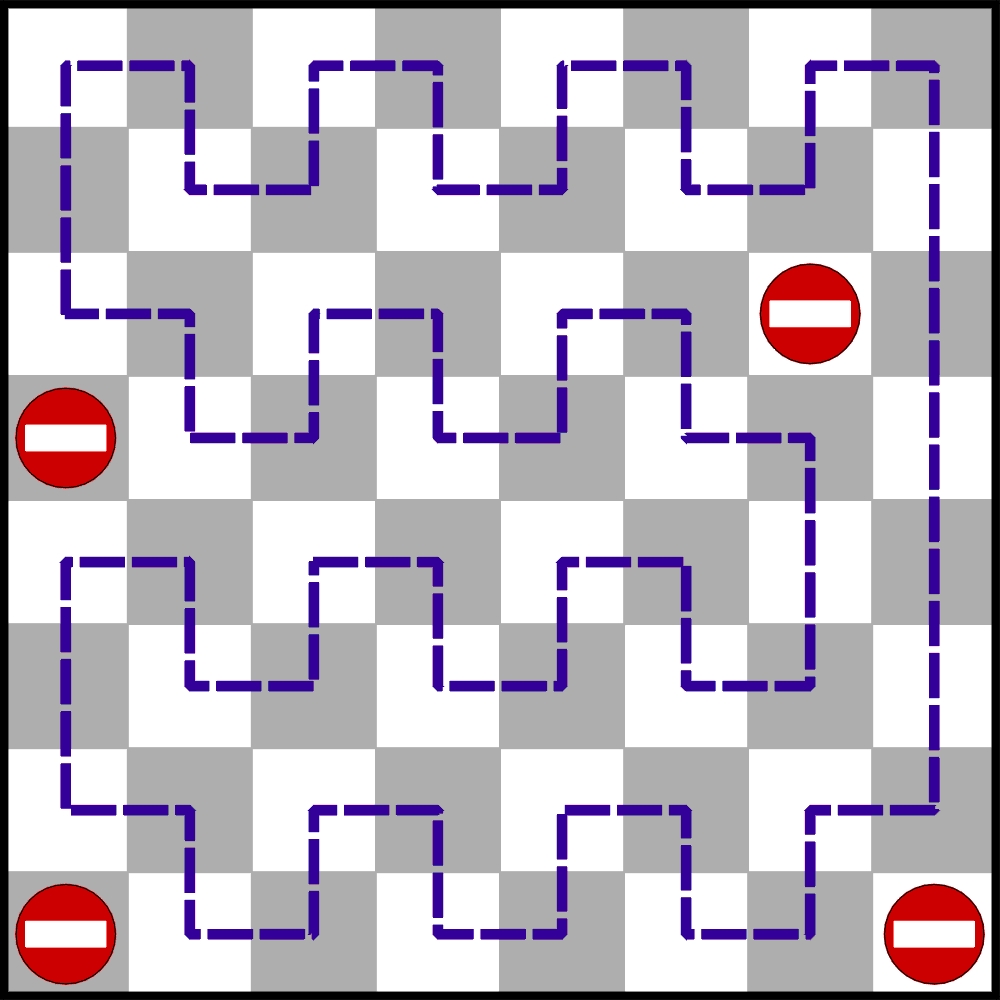
Ten diagram z jedynym możliwym cyklem jest równocześnie odpowiedzią na powyższe pytanie: wystarczą 4 blokady. Takiego rozmieszczenia 4 blokad z UCW, jak na powyższym rysunku, brak jednak wśród kompletu 14 zaprezentowanych we wspomnianym artykule – na co zwrócił uwagę Andrzej111. W artykule jest jednak wzmianka, że nie ma pewności, czy te 14 ustawień to wszystkie – i okazało się, że istotnie nie wszystkie.
A teraz najlepsze. Pisząc o rzekomym komplecie 14 ustawień korzystałem z angielskich źródeł, zapominając o… polskich. Moja niepamięć wydaje się jednak usprawiedliwiona, bo temat blokad gościł w Łamiblogu przed 15 laty i wówczas w komentarzach Antyp zamieścił zestaw – bagatela – 24 różnych ustawień 4 blokad na szachownicy 8×8, dających UCW . Czy to już wszystkie? Nie wiadomo. Proponuję coś prostszego, ale też chyba dla programistów, bo „na piechotę”, czyli bez wsparcia komputerowego raczej nie do ruszenia, a przynajmniej zbyt żmudne.
Liczby całkowicie różnych (z dokładnością do obrotów i odbić lustrzanych) sposobów rozmieszczenia minimalnej liczby blokad na najmniejszych szachownicach, zapewniających UCW, wynoszą:

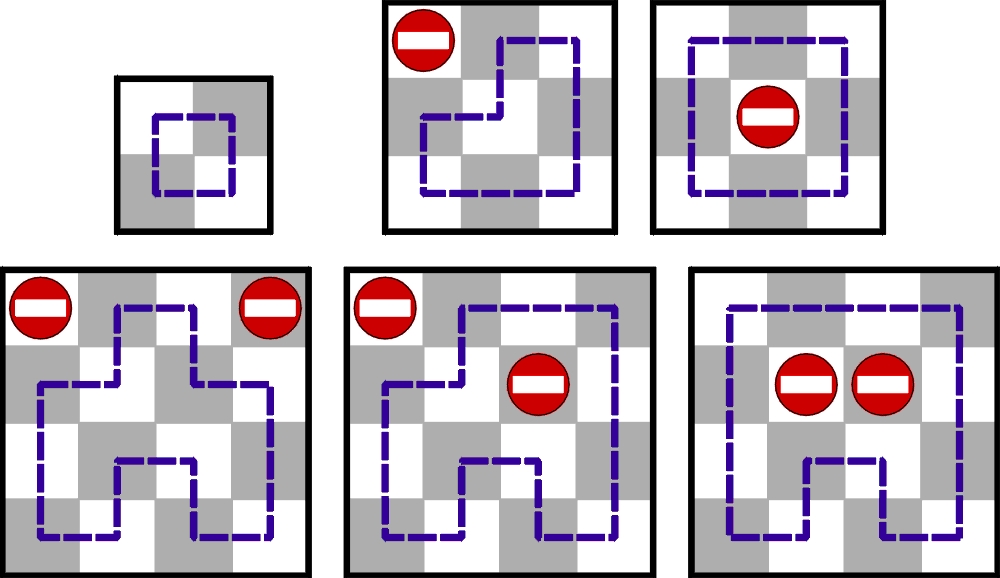
2×2 – 0 blokad – 1 sposób (brak sposobu to też sposób)
3×3 – 1 blokada – 2 sposoby
4×4 – 2 blokady – 3 sposoby
5×5 – 3 blokady – ? sposob(y)(ów)
Jaką liczbą należy zastąpić znak zapytania?

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze

[apartado]

Jestem pewien, że w wolnych chwilach komputer HAL dzieli swoje procesory na dwóch graczy i delektuje się grą o następujących zasadach:

Na szachownicy 8×8 rozmieszczamy 4 figury szachowe (po dwie w kolorach czarny/biały) i wykonujemy nimi na przemian posunięcia.
Celem gry jest spowodowanie żeby przeciwnik ułożył jeden z układów „blokujących” / tworzących UCW wśród wolnych pól.
Trudność mogłaby sprawiać kwestia symetrii wszelakich, ale przecież dla HALa to nie jest problem.

Niuansów nie znam – proszę pytać HALa.

[Antyp1958]

Znalazłem 12 układów

= = o = = = = o = = = = o = = = = o = = = = = = = = = = = =
= = o = = = = = = = = = = = = = = = = = = o o = = = o = = =
= = o = = = o = = = = = o = = = = = = = = = o = = = = o o =
= = = = = = = = o = = = o = = = o o = = = = = = = = = = = =
= = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

o = = = = o = = = = o = = = = o = = = = = = o = = = = o = =
= = o = = = = o = = = = = = = = = = = = = = = = = = = o = =
= = o = = = = = = = = = o o = = = = o = = o o = = = = = = =
= = = = = = = = = = = = = = = = = = = = = = = = = = = = = =
= = = = = = = o = = = = = = = = = o = = = = = = = = = o = =

[Antyp1958]

W poprzednim komentarzu pozżerało mi spacje.

= = o = =/= = o = =/= = o = =/= = o = =/= = = = =/= = = = =
= = o = =/= = = = =/= = = = =/= = = = =/= o o = =/= o = = =
= = o = =/= o = = =/= = o = =/= = = = =/= = o = =/= = o o =
= = = = =/= = = o =/= = o = =/= o o = =/= = = = =/= = = = =
= = = = =/= = = = =/= = = = =/= = = = =/= = = = =/= = = = =

o = = = =/o = = = =/o = = = =/o = = = =/= = o = =/= = o = =
= = o = =/= = o = =/= = = = =/= = = = =/= = = = =/= = o = =
= = o = =/= = = = =/= = o o =/= = = o =/= o o = =/= = = = =
= = = = =/= = = = =/= = = = =/= = = = =/= = = = =/= = = = =
= = = = =/= = o = =/= = = = =/= = o = =/= = = = =/= = o = =

[apartado]

Ciekawe jak bardzo się pomylę:
W miejscu znaku zapytania powinna się znaleźć liczba będąca wynikiem mnożenia liczby 7 oraz liczby poprawnych odpowiedzi w komentarzach.

Jeśli nie będzie problemu z ustaleniem poprawnej odpowiedzi, to pomyłka będzie niewielka.
mp

[Spytko z Melsztyna]

W międzyczasie wrzucam informację dotyczącą wpisu z 10 sierpnia Bezkwadratowo.
Trzecie zadanie, mrówcze, z podziałem na trzy grupy. Udało mi się znaleźć rozbicie zbioru [1,…,85]. Szczegóły w w/w wpisie.

[bubka111]

Wyszło mi 12 po batalii z kompjuterem (mam nadzieję że poprawnie)

[1, 0, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]

[1, 0, 0, 0, 0]
[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 1, 0, 0]]

[1, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 1, 1, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]

[1, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 0, 0],
[0, 0, 1, 0, 0]

[0, 0, 1, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]

[0, 0, 1, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 1, 0, 0]

[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0],
[0, 1, 1, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]

[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 0, 0]

[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0]

[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 1, 1, 0, 0],
[0, 0, 0, 0, 0]

[0, 0, 0, 0, 0],
[0, 1, 1, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]

[0, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 1, 1, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]

Dziwnie mi te wartości przypominają ten ciąg przesunięty o 1
ale nie wiem

https://oeis.org/A307957

[uch_ty]

5×5 – 3 blokady – 13 sposobów.

A wśród nich dwupak
0-0-x-0-0
0-0-0-0-0
0-0-0-x-0
0-0-0-0-0
0-0-x-0-0

[Antyp1958]

Dwupak ma niestety dwa rozwiązania. Symetryczne .