Nie(sk)ładnie
Ten wpis został zainspirowany komentarzem Andrzeja111, dotyczącym pierwszego z zadań zatytułowanych „Nieskładnie”, zamieszczonych w bieżącym Omnibusie.
Diagram zadania jest kwadratem 5×5:
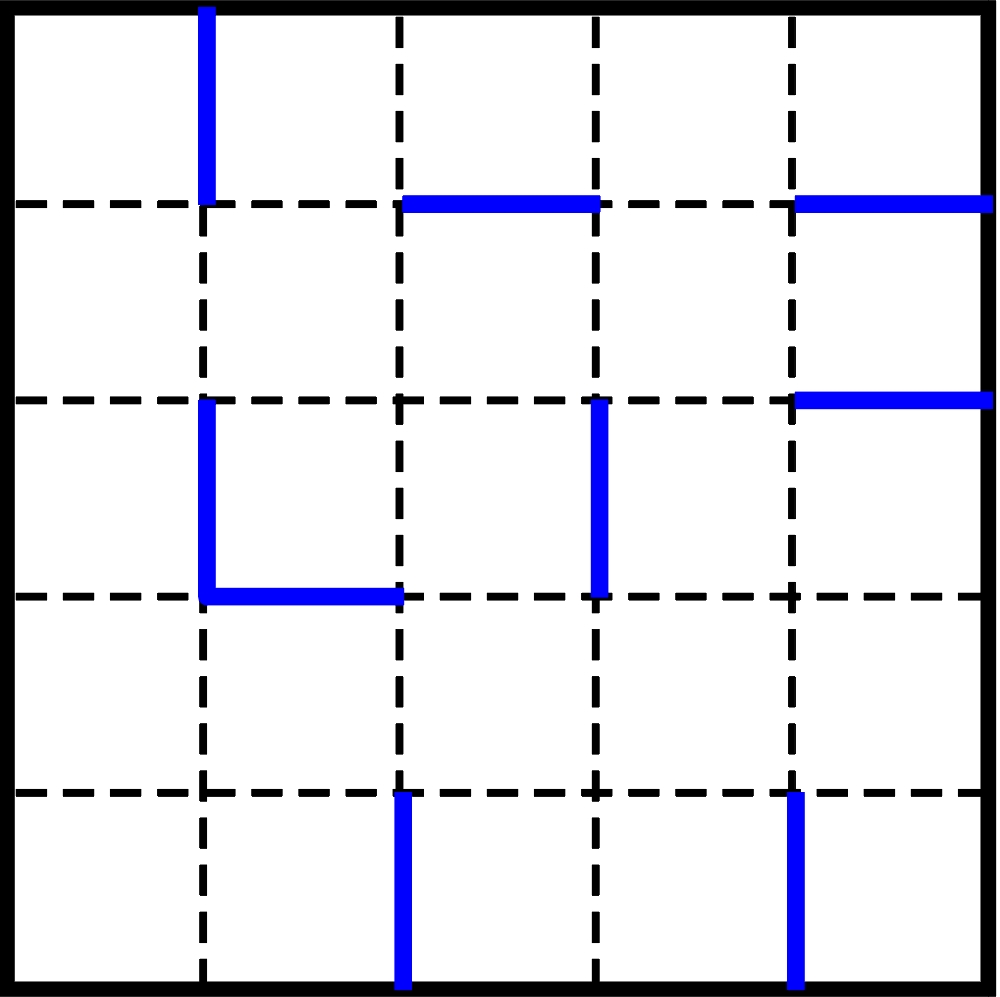
Kwadrat ten należy podzielić wzdłuż linii przerywanych na prostokąty. Niektóre fragmenty linii dzielących (niebieskie) ujawniono. Pozostałe należy poprowadzić tak, aby w dokonanym podziale żadne dwa sąsiednie prostokąty nie tworzyły większego prostokąta.
W Omnibusie podane jest jedno rozwiązanie, ale Andrzej111 słusznie zauważył, że nie jest ono jedynym. Ile więc jest rozwiązań? – oto jest pytanie.
A przy okazji pojawił się ciekawy problem z zakresu geometrii dyskretnej, którym – o ile mi wiadomo – nikt dotąd się nie zajmował. Można go sformułować tak:
Ile jest sposobów podziału (p) kwadratu n×n (złożonego z n^2 kratek) na prostokąty tak, aby żadne dwa lub więcej z tych prostokątów (poza wszystkimi, czyli całym kwadratem) nie tworzyły większego prostokąta?
Dla n<3 p=0, dla n=3 p=1 (kratka otoczona trzema prostokątami 1×2). Szukanie p dla n=5 jest bardzo żmudne, ale z odpowiedzią na pytanie o p dla n=4 nie powinno być kłopotu.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Znalazłam trzy podziały podanego kwadratu 5×5, a cztery podziały kwadratu 4×4
W linku dwa rozwiązania.
https://zapodaj.net/plik-EKbb4xl3Vd
Czy takie znalazł Andrzej111 ?
1)
1 , 2 , 2 , 2 , 2
1 , 3 , 4 , 4 , 4
1 , 3 , 5 , 6 , 6
0 , 0 , 5 , 7 , 8
0 , 0 , 9 , 9 , 8
1 , 2 , 2 , 2 , 2
1 , 3 , 5 , 4 , 4
1 , 3 , 5 , 6 , 7
0 , 0 , 5 , 6 , 7
0 , 0 , 8 , 8 , 7
1 , 2 , 2 , 2 , 2
1 , 3 , 3 , 4 , 4
1 , 3 , 3 , 6 , 7
0 , 0 , 5 , 6 , 7
0 , 0 , 8 , 8 , 7
1 , 2 , 2 , 2 , 2
1 , 3 , 3 , 4 , 4
1 , 3 , 3 , 6 , 7
1 , 0 , 5 , 6 , 7
1 , 0 , 8 , 8 , 7
2)
1 , 1 , 1 , 2
3 , 5 , 5 , 2
3 , 5 , 5 , 2
3 , 4 , 4 , 4
1 , 1 , 2 , 2
3 , 4 , 2 , 2
3 , 5 , 5 , 7
6 , 6 , 6 , 7
2 , 1 , 1 , 1
2 , 1 , 1 , 1
2 , 4 , 4 , 3
5 , 5 , 5 , 3
Logi, jaki jest czwarty?
W Omnibusie są jeszcze dwa większe zadania z tego rodzaju o rozmiarach 6×6, 7×7.
W naturalny sposób powstaje pytanie:
Czy one także mają więcej niż jedno rozwiązanie ?
@logi
Czy można poprosić o ten trzeci podział – zakładam, że dwa moje z linka są wśród tych trzech ?
1)
Dwa lub pięć?
W moim rozwiązaniu zabrakło ułożenia zamieszczonego przez Apartado
1 , 2 , 2 , 2 , 2
1 , 3 , 3 , 4 , 4
1 , 3 , 3 , 5 , 7
1 , 0 , 6 , 6 , 7
8 , 8 , 6 , 6 , 7
Wydaje mi się, że różnice (2 lub 5) wiążą się z kluczowymi słowami,
dla 1): „Aby żadne dwa sąsiednie prostokąty nie tworzyły większego prostokąta”,
dla 2): „Aby żadne dwa lub więcej z tych prostokątów (poza wszystkimi, czyli całym kwadratem) nie tworzyły większego prostokąta”.
14444
13588
13579
22579
22669
to jest rozwiązanie umieszczone w Omnibusie. ( Też trzeba je wziąć pod uwagę? )
1144
2344
2555
2555
oraz
1166
2366
2357
2447
a nie miałam
1122
3422
3557
6667, czyli jest 5 rozwiązań
I jak tu się połapać? Myślę, że ktoś kto tego nie robił nawet nie ma ochoty analizować błędów i przejęzyczeń. Dlatego poniżej podsumuję stan na chwilę obecną, bo nie wykluczam, że ktoś coś dorzuci, a i nie mam pewności czy się nie mylę.
1)
5×5
Odpowiedź: trzy ( żadne dwa lub więcej).
Odpowiedź: pięć (żadne dwa sąsiednie).
Nie mam Omnibusa i nie wiem co tam jest napisane, opieram się wyłącznie na Łamiblogu. Być może w Omnibusie użyte sformułowania preferują wybór: „trzy”. Ale byłbym ciekaw, czy mój wybór „pięć” jest błędny?
Czy Omnibusa można zamówić w wersji cyfrowej?
2)
4×4
Odpowiedź: cztery (żadne dwa sąsiednie lub więcej).
Logi, cztery! Czwarty zawiera 2×2 + 2×3.
Opisane przez Ciebie „oraz”, „nie miałam” są tożsame przez symetrię względem przekątnej rosnącej (w mojej trójce – drugi).
Tak, cztery. Mój błąd