7 hetmanów

13 lipca 2024
Marek Penszko

Nie jestem miłośnikiem łamigłówek wielochodowych, ale to nie powód, żeby się czasem w Łamiblogu nie pojawiały – zwłaszcza jeśli wielo- oznacza nie więcej niż kilkunasto-, choć dla mnie to i tak za dużo.
Wielochodówki kojarzą się oczywiście z szachami i zdarzają się wśród nich kilkunasto-, ale taka liczba to sport umysłowy ekstremalny dla garstki koneserów. Moje szare komórki porywają się najwyżej na trzy-, a na mistrzostwach świata w rozwiązywaniu zadań szachowych granicą jest zwykle siedmio-.
Poza szachami wielochodówki są najczęściej tzw. przesuwankami, w których zaczynając od jakiegoś ustawienia iluś elementów, należy doprowadzić w minimalnej liczbie ruchów do innego, konkretnego ustawienia. Oto przykład, formalnie jakby szachowy.
Na szachownicy stoi siedem hetmanów – trzy czarne na lewej połowie planszy i cztery białe na prawej.

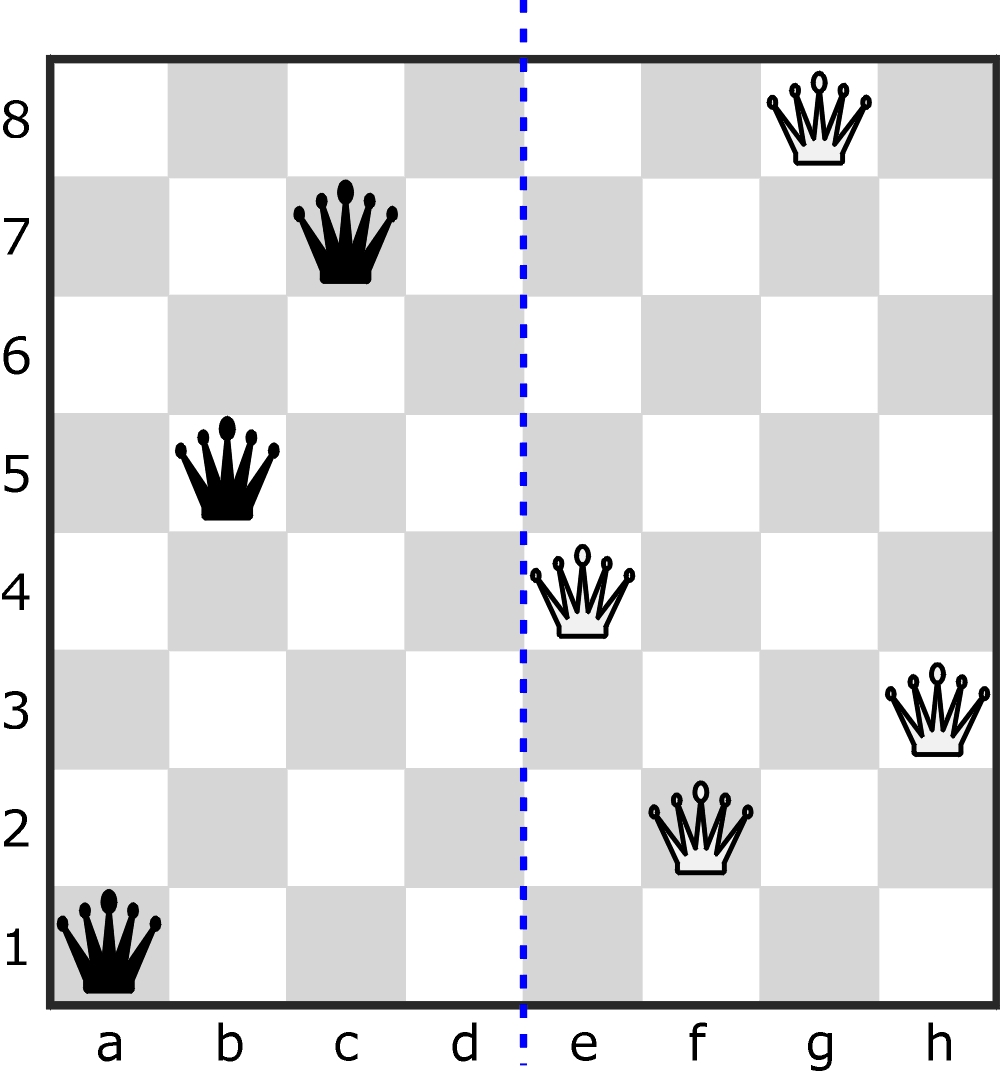
Zadanie polega na wykonaniu nimi jak najmniejszej liczby ruchów tak, aby wszystkie czarne znalazły się na prawej połowie, a wszystkie białe na lewej. Jest tylko jeden kluczowy warunek: żaden hetman po ruchu nie może trafić na pole atakowane przez innego hetmana. Warunek ten nie jest związany z kolorami hetmanów, tzn. biały nie może się także znaleźć na polu atakowanym przez innego białego – i podobnie w przypadku czarnych. Kolejność wykonywania ruchów jest niezależna od koloru figur (niekoniecznie na przemian białe i czarne). Jak porusza się hetman – każdy wie.
Zadanie nie wydaje się zbyt trudne, ale dość żmudne, więc zdecydowanie dla wytrwałych – choćby dlatego, że zapewne konieczne jest skorzystanie z szachowych rekwizytów.

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.