Hetmandoku
Problem ośmiu hetmanów należy do sztandarowych w tzw. matematyce szachowej. Przypomnę, że chodzi o rozmieszczenie na szachownicy (8×8) ośmiu hetmanów tak, aby żaden z nich nie atakował żadnego z pozostałych. Zadanie liczy sobie 175 lat i zostało rozgryzione do imentu także w wersji uogólnionej dla n hetmanów na planszy n×n.
Serbski główkołamacz i szachista Nikola Zivanovic sprytnie pożenił ten szachowy problem z sudoku, a ściślej z sudokowym wariantem 8×8.
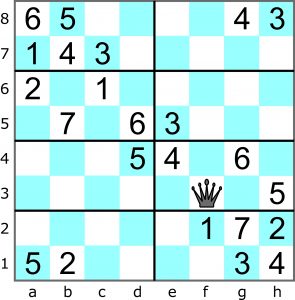
W każdym wierszu, kolumnie oraz w ograniczonym grubszą linią prostokącie 4×2 powinno się znaleźć siedem różnych cyfr (od 1 do 7) oraz hetman. Obowiązuje dodatkowa zasada związana ze wspomnianym wyżej problemem, czyli hetmany nie mogą się atakować.
W rozwiązaniu wystarczy podać pozycje hetmanów.
Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze
Pozycje hetmanów można ustalić dość szybko, kiedy jeszcze sporo cyfr zostaje do wpisania: a4, b2, c8, d6, e1, f3, g5, h7.
a4,b2,c8,d6,e1,f3,g5,h7
Wstęp do analizy analizy:
Początek to było uzupełnienie brakujących Hetmanów.
(zajmują one 18% początkowo wolnych pól a poświęciłem na to 39% całego czasu rozwiązywania).
Zadanie sprowadza się do rozwiązania zwykłego sudoku (gdzie ósemka to hetman)
Następnie sprawdzamy warunek dodatkowy, czyli hetmany nie mogą się atakować.
Wynik
65X21743
1437652X
231X7456
475632X1
X1254367
76432X15
3X645172
5271X634
Zadanie robi się znacznie ciekawsze (trudniejsze) jeżeli pozycja hetmana (f3) nie jest zadana
Rozwiązanie dalej pozostaje jedno.
Dzisiaj proste:
a4, b2, c8, d6, e1, f3, g5, h7.
1e
2b
3f
4a
5g
6d
7h
8c
Hetmany: a4, b2, c8, d6, e1, f3, g5, h7
Pytanie za łatwe, bo do odnalezienia pozycji hetmanów można zacząć i nie trzeba rozwiązywać całości (a nawet połowy).
1e, 2b, 3f, 4a, 5g, 6d, 7h, 8c
PS Na poprzednią zagadkę też wysłałam odpowiedź, ale zaginęła (?).
Pani Olu, nie zaginęła tylko ją usunąłem, bo składała się tylko z kropki (teraz przywróciłem tę komentarzokropkę).
mp
No to tak:
65H21743
1437652H
231H7456
475632H1
H1254367
76432H15
3H645172
5271H634
Zwolennik prawdy zawsze zaczyna od ujawnienia prowodyrów.
W przeciwnym razie pozostaje droga przez „maszynkę”,
aby na końcu o mały włos nie pominąć pokojowego warunku.
c8,h7,d6,g5,a4,f3,b2,e1 – tak
c8,h7,b6,g5,a4,f3,d2,e1 – nie
No trudno, wysyłałam ją bardzo późno wieczorem, widocznie coś poszło nie tak 🙂
E1, B2, F3, A4, G5, D6, H7, C8
C8, g7, d6, h5, b4 f3, a2, e1
Trochę dobrze, trochę źle
mp
Wykorzystując to forum, chciałem wszystkim polecić fantastyczny wywiad z panem Markiem we wrześniowym Świecie Nauki. Znajdują się tam odpowiedzi na wiele pytań, które sam chciałem zadać.
A Panu Markowi serdecznie gratuluję „okrągłej” rocznicy i życzę kolejnych!
Powiedział Pan takie zdanie: „[…] tempo życia nie sprzyja skupianiu się nad jakimś ciekawym, ale niekoniecznie prostym zagadnieniem lub zadaniem”. Na pewno tak, ale też wiele osób, które mają łamigłówkowe inklinacje, a które kiedyś zajęłyby się np. szachami, dziś wieczorami pracuje nad różnymi osobistymi przedsięwzięciami np. w pythonie. Ten świat też jest fascynujący, tylko w trochę inny sposób.
Dziękuję za „reklamę”:)
mp